2. Построение типовой модели

Пример:

По 20 предприятиям региона изучается зависимость производительности труда У (выработки на одного работника, тыс. руб.) от ввода в действие новых основных фондов Х1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих Х2 (%).

Таблица 3.1 – Исходные данные

Предприятие, №	Выработки на одного работника, тыс. руб. (У)	Ввод в действие новых основных фондов, % (Х1)	Удельный вес рабочих высокой квалификации в общей численности рабочих, % (Х2)
1	12	5,9	11
2	12	5,9	15
3	12	5,7	16
4	12	6	17
5	12	5,8	18
6	12	6,8	20
7	13	7,4	20
8	13	6,4	21
9	13	7,3	21
10	15	8,8	21
11	14	8	22
12	16	8,4	23
13	14	8,8	23
14	16	9,2	26
15	17	10	29
16	17	10,2	30
17	17	10,1	31
18	17	10,5	32
19	19	11,6	33
20	19	11	37

Требуется:

1. Проверить характер распределения каждого признака и сделать выводы о возможности применении МНК для построения регрессионной модели.

2. Построить матрицу парных линейных коэффициентов корреляции, сделать соответствующие выводы.

3. Оценить параметры уравнения множественной регрессии и, дать им экономическую интерпретацию.

4. Построить уравнение множественной регрессии в стандартизованном масштабе. Рассчитать показатели тесноты многофакторной связи.

5. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.

6. С помощью F-критерия Фишера оценить статистическую надежность уравнения множественной регрессии и показателя тесноты связи. Сравнить значение скорректированного и нескорректированного коэффициента множественной детерминации. Оценить системный эффект многофакторной модели.

7. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора Х1 по сле Х2 и фактора Х2 после Х1.

8. Оценить с помощью t-критерия Стьюдента значимость коэффициентов «условно чистой» регрессии.

9. Рассчитать прогноз значения результативного признака, при прогнозном значении факторных показателей, составляющим 150% от их среднего уровня.

Решение:

1. Проверим характер распределения признаков, для рассчитаем описательную статистику для каждого из признаков с помощью ППП MS Excel (методика расчета рассмотрена в Разделе 1):

Таблица 3.2. – описательная статистика

Показатель	У	Х1	Х2
Среднее	14,6	8,19	23,3
Стандартная ошибка	0,54964	0,433523	1,52367
Медиана	14	8,2	21,5
Мода	12	5,9	21
Стандартное отклонение	2,45807	1,938773	6,81407
Дисперсия выборки	6,04211	3,758842	46,4316
Эксцесс	-1,1961	-1,33143	-0,53653
Асимметричность	0,4451	0,188101	0,3278
Интервал	7	5,9	26
Минимум	12	5,7	11
Максимум	19	11,6	37
Сумма	292	163,8	466
Счет	20	20	20
Уровень надежности(95,0%)	1,15041	0,907374	3,18908

Рассчитаем коэффициенты вариации для каждого из признаков:

; .

;

.

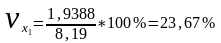Так как коэффициенты вариации по каждому из признаков не превышают порогового значения 35 %, то можно сделать вывод о том, что распределение по каждому из признаков однородно.

Рассчитанные выше показатели асимметрии позволяют сделать вывод, что по каждому из признаков наблюдается незначительная правосторонняя асимметрия. Эксцесс слабый отрицательный. Таким образом, описательная статистика позволяет заключить, что распределение по каждому из признаков подчиняется нормальному закону, следователь выборочные данные модельных признаков возможно использовать для построения регрессионной модели.

2. Построим матрицу парных линейных коэффициентов корреляции, для этого обратимся к расчетной таблице 3.3

Таблица 3.3. – Расчетные данные необходимые для вычисления парных коэффициентов корреляции

1	70,8	132	64,9
2	70,8	180	88,5
…	…	…	…
19	220,4	627	382,8
20	209	703	407
Итого	2479,3	7103	4053,2
Среднее значение	123,965	355,15	202,66

Рассчитаем парные линейные коэффициенты корреляции:

;

;

.

Построим матрицу парных линейных коэффициентов корреляции:

Таблица 3.4 – Матрица парных линейных коэффициентов корреляции

Признаки
	1	0,9699	0,9408
	0,9699	1	0,9428
	0,9408	0,9428	1

Значения рассчитанных коэффициентов парной линейной корреляции позволяют сделать вывод о наличии очень тесной связи между факторами и результативным признаком. Одна следует выделить и высокую межфакторную связь, которая свидетельствует о наличии коллениарности факторов, поэтому фактор можно исключать из модели, ввиду менее тесной связи его с результативным показателем.

3. Построим уравнение множественной регрессии. Для определения коэффициентов условно чистой регрессии построим систему нормальных уравнений:

Где:

i – номер наблюдения,

j – номер фактора.

Для решения системы нормальных уравнений построим расчетную таблицу 3.5.

Таблица 3.5. – Расчет параметров уравнения множественной регрессии и корреляции

№
1	-2,29	-12,3	-2,6	5,2441	151,29	5,954	31,98	28,167
2	-2,29	-8,3	-2,6	5,2441	68,89	5,954	21,58	19,007
…	…	…	…	…	…	…	…	…
4	-2,19	-6,3	-2,6	4,7961	39,69	5,694	16,38	13,797
20	2,81	13,7	4,4	7,8961	187,69	12,364	60,28	38,497
å	-	-	-	71,418	882,2	87,82	299,4	236,66

Подставим в систему нормальных уравнений из таблицы 3.5. необходимые расчетные величины, получим систему:

Решаем систему:

Определим свободный член уравнения:

Таким образом, получаем общий вид уравнения множественной регрессии и корреляции:

Коэффициенты условно чистой регрессии, т.е. b_j являются именованными числами, выраженными в различных единицах измерения, в тех же единицах, что и соответствующие им факторы. Поэтому они не сравнимы друг с другом, т.е. по их величине нельзя сделать вывод, какой из факторов в наибольшей степени влияет на результат. Для приведения их в сравнимый вид применяется то же преобразование, что и для получения парных коэффициентов. Полученную величину называют стандартизированным коэффициентом регрессии.

4. Построим уравнение множественной регрессии в стандартизованном масштабе. Рассчитаем показатели тесноты многофакторной связи.

   1. Построим уравнение множественной регрессии в стандартизованном масштабе:

Определим бета-коэффициенты:

;

Тогда уравнение регрессии в стандартизированном масштабе имеет вид:

Полученное уравнение регрессии в стандартизированном масштабе, позволяет сделать вывод о том, что наибольшее влияние на уровень производительности труда оказывает первый фактор – коэффициент обновления основных фондов, поскольку

2. Рассчитаем множественный коэффициент корреляции и детерминации:

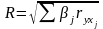
Множественный коэффициент корреляции позволяет судить о достаточно сильной связи факторов с результативным признаком.

Рассчитаем множественный коэффициент детерминации:

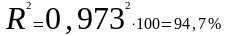
Согласно рассчитанного множественного коэффициента детерминации, вариация (изменение) производительности труда на 94,7 % обусловлена изменением уровня ввода новых основных фондов и удельного веса рабочих высокой квалификации в общей численности рабочих.

3. Рассчитаем коэффициенты частной корреляции:

Коэффициенты частной корреляции дают более точную оценку тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очищают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели.

Рассчитанные коэффициенты частной регрессии, позволяют сделать следующий вывод. Если сравнивать коэффициенты парной и частной корреляции, то можно заметить, что из-за высокой межфактороной связи коэффициенты парной корреляции дают завышенные оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной коллениарности факторов исключить из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи, в данном случае это фактор .

5. Рассчитаем средние частные коэффициенты эластичности:

Средние частные коэффициенты эластичности показывают, на сколько процентов от значения своей средней величины изменяется результат при изменении фактора на 1 % от своей средней, при фиксированном воздействии на результат всех прочих факторов, включенных в модель.

Средние частные коэффициенты эластичности позволяют сделать вывод:

- при изменении фактора на 1% от своего среднего значения, результативный признак у измениться в среднем на 0,53% от своего среднего уровня;

- при изменении фактора на 1% от своего среднего значения, результативный признак у измениться в среднем на 0,14% от своего среднего уровня;

Таким образом, еще раз подтверждаем, что наибольшее влияние на результативный показатель у оказывает фактор .

6. С помощью F-критерия Фишера оценим статистическую надежность уравнения множественной регрессии и показателя тесноты связи. Сравним значение скорректированного и нескорректированного коэффициента множественной детерминации. Оценим системный эффект многофакторной модели.

6.1. С помощью F-критерия Фишера оценим статистическую надежность уравнения множественной регрессии и показателя тесноты связи.

Выдвигаем нулевую гипотезу о статистической не значимости уравнения множественной регрессии и показателя тесноты многофакторной связи.

Рассчитаем фактический уровень F-критерия:

и

Так как 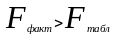, отклоняем нулевую гипотезу и делаем вывод о том, что в вероятность 95% уравнение множественной регрессии и показатель тесноты многофакторной связи статистически значимы и надежны.

6.2. Сравним значение скорректированного и нескорректированного коэффициента множественной детерминации.

Сравнивая корректируемый и некорректируемый коэффициенты множественной детерминации, приходим к выводу, что они практически не отличаются, следовательно, можно утверждать о неплохом качестве построенной модели.

Оценить системный эффект многофакторной модели.

6.3. Оценим системный эффект многофакторной модели.

Системный эффект достаточно велик, следователь утверждаем о хорошей совместимости факторов, вероятно в данном случае это связано с высокой межфакторной связью.

7. С помощью частных F-критериев Фишера оценим целесообразность включения в уравнение множественной регрессии фактора после и фактора после _.

_{Выдвигаем гипотезу о несущественности прироста за счет дополнительного включения фактора.}

Критический уровень для частных показателей F-критерия составит:

Рассчитанные частные F-критерии Фишера позволяют сделать следующие выводы:

- так как > , то нулевая гипотеза отвергается, включение первого фактора после второго целесообразно и обоснованно, поскольку его включение существенно увеличивает долю факторной дисперсии.

- так как < , то нулевая гипотеза принимается, включение второго фактора после первого не целесообразно и не обоснованно, поскольку его включение существенно не увеличивает долю факторной дисперсии. Поэтому парная регрессия зависимости производительности труда от коэффициента обновления основных фондов является достаточно статистически значимой, надежной и нет необходимости улучшить ее, включая дополнительный фактор _.

8. Оценим с помощью t-критерия Стьюдента значимость коэффициентов «условно чистой» регрессии. Суть оценки сводиться к сравнению коэффициентов с их ошибкой, расчет которых достаточно затруднителен. Более простой способ расчета t-критерия Стьюдента для коэффициентов регрессии линейного уравнения как квадратного корня из соответствующего частного F-критерия Фишера:

Критический уровень для t-статистики Стьюдента составит:

Сравнивая критический (табличный) уровень t-статистики с фактическим, приходим к выводу о том, что так как 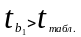коэффициент регрессии является статистически значимым и надежным, на него можно опираться в анализе и прогнозе. Так как

делаем вывод о том, что коэффициент регрессии является статистически незначимым и не надежным, поскольку он имеет случайный характер формирования.

Таким образом, еще раз убеждаемся в обоснованности включения в модель первого фактора – коэффициента обновления основных фондов и не существенности включения второго – квалификации рабочих. Построение многофакторной модели нецелесообразно, достаточно построить линейную модель парной корреляции и регрессии с одним факторным признаком.

9. Рассчитаем прогнозное значение результативного признака, при прогнозном значении факторных показателей, составляющим 150% от их среднего уровня.

По условию прогнозное значение факторов составит:

;

.

Подставив прогнозное значение факторов в уравнение множественной регрессии, получим точечный прогноз результативного признака:

Для расчета интервального прогноза результативного признака, следует использовать величину средней квадратической ошибки аппроксимации, которая вычисляется по формуле:

Следовательно, с вероятностью 0,68 прогнозируемая производительность труда составит: ,

а с большей надежностью 0,95 составит:

или от 18,29 до 20,69 тыс.руб.

Данный расчет относиться к прогнозу производительности труда для отдельных предприятий. Расчет интервального прогноза производительности для совокупности 20 предприятий составит:

Интерпретация этого значения ошибки прогноза средней величины такова: если обеспечить 20 предприятий значением факторов 12,29% и 34,95% соответственно, то с вероятностью 0,95 средняя по совокупности предприятий производительность труда составила бы , или от 19,36 до 19,62 тыс.руб.