2.3.Решение типовых задач с помощью ппп ms Excel и Statistica 6.1
Построение однофакторных корреляционно-регрессионных моделей позволяет пакет прикладных программ MS Excel и Statistica 6.1. Встроенная функция «Регрессия» рассчитывает все необходимые для моделирования параметры уравнения регрессии, а также позволяет оценить статистическую значимость модели по основным существующим критериям оценки статистической надежности модели.
Пример:
А. Рассмотрим построение линейной парной корреляционно-регрессионной модели по исходным данным (таблица ) с помощью ППП MS Excel:
1) Введите исходные данные или откройте существующий файл, содержащий анализируемые данные:
Рисунок 2.3 – Исходные данные для анализа
2) В главном меню последовательно выберем вкладки Данные/Анализ данных/ Регрессия
Рисунок 2.4 – Диалоговое окно Анализ данных
3)Заполните диалоговое окно ввода данных и параметров ввода (рисунок )
Рисунок 2.5 – Диалоговое окно ввода параметров инструмента Регрессия
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал Х – диапазон, содержащий данные факторов независимого признака;
Метки – флажок, который указывает, содержит ли первая строка название столбцов или нет (в данном примере диапазон выделен вместе с названием столбцов)
Константа – нуль – флажок, указывающий на наличие или на отсутствие свободного члена в уравнении (в данном примере определяем параметр а, т.е. флажок не ставим)
Выходной интервал – достаточно указать любую свободную ячейку для будущего итогового диапазона выходных данных
Если необходима подробная информация об остатках, ставим соответствующие флажки в окнах: Остатки, Стандартизированные остатки, График остатков, График подбора, График нормальной вероятности.
Результаты регрессионного анализа для исходного примера представлены на рисунке .
Рисунок 2.6 – Результаты применения инструмента Регрессия
Сравнивая полученные значение с ранее высчитанными в ручном режиме, убеждаемся в правильности расчета
Правильность расчета прогнозного значения результативного признака проверим с помощью встроенной функции Статистические/ТЕНДЕНЦИЯ:
В главном меню последовательно выбираем вкладки Формулы/Другие функции/Статистические/Тенденция (Рисунок )
Рисунок 2.7 – Диалоговое окно инструмента Тенденция
2)Заполните необходимы данные в диалоговом окне (Рисунок )
Рисунок 2.7 – Диалоговое окно ввода аргументов инструмента Тенденция
Известные_значения_у – диапазон, содержащий данные результативного признака;
Известные_значения_х – диапазон, содержащий данные факторов независимого признака;
Новые_значения_х – прогнозируемая величина факторного признака
Константа - логическое значение, которое указывает на наличие или отсутствие свободного члена (константа=1 – свободный член есть; константа=0 свободного члена нет)
Полученное прогнозное значение составило 40,766 т/ч. Сравнивая полученное значение с ранее вычисленным в ручном режиме, убеждаемся в правильности расчета
А. Рассмотрим построение линейной парной корреляционно-регрессионной модели по исходным данным (таблица ) с помощью ППП Statistica 6.1.:
1) Введите исходные данные или откройте существующий файл, содержащий анализируемые данные:
Рисунок 2.8 – Исходные данные для анализа
2) В главном меню последовательно выберем вкладки Анализ/Множественная регрессия/Переменные.
Зависимые переменные – результативный признак;
Независимые переменные – факторный признак.
После обозначения исходных переменных нажимаем ОК.
Рисунок 2.9 – Диалоговое окно ввода переменных
3) При необходимости расчета описательных статистик ставим флажок в строке «Описательные статистики», нажимаем ОК.
Рисунок 2.10 – Диалоговое окно инструмента Регрессия
4) При необходимости расчета выбираем последовательно вкладки в меню описательная статистика
Рисунок 2.11 – Диалоговое окно инструмента Описательная статистика
5) После расчета описательных статистик нажимаем ОК, переходим к Результатам регрессионного анализа:
Рисунок 2.12 – Диалоговое окно результатов использования инструмента Регрессия
6) Нажимаем на вкладку итоговая таблица регрессии - получаем все необходимые параметры и показатели корреляционно-регрессионного анализа:
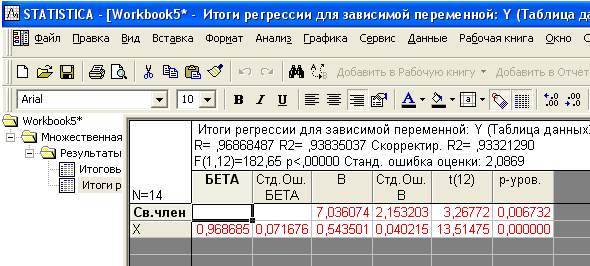
Рисунок 2.13 – Результаты вычисления инструмента Регрессия
В шапке таблицы рассчитаны:
- коэффициент корреляции
- коэффициент детерминации,
- корректированный коэффициент детерминации,
- фактический уровень F-критерия Фишера
- вероятностью ошибки.
Таблица итогов регрессии состоит из шести столбцов где:
БЕТА – стандартизированный коэффициент регрессии
Стд.Ош.БЕТА – ошибка стандартизированного коэффициента
В – параметры уравнения регрессии
Стд.Ош.В – ошибки параметров уравнения регрессии
t- критерий Стьюдента для параметров уравнения регрессии
p – вероятность ошибки оценки параметров.
7) В диалоговом окне Результаты множественной регрессии выбираем вкладку Дисперсионный анализ, получаем таблицу дисперсионного анализа:
Рисунок 2.14 – Диалоговое окно Дисперсионный анализ
8) Для расчета прогнозного значения результативного показателя в диалоговом окне Результаты множественной регрессии выбираем вкладку Предсказать зависимую переменную, в окне Х задаем прогнозное значение факторного признака:
Рисунок 2.15 - Диалоговое окно ввода предсказанных факторных переменных
9) После ввода прогнозируемого значения факторного показателя нажимаем вкладку ОК, выводим прогнозное значение результативного показателя:
Рисунок 2.16 – Результаты применения функции Предсказать зависимую переменную
Сравнивая полученные данные с показателями рассчитанными в ручном режиме убеждаемся в правильности расчетов.
Следует отметить, что в отличии от ППП MS Excel, ППП Statistica 6.1. предоставляет более широкие возможности для моделирования. В частности в программе Statistica 6.1. глубоко рассмотрен корреляционный анализ, анализ остатков регрессии, что представляет широкие возможности для качественного построения модели и соответственно надежного результата при прогнозировании показателей. Существенным отличием программы Statistica от MS Excel, является возможность построения нелинейной формы модели.
А. Рассмотрим построение нелинейной парной корреляционно-регрессионной модели (равносторонней гиперболы) по исходным данным (таблица ) с помощью ППП Statistica 6.1.:
1) Введите исходные данные или откройте существующий файл, содержащий анализируемые данные, последовательно откройте вкладки Анализ/Углубленные методы анализа/Нелинейное оценивание/Регрессия пользователя/Метод наименьших квадратов МНК/Ок.
Рисунок 2.17 – Диалоговое окно инструмента Нелинейное оценивание
Оцениваемая функция – окно предназначенное для ввода нелинейной функции регрессионной модели (в данном примере – равносторонняя гипербола)
2) Нажимаем вкладку ОК, выбираем метод оценивания:
Рисунок 2.18 – Диалоговое окно выбора метода нелинейного оценивания
3) В диалоговом окне Результаты выбираем вкладку Оценки параметров модели, получаем итоговую таблицу регрессионного анализа:
Рисунок 2.19– Результаты применения инструмента Нелинейное оценивание
Таблица итогов регрессии состоит из шести столбцов, где:
Оценка – параметры уравнения нелинейной регрессии;
Стд.Ош.БЕТА – ошибка параметров;
Стд.Ош.В – ошибки параметров уравнения регрессии
t- критерий Стьюдента для параметров уравнения регрессии
p – вероятность ошибки оценки параметров.
Ниж.Дов.Предел - нижний доверительный придел параметров;
Вер.Дов.Предел - верхний доверительный придел параметров;
4) В диалоговом окне Результаты используя инструмент Дисперсионный анализ, получаем таблицу дисперсионного анализа:
Рисунок 2.20 - Диалоговое окно Дисперсионный анализ
5) Для оценки остатков нелинейной регрессионной модели в диалоговом окне Результаты выбираем вкладку Остатки, получаем перечень инструментов необходимых для оценки необъясненной части регрессии:
Рисунок 2.21 – Диалоговое окно функции Остатки инструмента Нелинейное оценивание