Раздел 2

ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ

2.1. Методические указания

Регрессионная модель – это функция, описывающая зависимость между количественными характеристиками социально-экономических систем. Они строятся в тех случаях, когда известно, что зависимость между факторами существует и требуется получить ее математическое описание.

Однофакторная (парная) регрессия представляет собой регрессию между двумя переменными – у и х, т.е. модель, вида:

y = (x),

где у – зависимая переменная (результативный признак);

х – независимая, или объясняющая, переменная (признак-фактор).

Различают линейные и нелинейные регрессии.

Линейная регрессия: y = a+bx+.

Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам:

• полиномы разных степеней y = a+b₁·x+b₂·x²+b₃·x³+e

• равносторонняя гипербола y = a+b/x+e и регрессии, нелинейные по оцениваемым параметрам:

• степенная y = ax^b ·e

• показательная y = a·b^x ·e

• экспоненциальная y = e ^a+b·x ·e

Спецификация модели – формулировки вида модели (выбор вида математической функции, выбор существенных для модели факторов), исходя из соответствующей теории связи между переменными.

В парной регрессии выбор вида математической функции y = (x) может быть осуществлен тремя методами:

-графический,

-аналитический,

- экспериментальный.

Простейшей системой связи является линейная связь между двумя признаками – парная линейная регрессия. Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:

Ŷ = a+bx,

где ŷ – среднее значение результативного признака у при определенном значении факторного признака х;

а – свободный член уравнения;

b – коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения – вариация у, приходящаяся на единицу вариации х.

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют Метод наименьших квадратов (МНК) МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических ŷ минимальна, т.е.

 (y – ŷ)² min

Так как оценка параметров уравнения парной регрессии производится с помощью МНК (метод наименьших квадратов), а данный метод применим только при построении линейной модели, построению нелинейных регрессий предшествует процедура ЛИНЕАРИЗАЦИИ.

Т.е процедура приведения нелинейной модели в линейный вид. В зависимости от вида нелинейной функции модели, существуют два способа линеаризации (анаморфоза):

- способ подстановки (линеаризуются нелинейные регрессии по включенным переменным);

- способ логарифмирования обеих частей уравнения (линеаризуются нелинейные регрессии по оцениваемым параметрам).

Система нормальных уравнений:

n a + b x =  y

a x + b x² =  xy

Можно решить эту систему уравнений по исходным данным или использовать формулы, вытекающие из этой системы:

a =

b= ,

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_xy для линейной регрессии (-1 r_xy 1);

_ИЛИ

Индекс корреляции ρ_xy характеризует силу связи в нелинейной регрессии . (0 ρ_xy 1):

ρ_{xy= .}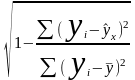

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений результативного признака от фактических:

Допустимый предел значений 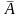– не более 8 – 10%.

Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения:

.

Для линейной регрессии

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:

Правило сложения дисперсий:

å( y_i - )² = å(ŷ_x - )² + å(y_i - ŷ_x)²

где å(y_i - )² – общая сумма квадратов отклонений – общая дисперсия («общая»);

å(ŷ_x - )² – сумма квадратов отклонений, обусловленная регрессией (это объясненная или факторная дисперсия, «регрессия»)

å(y_i - ŷ_x)² – остаточная сумма квадратов отклонений («остаточная»).

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака y характеризует коэффициент (индекс) детерминации R²;

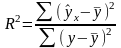ИЛИ

F-критерий – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

Любая сумма квадратов отклонений связана с числом степеней свободы, которое зависит от числа единиц совокупности n и числом определяемых по ней констант (переменных при х )(m).

D_общ= å( y_i - )² / (n-1)

D_факт= å(ŷ_x - )² / m

D_ост= å(y_i - ŷ_x)² /n-m-1

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия:

F = D_факт/D_{ост =}

где F-критерий для проверки нулевой гипотезы Но: D_факт = D_ост.

Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности () наличия нулевой гипотезы (уровень значимости  - вероятность отвергнуть правильную гипотезу при условии, что она верна). Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: F_факт  F_табл – Но отклоняется.

Если эта величина окажется меньше табличного, то вероятность нулевой гипотезы выше заданного уровня (например, 0, 05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной ошибки:

; ;

Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

где S²_ост – остаточная дисперсия на одну степень свободы.

сравнивая фактическое и критическое (табличное) значения t-статистики принимаем или отвергаем гипотезу Но.

Если t_табл  t_факт, то Но отклоняется, т.е. a, b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если t_табл  t_факт, то гипотеза Но не отклоняется и признается случайная природа формирования a, b, r.

Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:

∆a = t_табл m_a,

∆b = t_табл m_b

Доверительные интервалы рассчитываются следующим образом:

=a ± Da =b ± Db;

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значение.

Прогнозное значение результативного признака y_p определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения x_p. Вычисляется средняя стандартная ошибка прогноза

= ,

где .

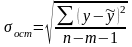Далее строится доверительный интервал прогноза:

;

где