Лабораторная работа №3 Построение силовых линий и эквипотенциальных поверхностей электростатического поля

Цель работы: Построить эквипотенциальные линии электростатического поля для данных электродов, определить направление вектора Е и градиента , определить напряженность электростатического поля.

Сведения из теории

Электрическое поле – одна из форм существования материи, посредством которой осуществляется взаимодействие электрически заряженных тел. Поле, созданное неподвижными электрическими зарядами, называется электростатическим.

Электростатическое поле в каждой точке характеризуется вектором напряженности Е и потенциалом φ. Напряженность поля Е  векторная физическая величина, численно равная силе, действующей на единичный пробный положительный заряд, помещенный в данную точку поля

. (3.1)

Потенциал поля φ  скалярная физическая величина, численно равная потенциальной энергии единичного пробного положительного заряда, помещенного в данную точку поля

. (3.2)

Напряженность и потенциал электростатического поля связаны между собой соотношением

, (3.3)

где dφ / dn  производная потенциала φ по нормали n к эквипотенциальной поверхности называется градиентом потенциала, который также обозначается gradφ

.

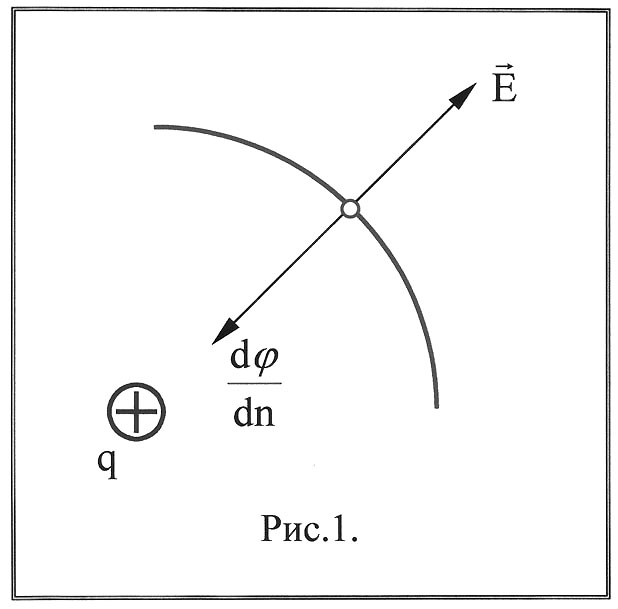
Рис. 3.1

Градиентом потенциала называется вектор, направление которого совпадает с направлением наибольшего увеличения потенциала, а величина равна изменению потенциала на единицу длины в направлении наибольшего изменения (рис. 3.1).

Графически электростатические поля изображаются с помощью силовых линий и эквипотенциальных поверхностей. Силовой линией электростатического поля или линией напряженности называется линия, касательная к которой в каждой точке совпадает с направлением вектора напряженности (сплошные линии на рис. 3.2).

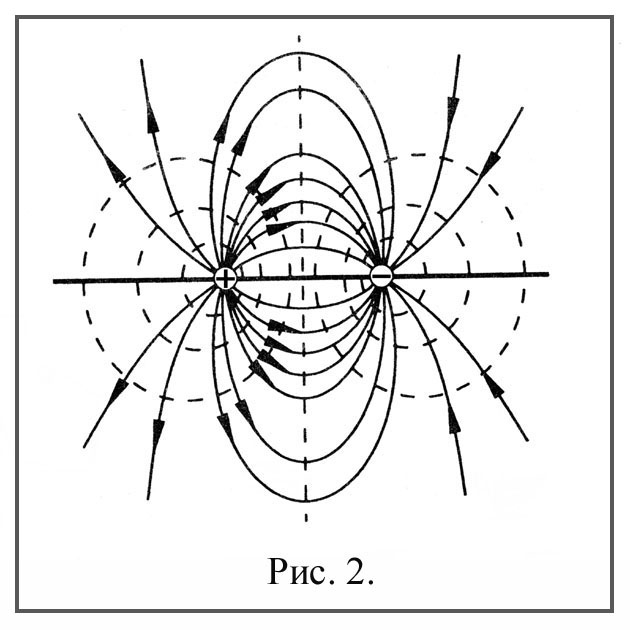
Рис. 3.2

Эквипотенциальная поверхность есть геометрическое место точек равного потенциала (пунктирные линии на рис. 3.2).

Силовые линии всегда перпендикулярны эквипотенциальным поверхностям. Действительно, работа dA сил электростатического поля по перемещению заряда q по эквипотенциальной поверхности на отрезке dl равна

,

так как изменение потенциала dφ = 0.

С другой стороны

где α  угол между направлением вектора Е и направлением отрезка dl.

Так как dA = 0, qEdlcosα = 0, E  0, dl  0, следовательно, cosα = 0, а α = 90^o.

Отсюда вытекает, что силовые линии электростатического поля перпендикулярны к эквипотенциальным поверхностям. Ортогональность силовых линий и эквипотенциальных поверхностей используется в данной работе для построения силовых линий электростатического поля по экспериментально установленному положению эквипотенциальных поверхностей.

Таким образом, силовые лини нормальны к поверхностям, находящимся в электростатическом поле проводников, являющихся телами с одним значением потенциала во всем объеме. Если найдены силовые лини, то по ним можно построить эквипотенциальные поверхности. И, наоборот, по найденным в эксперименте поверхностям можно построить силовые линии поля, т.е. можно найти значение вектора Е в каждой точке поля.

Экспериментальное измерение потенциалов оказывается значительно проще, чем измерение напряженности поля, т.к. большинство приборов измеряют именно разности потенциалов.

В основу изучения распределения потенциалов в электростатическом поле часто кладется так называемый метод зондов. Его сущность заключается в следующем: в исследуемую точку поля вводится специальный электрод – зонд, чтобы он своим присутствием минимально нарушал исследуемое поле. Это выполняется, если зонд имеет потенциал, равный потенциалу поля в данной точке в отсутствие зонда. Только тогда показания приборов, соединенных с зондом, будут давать правильную картину распределения потенциалов.

Но изучение электростатического поля является весьма трудной задачей, т.к. вынуждает применять высокочувствительные, точные и малонадежные приборы.

Поэтому был разработан особый метод изучения электростатического поля путем воспроизведения его структуры в проводящих средах, по которым пропускается ток. Оказывается, что при некоторых условиях распределение потенциалов в проводящей среде, по которым течет ток между установленными в ней электродами, может быть сделано тождественным с распределением потенциалов между теми же электродами, помещенными в непроводящую среду. Т.е. помещая электроды в проводящую среду, мы создаем потенциальную модель электростатического поля, а измерения распределения потенциалов в проводящей среде – сравнительно легкая задача.