Контрольные вопросы

1. Объясните полученные результаты.

2. Оцените погрешность измерений.

Литература: [3], [7], [11], [13], [16], [20], [21].

Лабораторная работа № 11 Изучение магнитного поля соленоида с помощью датчика Холла

Цель работы: познакомиться с холловским методом измерения индукции магнитного поля.

Сведения из теории

В пространстве, окружающем проводники с током или движущиеся заряды, возникает магнитное поле, которое можно обнаружить по воздействию его на другой проводник с током или магнитную стрелку. Магнитное поле в каждой точке пространства количественно может быть описано с помощью вектора напряжённости магнитного поля Н или с помощью вектора индукции магнитного поля В. В вакууме векторы В и Н связаны соотношением

(11.1)

где _о = 4·10^-7 Гн/м – магнитная постоянная.

Для вычисления напряжённости и индукции магнитного поля используют закон Био-Савара-Лапласа, согласно которому элементарная напряжённость магнитного поля dH, создаваемая элементом проводника с током Idl в некоторой точке пространства на расстоянии r, определяется выражением

(11.2)

Для нахождения результирующей напряжённости, создаваемой проводником конечных размеров, надо воспользоваться принципом суперпозиции магнитных полей и найти векторную сумму элементарных напряжённостей dH

(11.3)

В пределе сумма записывается в виде интеграла по контуру проводника с током. Применим формулу (11.3) для вычисления напряжённости магнитного поля на оси соленоида. Каждый виток соленоида – это круговой ток, поэтому первоначально вычислим напряжённость поля на оси кругового витка с током (рис. 11.1).

Рис. 11.1

При сложении составляющих магнитного поля dH_z, перпендикулярных оси ОА, они компенсируют друг друга вследствие симметрии контура. Поэтому результирующая напряжённость магнитного поля в точке А направлена вдоль оси кругового тока и равна по модулю

, (11.4)

(11.5)

В (11.5) учтено, что векторы dl и r взаимно перпендикулярны. Подставляя (11.5) в (11.4) и учитывая, что величины R и r постоянны, имеем

(11.6)

Перейдём теперь к вычислению поля соленоида, изображённого на рис. 11.2.

Рис. 11.2 Рис. 11.3

Пусть на единицу длины соленоида приходится n витков, тогда на участке dz будет ndz витков, которые в точке О согласно (11.6) создадут напряжённость

(11.7)

На рис. 11.3 отдельно изображены элемент dz, радиус-вектор r и углы Θ и dΘ.

Из геометрических построений рис. 11.2 и 11.3 следует

(11.8)

Подставляем (11.8) в (11.7) и интегрируем в пределах от Θ₁ до Θ₂.

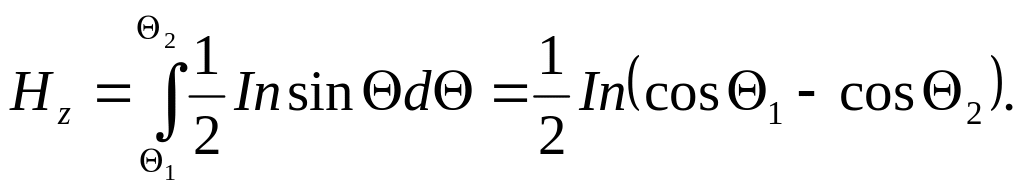(11.9)

В случае бесконечного соленоида

Θ₁ = 0, Θ_z = , H_z = In. (11.10)

Вопросы допуска

1. Сформулируйте закон Био-Савара-Лапласа. Пользуясь этим законом, дайте вывод формулы для индукции магнитного поля на оси кругового витка с током.

2. Сформулируйте теорему о циркуляции вектора В по контуру L. Пользуясь этой теоремой, дайте вывод формулы для индукции магнитного поля бесконечного соленоида.

3. Пользуясь принципом суперпозиции, дайте вывод формулы для индукции магнитного поля бесконечного соленоида.

4. Дайте вывод формулы для ЭДС Холла.

5. Нарисуйте схему измерений для исследования зависимости B = f (z).

6. Постройте зависимость B = f (I).