Практичне заняття №2

Тема 4. Проблеми процесу вироблення рішення

Тема заняття: Проблеми процесу вироблення рішення

Мета заняття: Закріплення теоретичних знань і формування практичних навичок щодо визначення окремих проблем процесу прийняття рішення.

Завдання:

3. Здійснити вибір оптимального групового рішення методом ранжування можливих альтернатив.

4. Здійснити вибір оптимального групового рішення методом матриці розбіжностей індивідуальних і групових рішень.

5. Здійснити вибір оптимального групового рішення методом середньої корисності для групи.

Методичні вказівки і приклад виконання практичного заняття.

Завдання 1. Здійснити вибір оптимального групового рішення методом ранжування можливих альтернатив.

Групі з трьох рівноправних компаньйонів необхідно прийняти загальне рішення, вибравши його з чотирьох можливих альтернативних варіантів. Кожний член групи по-різному оцінює можливі рішення. Ця оцінка наведена в табл. 2.1 на основі додання рішенням різних рангів (так зване ранжирування). Причому, чим нижче ранг, тим перевага більша.

Таблиця 2.1

Ранжирування можливих альтернатив

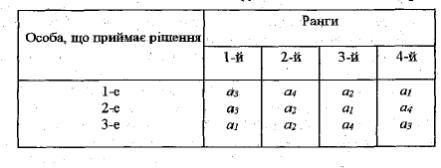
Необхідно знайти оптимальне групове рішення.

Ранги за кожною альтернативою складаються за такою формулою

Ранг альтернативи а_і = Σрангів альтернативи а_і всіх осіб, що приймають рішення

за альтернативою а₁ = 4 + 3 + 1 = 8

за альтернативою а₂ = 3 + 2 + 2 = 7

за альтернативою а₃ = 1 + 1 + 4 = 6

за альтернативою а₄ = 2 + 4 + 3 = 9

Групове рішення відповідає тій альтернативі, у якої сума рангів виявляється найменшою (Нагадаємо, що чим нижче ранг, тим більше переваг.)

В даному прикладі це альтернатива 3.

Завдання 2. Здійснити вибір оптимального групового рішення методом матриці розбіжностей індивідуальних і групових рішень.

Група з трьох рівноправних компаньйонів оцінює три альтернативних рішення за трьохбальиою системою: краще рішення — 3 бали, средне — 2, гірше — 1 бал (табл. 2.2)

Таблиця 2.2

Ранжирування альтернатив

Необхідно знайти таке групове рішення, при якому відхилення між вибором групи й індивідуальними рішеннями буде найменшим.

Для того, щоб мінімізувати наявні відхилення рішень членів групи від групового рішення, будується матриця розбіжностей результатів рішень (табл. 2.3). При цьому спочатку робляться передбачення про вибір групою тої чи іншої альтернативи, а потім оцінюються розбіжності між цим груповим й індивідуальними рішеннями. Так, якщо групове рішення відповідає альтернативі а₁, (оцінка 3 бали), то розбіжності між думкою колективу й індивідуальним вибором 1-го особи дорівнює нулю, якщо ж група зупинилася на варіанті а2 (1 бали), то розбіжності між нею і 1-ою особою складе 2 бали, і т.д.

Таблиця 2.3

Матриця розбіжностей індивідуальних і групових рішень

Групові рішення	Індивідуальні рішення			Максимальні розбіжності
	1-а особа	2-а особа	3-я особа
а1	1	0	2		2
а2	2	2	0		2
а3	0	1	1		1
Найменше відхилення				1

Далі в рядках для кожної альтернативи знаходяться максимальні розбіжності, а потім з цих максимальних розбіжностей — найменше, в даному випадку 1 бал. Цій розбіжності відповідає альтернатива а3, яка й визнається кращим рішенням.

При такій стратегії вибору можна стверджувати, що у випадку прийняття групою рішення а3 для будь-якої особи розбіжності його рішення з рішенням групи залишається мінімальним і що не перевищує 1 бала.

Завдання 3. Здійснити вибір оптимального групового рішення методом середньої корисності для групи.

Припустимо; рішення приймається групою з двх осіб. Можливі два альтернативних варіанти рішення: а₁ і а₂. Оцінки корисності цих варіантів обома особами для двох можливих результатів показані в табл. 2.4 і 2.5. Ймовірності результатів для кожної особи, звичайно, різні.

Таблиця 2. 4

Матриця корисності для 1-ої особи

Таблиця 2.5

Матриця корисності для 2-ої особи

Поскільки 1-а особа оцінює вище користь першого варіанта, а 2-а особа — другого, при прийнятті групового рішення прийти до спільної думки неможливо. В цьому випадку теорія рішень, як правило, пропонує грунтуватися на середніх величинах: середніх ймовірностях результатів і середніх корисностях (табл. 2.6).

Таблиця 2.6

Матриця середньої корисності для групи

Варіанти рішення	Середні ймовірності результатів			Корисність за двома результатами
	0,3	0,7
а1	-5	+8	-5*0,3+8*0,7=+4,1
а2	+30	-5	+30*0,3-5*0,7=+5,5

Тепер видно, що група повинна вибрати варіант а2.