
- •Предмет и основные задачи математической статистики
- •Первичная обработка данных наблюдений. Построение закона распределения по статистическим данным Основные определения.
- •Первичная обработка опытных данных.
- •Можно нанести данные из статистического ряда распределения на график. Это принято делать одним из двух способов:
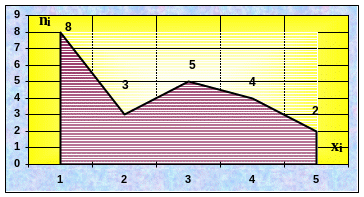
- •Левый график называется полигоном частот (статистический аналог многоугольника распределения). Правый чаще используется в западной литературе (аналог теоретической функции вероятности).
- •Первичная обработка данных наблюдений. Построение закона распределения по статистическим данным Основные определения.
- •Первичная обработка опытных данных.
- •Числовые характеристики выборки
Можно нанести данные из статистического ряда распределения на график. Это принято делать одним из двух способов:
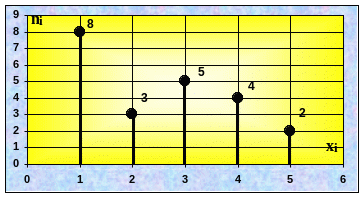



Левый график называется полигоном частот (статистический аналог многоугольника распределения). Правый чаще используется в западной литературе (аналог теоретической функции вероятности).
Пример:
получена выборка 1,3,5,2,1,4,1,5,5,4,2,3,3,3,1.
объем ее равен 15: n = 15.
Вариационный ряд 1,1,1,1,2,2,3,3,3,3,4,4,5,5,5
Группируем данные по повторяемости, подсчитываем частоты n i заносим в таблицу
х i |
1 |
2 |
3 |
4 |
5 |
n i |
4 |
2 |
4 |
2 |
3 |
С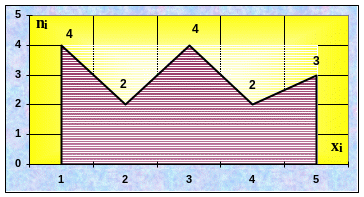 умма
всех частот должна быть равна
умма
всех частот должна быть равна
Нанося данные на график, получаем полигон частот:
Подсчитываем относительные частоты w i , заносим в таблицу, получаем статистический ряд распределения:
х i |
1 |
2 |
3 |
4 |
5 |
w i |
4/15 |
2/15 |
4/15 |
2/15 |
3/15 |
Сумма всех относительных частот должна быть равна 1 (основное свойство ряда распределения, проверьте)
П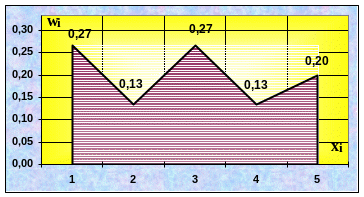 олигон
относительных частот
выглядит точно так же, как и полигон
частот, меняется только масштаб на оси
ординат.
олигон
относительных частот
выглядит точно так же, как и полигон
частот, меняется только масштаб на оси
ординат.
Для непрерывной случайной величины Х опытные данные практически повторятся не будут, т.к. возможных значений бесконечно много. Записывается вариационный ряд.
х 1 ≤ х 2 ≤ х 3 ≤ . . . . ≤ х n
Затем выполняется интервальная группировка данных:
Длина промежутка от x min до x max называется размахом варьирования
![]() .
.
Разбиваем этот промежуток на одинаковые элементарные интервалы.

Их
количество зависит от объема выборки
и подсчитывается по формуле Стерджеса:
![]() .
.
Полученное число нужно округлить до ближайшего целого (число интервалов дробным быть не может). После этого длину каждого элементарного интервала находим по формуле:
![]() .
.
При расчетах вручную, без компьютера, x можно округлять и начало первого интервала тоже брать приближенное. Границы остальных интервалов получим, добавляя шаг за шагом x :
x 1 = x о+x; x 2 = x 1+x; x 3 = x 2+x и т.д.
Записываем в таблицу эти элементарные интервалы и для каждого из них частоту n i попадания в него ( количество опытных данных, попавших в каждый интервал). Сюда же заносим относительные частоты : w i = n i / n = n i / n.
(x i ;x i+1) |
(x 0 ;x 1) |
(x 1 ;x 2) |
(x 2 ;x 3) |
|
(x k-1 ;x k) |
n i |
n 1 |
n 2 |
n 3 |
|
n k |
w i |
w 1 |
w 2 |
w 3 |
|
w k |
Это – интервальный ряд распределения.
Для непрерывной случайной величины закон распределения задается в виде плотности распределения f(x). Вероятность попадания случайной величины в любой интервал (a, b) - это площадь под графиком плотности, опирающаяся на интервал (a, b) .
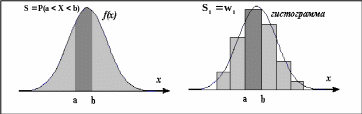
Когда по данным наблюдений найдены относительные частоты w i попадания в разные интервалы, можно и построить прямоугольники соответствующей площади. Тогда полученная фигура (гистограмма) покажет нам , какой должна быть плотность распределения .
Гистограмма относительных частот:
на каждом элементарном интервале строим прямоугольник, по площади равный относительной частоте попадания в интервал.
Высоты этих прямоугольников равны:
![]() .
.
Замечание: гистограмма относительных частот дает приближенную информацию о плотности распределения. Все предположения о виде закона распределения предстоит проверять с помощью специальных процедур (см. статистическая проверка гипотез).
Чем больше опытов проводится, тем ближе построенная гистограмма к теоретической плотности распределения.
Итак, мы уже выяснили, как по данным наблюдений получить представление о ряде распределения и о плотности распределения. Осталось разобраться с функцией распределения.
Для любой случайной величины универсальным способом задания закона распределения является функция распределения F(x). По определению, функция распределения - это вероятность попадания случайной величины в область, лежащую слева от аргумента x : F(x) = P(X<x).
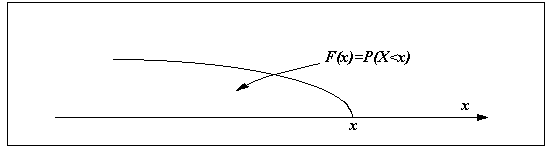
Из эксперимента мы можем найти относительную частоту попадания в область, лежащую слева от аргумента, и это будет эмпирическая или статистическая функция распределения :
О2 : Статистическая (эмпирическая) функция – это функция, которая для каждого значения аргумента равна относительной частоте попадания опытных данных в область, лежащую слева от аргумента.
F*(x) = W(X<x).
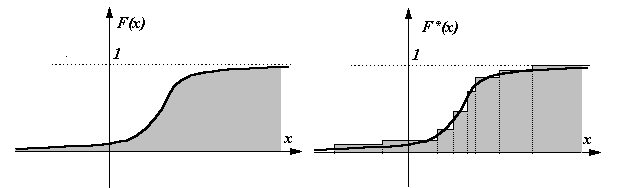
Если построить график статистической функции распределения F*(x), то это будет изображенная справа ступенчатая фигура, которая позволяет получить представление о характере теоретической функции распределения F(x).
Технология построения статистической функции распределения F*(x) такая же, как и для теоретической функции распределения для дискретных случайных величин: суммируются относительные частоты для всех опытных значений, лежащих слева от аргумента (как раньше суммировались вероятности).
![]()
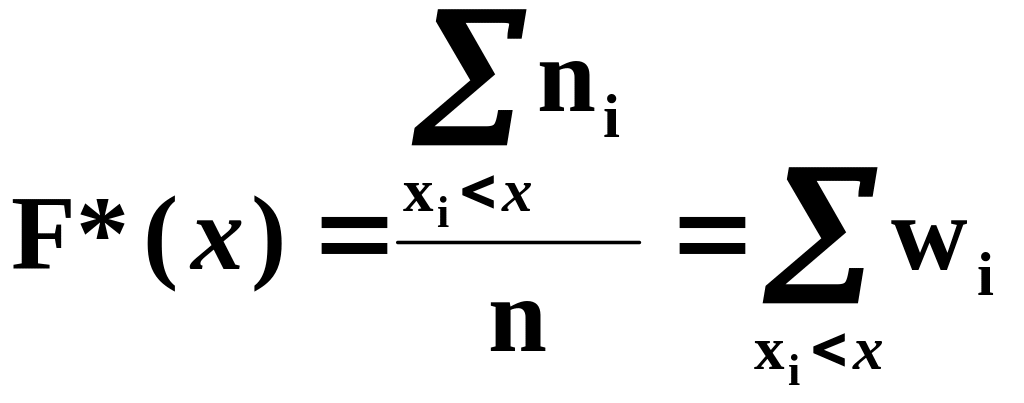
Замечание: Так как с увеличением числа опытов относительные частоты приближаются к вероятностям, делаем вывод, что с увеличением количества наблюдений ступенчатая статистическая функция распределения приближается к теоретической функции распределения.
Пример:
задана выборка 2,7,2,5,9,5,2,7,5,5.
построить статистическую функцию распределения.
объем выборки равен 10 : n = 10.
Вариационный ряд 2,2,2,5,5,5,5,7,7,9.
Группируем данные по повторяемости, подсчитываем частоты n i заносим в таблицу
х i |
2 |
5 |
7 |
9 |
n i |
3 |
4 |
2 |
1 |
Подсчитываем относительные частоты w i , заносим в таблицу, получаем статистический ряд распределения:
получаем
|
2 |
5 |
7 |
9 |
w i |
0.3 |
0.4 |
0.2 |
0.1 |
Для наглядности изобразим данные наблюдений на числовой оси.
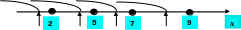
Возьмем любое значение x, меньшее 2. Слева от такого x не наблюдалось ни одного опытного значения. Частота и относительная частота попадания в эту область равна нулю. При x = 2 она тоже равна нулю:
x 2: F*(x) = 0.
Для любого 2 < x 5: слева от такого x 3 раза наблюдалось значение 2, т.е., относительная частота попадания в эту область равна 0,3.
2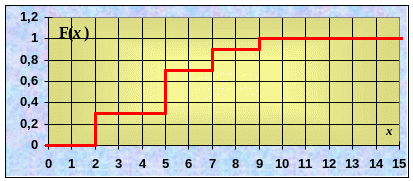 < x
5: F*(x)
= 0,3.
< x
5: F*(x)
= 0,3.
Дальше аналогично:
5 < x 7: F*(x) = 0,7.
7 < x 9: F*(x) = 0,9.
9 < x < : F*(x) = 1,0.
Таким образом, получаем следующий график:
Е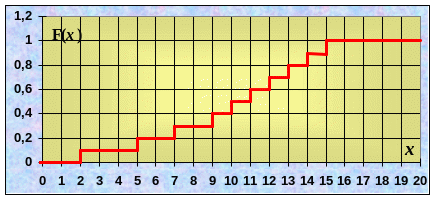 сли
опытные данные не повторяются (непрерывная
случайная величина), то частота каждого
из них равна 1, а относительная частота
w
i=1/n.
При построении F*(x)
при переходе через очередное опытное
значение F*(x)
увеличивается на 1/n.
сли
опытные данные не повторяются (непрерывная
случайная величина), то частота каждого
из них равна 1, а относительная частота
w
i=1/n.
При построении F*(x)
при переходе через очередное опытное
значение F*(x)
увеличивается на 1/n.
Замечание: Если объем выборки n возрастает, то относительная частота w i приближается к вероятности p i и статистическая функция распределения F*(x) приближается к теоретической функции распределения F (x).
