5. Проверка коэффициентов канонических уравнений

Каждый коэффициент можно проверить кинематическим способом по формулам:

где M_p⁰- эпюра моментов от нагрузки в статически определимой системе, полученной из заданной системы путем удаления всех лишних связей. Знак «×» обозначает интеграл Мора [1], который вычисляется по формуле Симпсона (5) или Верещагина (6). Найденный коэффициент сравнивается со значением, полученным статическим способом.

где m – количество участков на эпюре, L – длина участка, “л”,“с”,“п” – соответственно левое, среднее, правое значения на участке эпюры. Знак произведения положительный, если оба значения лежат по одну сторону от оси балки. Ω - площадь первой эпюры, У_с – ордината на второй эпюре, взятая под центром тяжести первой эпюры. Если одна эпюра криволинейная, то берется ее площадь.

Например, в задаче 5 коэффициент r₁₁ можно получить перемножением единичной эпюры (рис. 3,а) на себя , а коэффициент R_1p - перемножением эпюры M_p⁰ на ₁. На рис. 3,б,в приведена статически определимая система под действием заданных нагрузок и ее эпюра моментов M_p⁰.

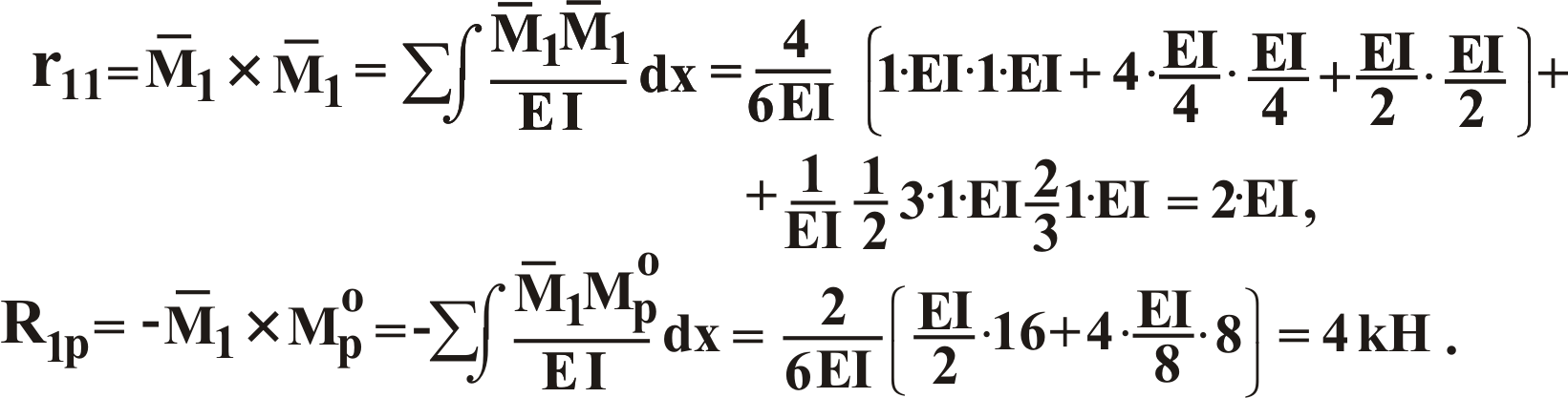
Рис.3

Для задач один раз кинематически неопределимых в канонических уравнениях коэффициентов всего два, и целесообразность их проверки невелика, поэтому раздел 5 в примерах на рис. 5 и 6 отсутствует.

Для n ≥ 2 перед решением канонических уравнений целесообразно проверить правильность вычислений коэффициентов. На основании теоремы Релея о взаимности реакций [1] в канонических уравнениях коэффициенты, симметрично расположенные относительно главной диагонали, должны быть равны, то есть = . Например, при n = 2 по теореме Релея равны между собой два коэффициента (7). Не целесообразно проверять каждый коэффициент по отдельности, поскольку должна выполняться универсальная проверка коэффициентов r_ij (8) и проверка грузовых коэффициентов (9)

где M_s - суммарная эпюра получается путем сложения ординат единичных эпюр. Проверки (8), (9) выполнены в примере на рис. 7.

6. Решение системы канонических уравнений

Для систем один раз кинематически неопределимых (n=1) каноническое уравнение (2) одно и решение имеет вид

Для систем два раза кинематически неопределимых решение системы уравнений (3) и (4) имеет вид:

7. Построение окончательной эпюры изгибающих моментов Мок.

Окончательная эпюра М_ок в соответствии с принципом независимости действия сил получается путем сложения «исправленных» эпюр ∙Z_i с грузовой:

«Исправленные» эпюры ∙Z_i получаются путем увеличения всех ординат единичных эпюр в Z_i раз. Если Z_i < 0, то измененные ординаты откладываются с другой стороны от оси стержня.

Каждое значение на эпюре М_ок получается по формуле (10). Например, на рис. 7,п значение момента в узле 4 равно сумме момента М_4,р в узле 4 грузового состояния рис 7,ж и моментов М_4,1, М_4,2 в узле 4 в первом и втором единичных состояниях рис. 7.н и 7.о. Значения слева от оси балки приняты положительными

М_4,ок = М_4,р + М_4,1 + М_4,2 = 2 + 5.417 – 0.9445 = 6.4725 кН∙м.