4.3. Особенности напряженного состояния материала при свободном прямоугольном резании

Рассмотрим вопрос применительно к сливной стружке. На срезаемый слой действуют нормальная сила 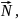которая создает силу трения В сумме эти силы дают т. н. силу стружкообразования

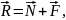
наклонную к поверхности резания под углом действия

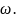
Разложим силу

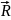
на силу

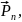
перпендикулярную к плоскости

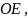
и силу

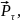
действующую вдоль этой плоскости.

Под действием сил

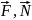
на поверхности стружки, контактирующей с передней поверхностью инструмента, возникают, соответственно, напряжения

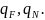
Под действием сил

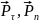
на плоскости возникают, соответственно, реактивные напряжения

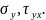
Выделим элементарный куб, одна из граней которого лежит в плоскости а другая параллельна плоскости схемы.

Эксперименты показывают, что напряжение

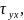
действующее по линии

изменяются незначительно, поэтому его считают постоянным. В соответствии с уравнениями теории упругости из этого допущения следует, что

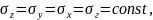
где 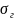‑ это т. н. гидростатическое давление.

Получается, что элементарный куб находится в условиях всестороннего равномерного сжатия, когда напряжение не влияет на значения касательных напряжений, и его можно не учитывать. В итоге приходим к тому, что напряженное состояние в срезаемом слое является простым сдвигом, причем, в соответствии с законом парности касательных напряжений, напряжения

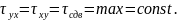
Для определения положения главной площадки с максимальным напряжением необходимо площадку с большим (в алгебраическом смысле) нормальным напряжением повернуть на требуемый угол (в данном случае 45°) в направлении, в котором вектор касательного напряжения, действующего по этой же площадке, стремится вращать элементарный параллелепипед относительно его центра. При этом

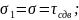
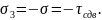
Напряжение сдвига можно определить следующим образом:

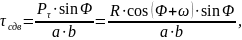
где

‑ это ширина срезаемого слоя.

Основные допущения, при которых справедлива полученная формула:

1) напряженно-деформированное состояние в зоне резания – плоское;

2) деформации в зоне резания локализуются вблизи одной плоскости;

3) напряжение сдвига постоянно.

Несмотря на сделанные допущения, полученная формула хорошо согласуется с опытными данными. Однако, в общем случае, напряжение сдвига непостоянно и вывод, полученный с учетом указанных допущений касательно постоянства напряжения , в основном не подтверждается на практике.

4.4. Особенности пластической деформации материала при свободном прямоугольном резании

Рассмотрим вопрос применительно к сливной стружке. Предположим, что вершина режущего клина должна переместиться из положения

в положение

на расстояние

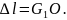
При этом точка

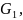
срезаемого слоя в виде параллелограмма

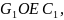
лежащая на поверхности резания, окажется в точке

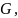
лежащей на передней поверхности инструмента, а точка

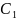
окажется в точке

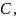
лежащей на свободной стороне стружки. Таким образом, параллелограмм

сдвигаясь вдоль основания

на

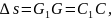
превращается в параллелограмм

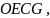
который принадлежит не срезаемому слою толщиной

а стружке толщиной

Плоскость

называют плоскостью сдвига, а угол

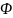
‑ углом сдвига. Сдвиговая деформация начнется в том случае, когда напряжение сдвига станет равным или большим, чем предел текучести на сдвиг:

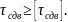
При дальнейшем перемещении инструмента указанный процесс повторится в результате непрерывных сдвигов тонких слоев материала по плоскости сдвига без нарушения связи между сдвинутыми слоями, т. е. без нарушения сплошности материала стружки.

Расстояние

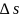
является абсолютным сдвигом. В теории пластических деформаций для характеристики интенсивности сдвига пользуются величиной

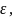
называемой относительным сдвигом. Он равен отношению абсолютного сдвига к толщине слоя

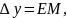
претерпевшего этот сдвиг, т. е.

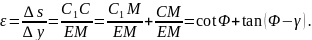
Для определения относительного сдвига при определенном угле

необходимо знать угол сдвига. Его можно определить по длине стружки. Пусть при перемещении инструмента на расстояние

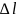
длина стружки составила

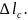
Отношение

получило название коэффициента усадки или укорочения стружки. Данную формулу называют формулой Тиме. С ее помощью можно выразить угол сдвига через коэффициент усадки стружки:

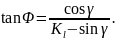
Определим, при каком

относительный сдвиг будет минимальным. Для этого возьмем первую производную уравнения, приравняем ее к нулю и решим уравнение относительно угла сдвига:

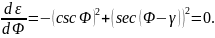
Это условие справедливо при

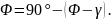
Тогда

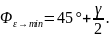
Зная относительный сдвиг, можно определить скорость деформации, которая представляет собой относительную деформацию в единицу времени деформации, т. е.

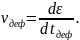
От скорости деформации зависит температура, сопровождающая процесс деформации: чем выше скорость деформации, тем меньше требуется для этого энергии и меньше тепловыделение.

Пластические деформации материала срезаемого слоя при резании ограничиваются зоной стружкообразования. Наиболее интенсивно пластическая деформация протекает в очень узкой зоне, которую для упрощения расчетов принимают за прямоугольник толщиной

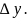
Время равномерной деформации обрабатываемого материала на этом участке составит

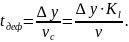
При этом

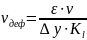
Скорость деформации при резании очень высока. При обработке конструкционных материалов обычного качества

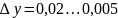см; ; .

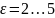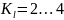При скорости резания 60 м/мин скорость деформации приблизительно равна 4000 c^-1.

Высокие скорости деформации не позволяют установить четкую границу между хрупкими и пластичными материалами, поскольку один и тот же материал в зависимости от характера напряженного состояния при резании и скорости деформации может вести себя и как хрупкий, и как пластичный. Так, например, при точении чугуна стружка может быть сливной, при обработке вязких сталей ‑ элементной.

В результате пластической деформации в стружке образуется текстура в виде полос или строчек, расположенных под некоторым углом к плоскости сдвига, называемым углом текстуры

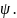
Линии текстуры представляют цепочки деформированных зерен стружки, получивших после прохождения через плоскость сдвига определенную форму и ориентацию.

Значение угла текстуры можно определить из выражения:

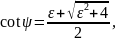
где