3. Связь между параметрами интерференционной системы и схн

Параметрами интерференционной системы, определяющими ее структуру и свойства при заданном распределении чувствительности ее элементов, являются:

• число элементов (сейсмоприемников) n;

• база x=(n-1)x (теоретическая база x_Т);

• шаг элементов .

Параметрами характеристики направленности, определяющими направленное действие ИС, являются:

• ширина полосы пропускания 0 æ^ æ^_ГР

• ширина полосы подавления æ^₀₁æ^ æ^_ОП

• степень подавления (помехоустойчивость) ( при h(x)=1).

В соответствии с основным свойством интерференционных систем, связь между параметрами ИС и параметрами ее СХН может быть установлена на основании спектральных теорем о Фурье - трансформантах. Так, теорема масштабов определяет обратную пропорциональность базы ИС и ширины главного максимума СХН (ширины полосы пропускания). Теорема дискретизации объясняет обратную пропорциональность шага элементов ИС и периода ее СХН (ширины полосы подавления).

Анализ влияния параметров ИС на параметры ее СХН несколько осложняет взаимозависимость параметров ИС. Всегда изменение какого-либо одного параметра ИС ведет к изменению второго.

В таблице 1.1 условными знаками изображено влияние параметров интерференционной системы с равномерной чувствительностью элементов на параметры ее спектральной характеристики направленности. Знак «+» соответствует увеличению параметра, знак «-» - уменьшению, знак «=» - его неизменности.

Таблица 1.1

Влияние параметров интерференционной системы на параметры спектральной характеристики направленности

Параметры ИС				Параметры СХН
Число элементов n	Шаг элементов	Теоретическая база xT = nx	Помехо-устой-чивость	Полоса подавления		Полоса пропускания æГР = æ01
				æ01 =	æОП =
+	=	+	+	-	+	-
+	-	=	+	=	+	=
=	+	+	=	-	-	-

Как можно заключить из анализа таблицы, увеличение числа элементов однозначно увеличивает помехоустойчивость. Изменение шага элементов всегда ведет к обратному изменению ширины полосы подавления. Увеличение базы всегда сужает ширину полосы пропускания.

4. Виды характеристик направленности

Многообразие представлений аргумента СХН (4) дает возможность получить различные виды характеристик направленности.

Частотной характеристикой направленности (ЧХН) называется СХН, представ-ленная в виде функции частоты (рис.1) при параметре V^ (или - запаздывание волны между соседними элементами ИС). ЧХН описывает искажения интерференционной системой спектра волны, пришедшей к базе ИС по заданному направлению. Аргументом ЧХН является частота f, которая пересчитывается из æ^= , то ЧХН равна: ( f)= (10)

Значения аргумента, соответствующие характерным точкам ЧХН, сведены в таблице 1.2.

Таблица 1.2

Связь различных аргументов СХН

Виды СХН	Аргумент	Границы полосы подавления		Период
		Первый нуль	Последний нуль
1	2	3	4	5
Волновая Н(æ)	æ =	æ01 =	æОП =
Частотная H(f)	f = æ			;
Обобщенная H(y)	y = 2xæ			2

Для расчета характеристик направленности удобно использовать обобщенные спектральные характеристики направленности (рис.2) как функции аргумента у, равного

2xæ^ (11)

и называемого обобщенным аргументом.

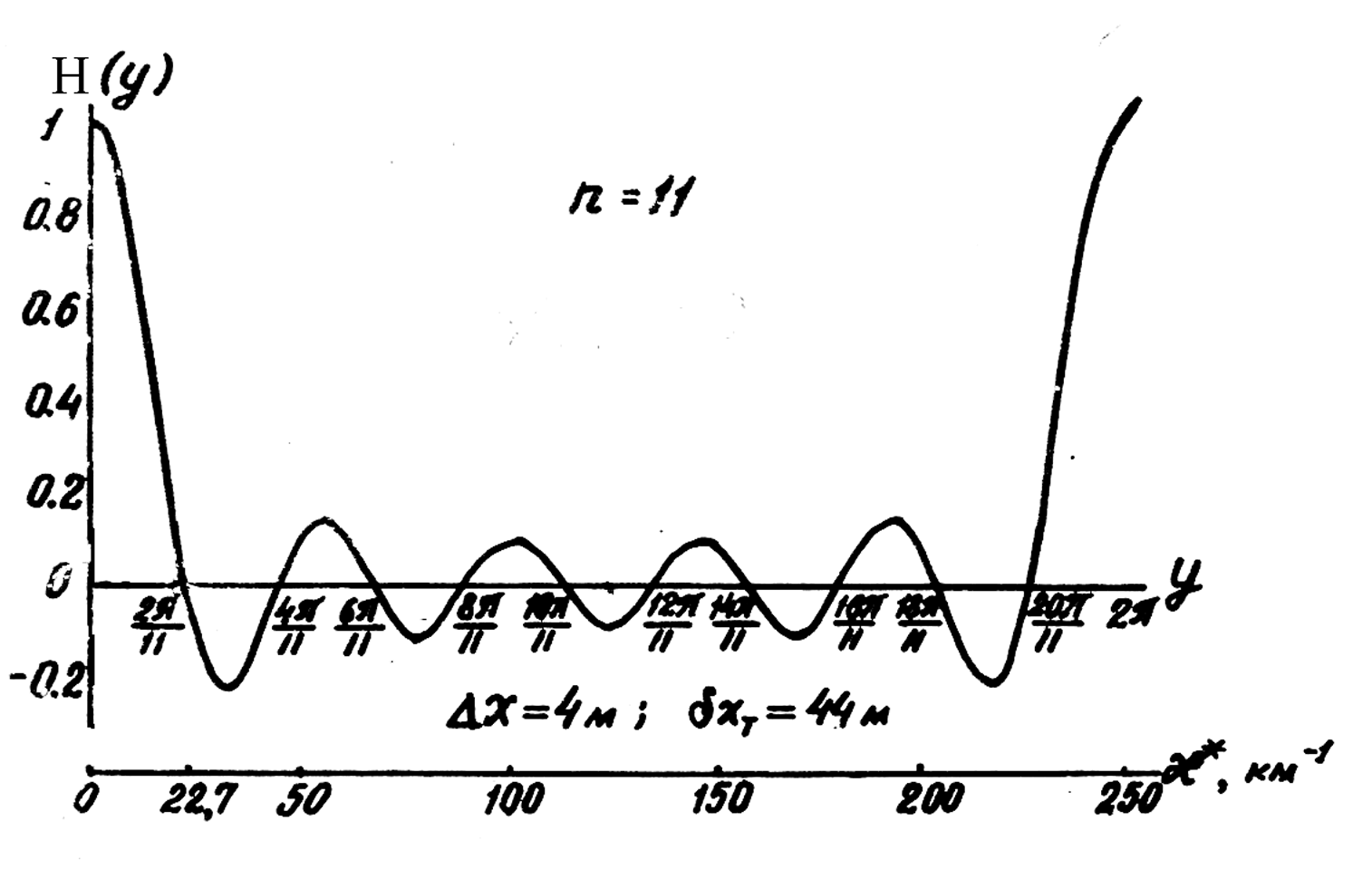
Рис 2. Обобщенная характеристика направленности

Обобщенная нормированная СХН ИС с равномерной чувствительностью элементов рассчитывается по формуле:

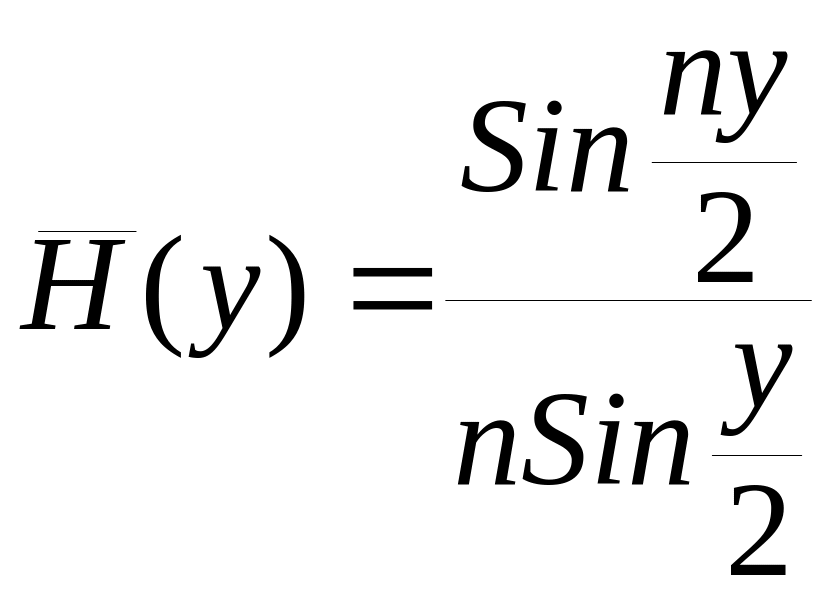(12)

Значения обобщенного аргумента, соответствующие характерным точкам СХН, приведены в таблице 1.2.

Примечание. Граница полосы пропускания æ^_ГР не имеет явного аналитического выражения через параметры ИС и определяется по графику соответствующей нормированной СХН из условия = . Так как (0,5 æ^₀₁) меняется от 0,707 до 0,637, то для приближенных оценок можно считать, что граница полосы пропускания находится посередине между нулевым значением аргумента и его значением, соответствующим первому нулю:

æ^_ГР  0,5 æ^₀₁ (13)

В таблице 1.3 сведены вместе формулы связи различных аргументов упомянутых СХН.

Таблица 1.3

Связь аргументов различных видов СХН

æ
f	æV		æ
y	2xæ