Метод простой итерации

Пусть задано уравнение (6.1), где f(x) – непрерывна и найден интервал [a, b], содержащий только один корень.

Уравнение (6.1) представим в виде

x =  (x) (6.13)

Выбираем начальное приближение x = c₀ и, подставив в (6.13), находим следующее приближение c₁ =  (c₀) и т.д.

По аналогии

с_n+1 =  (c_n), n = 0, 1, 2, … (6.14)

Геометрическая интерпретация метода:

С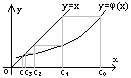 троим графики функций y = x и y =  (x) (левая и правая части уравнения (6.13)).

Каждый действительный корень с является абсциссой точки пересечения кривой y =  (x) и прямой y = x .

Оценка погрешности n – го приближения

, (6.15)

где .

Тема 7 Решение систем нелинейных уравнений (сну)

Рассмотрим систему нелинейных уравнений

(7.1)

………

В отличие от систем линейных уравнений для систем нелинейных уравнений не существует прямых методов решения, поэтому всегда применяются итерационные методы.

Метод простой итерации

Метод простой итерации для СНУ является развитием аналогичного метода для решения одного уравнения. Он основан на допущении, что систему (7.1) можно привести к виду

(7.2)

………

Эта разновидность метода простой итерации построена аналогично методу Зейделя для СЛУ, когда для нахождения каждого последующего значения неизвестных используются вновь найденные значения предыдущих приближений.

.

(7.3)

………

Итерационный процесс заканчивается, когда изменения всех неизвестных в двух последовательных итерациях не станут меньше заданного малого числа

, i = 1, 2, …, n (7.4)

Недостаток метода:

При неудачном выборе начальных приближений неизвестных процесс может расходиться.

С увеличением числа неизвестных область сходимости уменьшается, и, в случае больших систем, сходимость обеспечивается лишь в том случае, если исходные значения очень близки к решению.

Метод Ньютона

Совокупность аргументов x₁, x₂, …, x_n системы (7.1) можно рассматривать как n - мерный вектор, а совокупность функций f₁, f₂, …, f_n как n - мерный вектор – функцию.

, .

Уравнение (7.1) можно записать в матричном виде

(7.5)

Приближенно заменим систему (7.5) линейной алгебраической системой.

Для этого разложим в ряд Тейлора по степеням , где , и опустим в разложении члены второго и более высоких порядков.

(7.6)

Определителем полученной системы линейных уравнений (7.6) относительно является определитель матрицы Якоби (якобиан), подсчитанный для

^(7.7)

Для существования единственного решения системы (7.1) якобиан системы (7.7) должен быть отличен от 0 на каждой итерации.

^Если , ^{то (7.6) можно переписать}

и т.д. (7.8)

Таким образом,

, k = 0, 1, 2, … (7.9)

Итерационный процесс заканчивается, когда изменения всех неизвестных в двух последовательных итерациях не станут меньше заданного малого числа

, i = 1, 2, …, n ...

Существенная трудность, возникающая при использовании метода Ньютона, заключается в необходимости вычисления якобиана (7.7) для каждой итерации.

Если непрерывна в окрестности искомого решения, и начальное приближение достаточно близко к нему, то можно условно принять

. (7.10)

Принятое допущение используется при построении расчетной формулы модифицированного метода Ньютона

, k = 0, 1, 2, … (7.11)