Общие замечания по отделению корней

Для выделения интервалов, в которых находятся действительные корни уравнения (6.1), если f(x) – непрерывная функция, можно воспользоваться следующими предположениями:

- если на концах некоторого отрезка непрерывная функция принимает значения разных знаков, то на этом отрезке уравнение (6.1) имеет хотя бы один корень

f(а)∙ f(b) < 0; (6.2)

• если при этом функция имеет 1 - ю производную, не меняющую знака, то корень единственный

f ‘(а)∙ f ‘(b) > 0. (6.3)

Д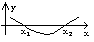 ля отыскания начальных приближений иногда удобно применять графический метод:

а) построить график функции y = f(x) и найти абсциссы точек пересечения графика с осью х;

б) если функция f(x) сложная, представить уравнение (6.1) в виде φ(x) = ψ(x) и построить графики функций y = φ(x) и y = ψ(x), найти абсциссы точек пересечения этих графиков.

П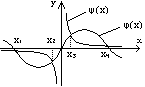 ример:

x ∙ sin x =1 , или sin x =1/ x

φ(x) = sin x; ψ(x) =1/ x

Метод половинного деления

Пусть задано уравнение (6.1), где f(x) – непрерывна и найден интервал [a, b], содержащий только один корень, т.е. f(а)∙ f(b) < 0.

Для определенности будем считать f(а) < 0, f(b) > 0.

Н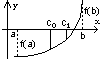 айдем значение f(c₀), где - начальное приближение. Последующие приближения будем определять по формуле , а = с₀, если f(c₀)∙ f(b) < 0,

или по формуле , b= с₀ , если f(a)∙ f(c₀) < 0 и т.д.

Условие прекращения итерационного процесса .

Метод имеет малую скорость сходимости.

Погрешность оценивается выражением

(6.4)

Метод хорд (секущих, ложного положения)

Пусть задано уравнение (6.1), где f(x) – непрерывна и найден интервал [a, b], содержащий один корень, т.е. f(а)∙ f(b) < 0.

В основе метода лежит линейная интерполяция по 2 значениям функции, имеющим разные знаки.

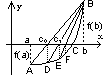Уравнение хорды АВ

(6.5)

В качестве приближений к корню принимаются значения с₀, с₁,..., с – точек пересечения хорд с осью абсцисс.

Для точки пересечения с осью х хорды АВ (х = с₀, y = 0) получим уравнение

Если f(c₀)∙ f(b) < 0, корень на интервале [c₀,b],

Следующая итерация: точка c₁ пересечения с осью х хорды BD (х = с₁, y = 0), а = с₀ и т.д.

(6.6)

Условие прекращения итерационного процесса

Оценка погрешности n – го приближения

(6.7)

где , . (6.8)

Метод Ньютона (касательных)

Пусть задано уравнение (6.1), где f(x) – непрерывна и найден интервал [a, b], содержащий только один корень, с₀ – начальное приближение.

В отличие от первых двух методов, для определения интервала, в котором заключен корень, не требуется определять значение функции с противоположными знаками.

Вместо интерполяции осуществляется экстраполяция с помощью касательной к кривой в данной точке (ее пересечение с осью абсцисс).

В основе лежит разложение в ряд Тейлора

^или

Д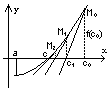 ано f(x) = 0, x  [a, b],

c₀ – начальное приближение

Уравнение касательной в т. М₀ (c₀, f(c₀))

Первое приближение c₁ – абсцисса точка пересечения касательной к точке М₀ с осью х (c₁, 0).

Из выражения

получим и т.д.

, n = 0, 1, 2,… (6.9)

Замечание: начальное приближение c₀ целесообразно выбирать так, чтобы

(6.10)

Теорема (достаточное условие сходимости):

Пусть f(x) определена и дважды дифференцируема на [a, b], причем f(a) f(b)<0, а и сохраняют знак на [a, b]. Тогда, исходя из начального приближения , удовлетворяющего (6.10), последовательность (6.9) сходится к единственному на [a, b] решению x = c уравнения (6.1).

Трудности метода Ньютона состоят в определении:

1. начального приближения x = c₀, которое должно находиться вблизи корня уравнения;

2. первой производной , отличной от 0, что не требуется в первых двух методах.

Объем вычислений метода Ньютона больше, но скорость сходимости выше.

Этот метод не рекомендуется при почти горизонтальных графиках кривых.

Оценка погрешности n – го приближения

(6.11)

где .

При этом быстрая сходимость обеспечена, если начальное приближение c₀ удовлетворяет неравенству

(6.12)