Тема 5 Итерационные методы решения слау

Итерационные методы особенно эффективны при большом порядке СЛАУ.

Предварительно приведем систему (4.1) к виду

, где ,

, (5.1)

........................

,

Исходя из начального приближения , получают векторы ,..., по рекурентной формуле

. (5.2)

Здесь F_k – некоторая функция, зависящая от матрицы коэффициен-тов А системы (4.2), правой части , номера приближения k и предыдущих приближений .

Метод имеет 1-й порядок, если F_k не зависит от , а зависит только от .

Метод стационарный, если F_k не зависит от k.

Простейший случай: если F_k - линейная функция, то общий линейный метод 1 – го порядка должен иметь вид

(5.3)

Здесь А – квадратная матрица, - вектор.

Метод Якоби (простой итерации)

К виду (5.3) можно привести, например, выделением диагональных элементов (для i – строки)

, ^{i = 1, 2, ..., n (5.4)}

Строим последовательность векторов, начиная с произвольного вектора ( , i = 1, 2, ..., n)

, , ... , ,

где , i = 1, 2, ..., n (5.5)

Метод Гаусса - Зейделя

В этом методе уточненное значение x₁ сразу же используется для вычисления x₂, а x₁ и x₂ для вычисления x₃ и т.д.

Зададимся начальным приближением неизвестных.

Обычно принимают , , ... , .

Начальные приближения подставляют в 1-е уравнение системы (5.1).

,

затем подставляем , , ... , во 2-е уравнение

.

Подставляем , , , ... ,

Подставляем , , ... , , выполним 2-ю итерацию.

Приближения с номером k определим по формуле

(5.6)

...................

,

Т.е. координаты вектора определяют по формуле

, i = 1, 2, ..., n (5.7)

Для сходимости метода необходимо, чтобы

1. все диагональные элементы были отличны от 0 (a_ii ≠ 0);

2. диагональные элементы значительно преобладали над остальными коэффициентами матрицы А.

В общем случае критерий окончания итерационного процесса при заданной допустимой погрешности ε > 0 определяется:

• по абсолютным отклонениям в виде

, i = 1, 2, ..., n

• по относительным разностям в виде

(5.8)

Тема 6 Решение нелинейных уравнений

Различают две группы нелинейных уравнений:

- алгебраические, содержащие только алгебраические функции (целые, рациональные, иррациональные):

• трансцендентные (тригонометрические, показательные, логарифмические).

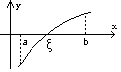F(x) = 0 (6.1)

Корнем (решением) уравнения называется всякое значение ξ, обращающее (6.1) в тождество.

Методы решения нелинейных уравнений:

• прямые, позволяющие записать решение в виде некоторой конечной формулы;

• итерационные, т.е. методы последовательных приближений.

Прямыми методами решают простые уравнения.

Большинство итерационных методов предполагает, что заранее известны некоторые, достаточно малые окрестности, в каждой из которых имеется только один корень.

Т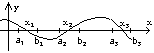 .о. задача приближенного вычисления корней уравнения (6.1) распадается на 2 задачи:

1. задача отделения корней, т.е. отыскания достаточно малых окрестностей, в каждой из которых заключен один и только один корень

2. Вычисление корня с заданной точностью, если известно его начальное приближение в области, не содержащей других корней.