Методы решения слау

Методы решения СЛАУ подразделяются на точные и итерационные.

Точные – это методы, которые определяют решение при помощи конечного числа арифметических операций.

При этом, если исходные данные и вычисления точны, то получается точное решение (методы Крамера, Гаусса).

Точные методы выполняются в два этапа:

• преобразование исходной СЛАУ к более простому виду;

• решение упрощенной системы и получение неизвестных.

Приближенные (итерационные) методы

Предварительно задаются некоторыми приближенными значениями неизвестных , ..., . Из этих значений тем или иным способом получают новые ‘’улучшенные’’ приближенные значения , ..., . С новыми значениями поступают также.

При выполнении определенных условий после бесконечного числа шагов можно получить точное решение.

На практике вычисления прерывают при достижении заданной точности ε. Для этого на каждой итерации с заданной точностью сравнивают два последовательных приближения

Если выполняются условия

, , ... , ,

то полученные на i - итерации значения , ..., считаются решением СЛАУ.

Метод Гаусса

(последовательного приближения неизвестных)

,

где А = ; x = ; b = ;

1. Последовательно исключая неизвестные, приводим матрицу коэффициентов к треугольному виду,

2. Находим неизвестные, начиная с x_n, x_n-1, x_n-2,..., x₂, x₁.

Метод прогонки

(модификация метода Гаусса для систем

с 3-х диагональной матрицей коэффициентов)

, ^{i = 1, 2, ..., n , (4.3)}

Каждое i – уравнение содержит не более 3 неизвестных x_i-1, x_i, x_i+1.

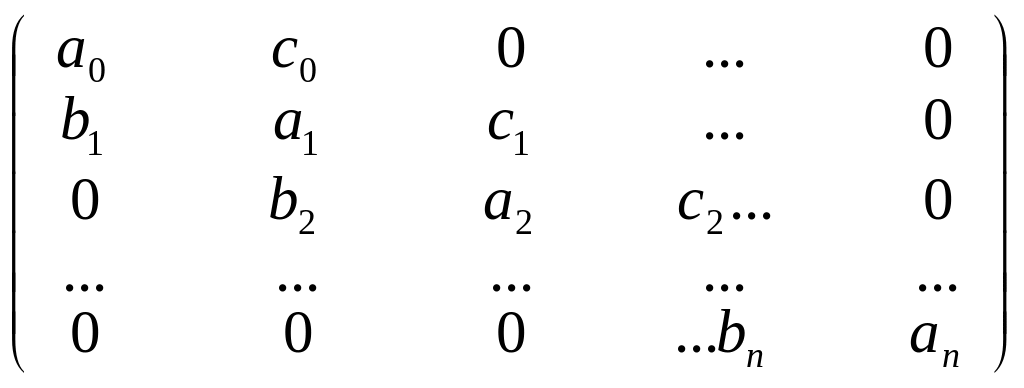; ^(4.4)

Последовательные исключения выполняются так:

Из ''0'' уравнения выражаем и подставляем в 1-е ^{уравнение} .

Затем выразим x₁ через x₂ и подставим во 2-е уравнение и т.д.

Будем считать, что соотношение между x_i и x_i+1 известно

, (4.5)

тогда

(4.6)

Подставим (4.6) в i – уравнение и решим относительно x_i.

.

Выразим (4.7)

Сравнив (4.7) и (4.5), получим прогоночные коэффициенты

, (4.8)

При i = 0 из (4.5) получим .

сравнив с (4.4) получим

, (4.9)

Этапы метода прогонки

1. Прямой ход: каждое i – неизвестное выражается через i+1– е с помощью прогоночных коэффициентов (4.8) и (4.9) (i =0, 1, ..., n-1)

2. Обратный ход: с помощью (4.5) определим x_n , затем

,

и сравним с последним уравнением (4.3).

Выразив x_n ,получим

(4.10)

Далее, используя (4.5) и формулы прогоночных коэффициентов (4.8) и (4.9), находят x_n-1, x_n-2,..., x₁, x₀.