Формулы Ньютона - Котеса

Многие интегралы, не выражающиеся в конечном виде через элементарные функции, представляются быстросходящимися бесконечными рядами.

Вместо подынтегральной функции f(x) интегрируем интерполя-ционный многочлен Лагранжа для равноотстоящих узлов.

h =(b-a) / n.

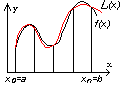
x_i = a + i h, i = 0, 1, ..., n.

y ₀ = f(x₀), y _i = f(x_i), ... , y _n = f(x_n).

, (3.8)

где H_i – весовые коэффициенты (Котеса)

(3.9)

При n = 1 получим формулу метода трапеций, при n = 2 – метода Симпсона.

Для метода трапеций: n = 1, i = 0, 1.

i = 0

i = 1 .

Полученные формулы подставим в (3.8)

Для метода Симпсона: n = 2, i = 0, 1, 2.

i = 0

i = 1

i = 2

После подстановки в (3.8) получим

Основные свойства коэффициентов Котеса

1. Из формулы (3.9) очевидно, что H_i не зависят от промежутка интегрирования и могут быть вычислены раз и навсегда.

2. Вычисления облегчаются благодаря тому, что равноотстоящие от концов коэффициенты H_i равны.

Замечание:

Формулу Ньютона – Котеса лучше применять для нечетного числа узлов, при этом точность повышается.

Тема 4 Решение систем линейных алгебраических уравнений

Рассмотрим систему, состоящую из n уравнений с n неизвестными.

a ₁₁ x ₁ + a₁₂ x ₂ + a₁₃ x ₃ + ... + a_1n x _n = b ₁

a₂₁ x ₁ + a ₂₂ x ₂ + a₂₃ x ₃ + ... + a_2n x _n = b ₂ (4.1)

........................

a_n1 x ₁ + a_n2 x ₂ + a_n3 x ₃ + ... + a_nn x _n = b _n

где x _i – неизвестные, подлежащие определению, a_ij – коэф-фициенты при неизвестных; b _i - числа, называемые свободными членами (правыми частями) системы уравнений.

Форма записи системы (4.1) - скалярная

Совокупность чисел x ₁ = λ₁, x ₂ = λ₂, ..., x _n = λ _n, удовлетворяющих (4.1) называется решением СЛАУ.

СЛАУ называется совместной, если она имеет хотя бы одно решение; в противном случае она называется несовместной.

СЛАУ называется определенной, если это решение - единственное.

Если СЛАУ не имеет ни одного решения, то такая система является неопределенной.

Задача теории систем линейных уравнений состоит в разработке методов, позволяющих узнать:

• совместна ли данная СЛАУ;

• если совместна, то установить число решений;

• указать способ отыскания этих решений.

Матричная форма записи системы (4.1) имеет вид

А = 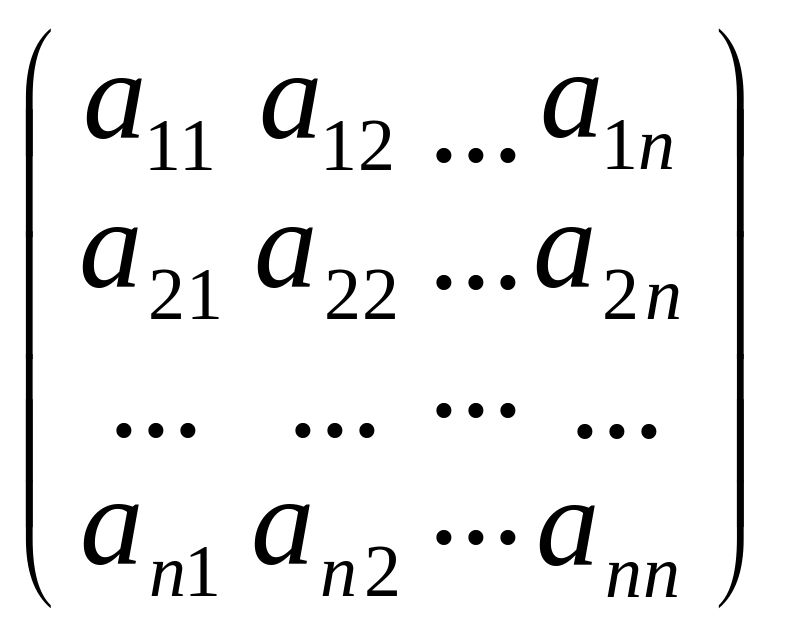; x = ; b = ; (4.2)

Некоторые обозначения:

А^Т – матрица, транспонированная к матрице А, т.е. a _ij = a _ji.

А^-1 – матрица, обратная к матрице А, т.е. А^-1 · А = I,

где I - единичная матрица.

При решении СЛАУ возникают проблемы, связанные с вопросами:

1. разрешима ли данная СЛАУ;

2. каким методом ее решать;

3. какова чувствительность решения к ошибкам округления исходных данных.

Рассмотрим эти вопросы подробнее.

1) Теорема (из курса высшей алгебры)

Система n уравнений с n неизвестными, определитель которой отличен от 0, имеет решение, причем единственное.

(Это условие необходимое, но не достаточное.)

П окажем разрешимость СЛАУ на графике для системы двух уравнений.

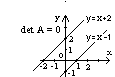det A = 2∙1 – (-2)∙1 = 4 ≠ 0

k₁ = -2, k₂ = 2, k₁ ≠ k₂, т.е. прямые пересекаются

det A = (-1)∙(-1) – 1∙1 = 0

k₁ =1, k₂ = 1, k₁ = k₂, т.е. прямые не пересекаются

2) К выбору методов решения необходимо подходить рационально: например, метод Крамера требует около n²n! операций умножения и деления.

Т.е. для системы с 20 уравнениями и 20 неизвестными это число составляет 10²¹. Для современных ЭВМ, выполняющих миллионы операций в сек., для решения такой системы потребуется около 10¹⁵ сек. или 3∙10⁶ лет.

Следовательно, для систем высокого порядка требуются методы, приводящие к меньшему числу операций.

3) Устойчивость решения относительно погрешностей правых частей и элементов матрицы покажем на примере:

det A = - 0,0001 ≠ 0

точное решение x₁ = 1, x₂ = 1

Если правые части вычислены с незначительной погрешностью, b₁ = 1,989903 и b₂ = 1,970106, то получим решение

x₁ = 3, x₂ = -1,0203.

Такие СЛАУ являются плохо обусловленными.

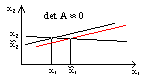
Геометрическая иллюстрация:

Графики прямых этой плохо обусловленной системы почти параллельны. Следовательно, небольшое изменение наклона или сдвиг одной прямой значительно влияет на положение точки пересечения прямых.

Критерий плохой обусловленности

, всегда ≥ 1.

Чем больше , тем хуже обусловлена система ( ≈ 10³ – 10⁴).

На практике обычно проверяют неравенство 0 определителя СЛАУ.