Точность интерполяционных формул

Если функция f(x) является многочленом степени n то в узлах она точно совпадает с интерполяционным многочленом F_n (x).

В общем случае во внеузловых точках разность R (x)=F_n (x) - f(x) отлична от 0 и называется остаточным членом интерполяционной формулы.

В узловых точках R (x_i) = F_n (x_i) - f(x_i) = 0

Пусть f(x) непрерывна и имеет непрерывные производные до n+1 порядка.

Тогда остаточный член

(2.12)

где .

Существует ряд интерполяционных формул Бесселя, Стирлинга, Эверетта, Гаусса и др.

Тема 3 Численное интегрирование

Геометрическое истолкование определенного интеграла: интеграл численно равен площади, покрываемой ординатами графика f(x), т.е. площади криволинейной трапеции, ограниченной осью абсцисс, отрезками прямой x = a, x = b и графиком подынтегральной функции.

,

где F – первообразная.

Если первообразную найти сложно или невозможно, а также, если f(x) задана таблично или графиком, применяется численное интегрирование.

Формула прямоугольников

Промежуток интегрирования [a, b] делим точками x_1, x_2, ..., x_n-1 на n равных частей; длина каждой

h=(b-a)/n.

Т.е. x₀ = a , x_n = b, x_i = a + i h, i = 0, 1, ..., n..

Пусть y ₀ = f(x₀), y _i = f(x_i), ... , y _n = f(x_n).

I ≈ (b - a) f(a) – формула левых прямоугольников

I ≈ (b - a) f(b) - формула правых прямоугольников.

(3.1)

(3.2)

Выражения (3.1), (3.2) дают площади ступенчатых фигур.

Точность формул увеличивается с увеличением n.

Предельная абсолютная погрешность

(3.3)

Формула трапеций

Промежуток интегрирования [a, b] делим точками x_1, x_2, ..., x_n-1 на n равных частей; длина каждой h=(b-a) / n,

Т.е. x₀ =a , x_n b, x_i = a + i h, i = 0,1, ..., n..

Пусть y ₀ = f(x₀), y _i = f(x_i), ... , y _n = f(x_n).

– формула трапеций

(3.4)

Выражение (3.4) дает общую площадь трапеций.

Предельная абсолютная погрешность

(3.5)

Формула Симпсона (параболических трапеций)

Вершины трех соседних точек соединяются дугой квадратной параболы.

Ф ормула площади параболической трапеций

,

Количество точек - 2n

П ромежуток интегрирования [a, b] делим точками x_1, x_2, ..., x_2n-1 на 2n равных частей; длина каждой h=(b-a) / (2n),

x₀ = a , x_2n = b, x_i = a + i h, i = 0, 1, ..., 2n..

Пусть y₀ = f(x₀), y_i = f(x_i),..., y_2n = (x_2n).

, (3.6)

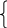г де с = .

Формула (3.6) дает точные результаты для полиномов не выше 3-ей степени.

Предельная абсолютная погрешность

(3.7)

Оценка погрешности

Формулы (3.3), (3.5), (3.7) – 2-го и 4-го порядка точности можно применять, если существует и достаточно легко вычисляются (оцениваются) производные.

На практике, т.к. это бывает редко, применяется ''двойной просчет''.

Допустим, интеграл вычислен дважды при различных значениях шага (h и h / 2).

Пусть интеграл I_n вычислен при h, I_2n – при h / 2.

;

Остаточные члены ; ,

где - среднее арифметическое разностей соответствующего порядка.

Шаг интегрирования выбирается так, чтобы выполнялось неравенство

, (ε задано).