10.8 Символьне розв’язування нелінійних рівнянь

Для одержання розв’язку нелінійного рівняння f(x)=0 у символьному вигляді (тобто, аналітичного розв’язку) можна використовувати один із таких способів:

1) записати вираз f(x), виділити змінну х і відпрацювати пункти меню Символика, Переменная, Решить;

2) за допомогою математичної палітри Символьная ввести шаблон , на місці чорного прямокутника записати вираз f(x), потім клацнути мишею поза межами шаблона.

Як наслідок будь-якої з цих дій з'явиться вектор коренів рівняння (див. приклади на рисунку 10.12). Зауважимо, що в останньому прикладі після одержання символьного розв’язку був застосований ще оператор виведення, що дозволило перейти до наближеного розв’язку у вигляді десяткового дробу.

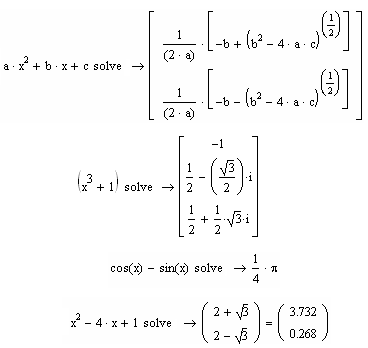
Рисунок 10.12 - Приклади розв’язування нелінійних рівнянь

З наведених прикладів ясно, що розв’язок рівнянь у символьному вигляді має сенс насамперед тоді, коли в рівняннях є параметри (можна одержати розв’язок в узагальненому вигляді, а потім вже обчислювати значення коренів при конкретних значеннях параметрів).

Окрім того, розв’язуючи рівняння у символьному вигляді, користу­вач має можливість знайти точні розв’язки конкретних рівнянь, вира­жені через радикали, комплексні числа або ірраціональні числа типу .

10.9 Чисельне розв’язування рівнянь

Як відомо, багато рівнянь і системи рівнянь не мають аналітичних (тобто представлених в символьному вигляді) розв’язків. У першу чергу це стосується більшості трансцендентних рівнянь. Однак такі рівняння можуть вирішуватися чисельними методами з заданою точністю.

Для найпростіших рівнянь виду f(x) = 0 числове рішення в Mathcad знаходиться за допомогою функції root . Загальний вид цієї функції:

root( f(х), х, a, b )

Функція повертає значення х, що належить відрізку [a, b], при якому вираз або функція f(х) набуває значення 0. Змінній х перед використанням функції root необхідно присвоїти числове значення. Mathcad використовує його як початкове наближення при пошуку кореня. Параметри a, b - необов'язкові, але якщо використовуються, то повинні бути дійсними числами, причому a < b. При заданих значеннях a, b корені рівняння за межами відрізку не визначаються.

Р івняння може мати кілька коренів (див. приклади на рис. 10.13), тоді функція знаходить один з них, як правило той, який ближче до заданого початкового наближення.

Рисунок 10.13 - Приклади використання функції root

Наближені значення коренів можуть бути відомі з фізичного смислу задачі або ж знайдені попередньо, наприклад, графічним способом.

Я

Can’t converge to a solution

кщо після багатьох ітерацій Mathcad не знаходить підхожого наближення, то з'явиться повідомлення (відсутня збіж­ність). Це означає, що початкове наближення обране невірно або ж рівняння взагалі не має коренів.

Для запобігання таких помилок бажано попередньо дослідити графік f(x). Це допоможе з'ясувати наявність коренів рівняння f(x) = 0 і, якщо вони є, то визначити приблизно їх значення. Чим точніше обрано початкове наближення кореня, тим швидше сходиться ітераційний процес визначення кореня з заданою точністю.

Числове значення кореня рівняння є наближеним, його похибка не перевищує заданого значення системної змінної TOL. Для зміни точності, з яким функція root шукає корінь, потрібно змінити значення системної змінної TOL. Для цього слід відпрацювати команді меню Инструменты і Параметры рабочего листа, а потім на вкладці Встроенные переменные встановити в вікні Допустимая сходимость (TOL) потрібне значення. Описане визначення TOL є глобальним, тобто діє для всього документа. Якщо ж потрібно змінити точність в конкретному місці документа, то використовується звичайне присвоєння типу TOL:=0.0001. При збільшенні TOL функція root швидше відшукає наближене значення одного з коренів, але відповідь буде менш точною. Якщо ж значення TOL зменшити, то функція root буде сходитися повільніше, але відповідь буде більш точною.

Зауважимо, що для знаходження коренів полінома виду

a_nxⁿ + ... + a₂x² + a₁x + a₀,

краще використовувати функцію polyroots, ніж root. На відміну від функції root, функція polyroots не вимагає початкового наближення і повертає відразу всі корені, як дійсні, так і комплексні. Загальний вид функції:

polyroots(А)

Функція повертає вектор довжини n, що складає з коренів полінома. Коефіцієнти полінома знаходяться у векторі А довжини n+1. Цей вектор зручно створювати, використовуючи пункти меню Символика і Полиномиальные коэффициенты.