Самостійна робота №21. Розв’язування систем способом додавання

I Варіант

1°. Якщо в системі додати почленно ліві та праві частини рівнянь, то одержимо рівняння...

а) 5x + 22 = 0; б) 10y = 22; в) 11x = 22; г) 5x = 6.

2°. На яке число потрібно помножити обидві частини першого рівняння системи щоб одержати в рівняннях протилежні коефіцієнти при змінній y?

а) 3; б) –3; в) 2; г) 5.

3°. Розв’язати систему рівнянь способом додавання.

4^. Розв’язати систему рівнянь способом додавання:

а)  б) 

5^. Розв’язати систему рівнянь

II Варіант

1°. Якщо в системі додати почленно ліві та праві частини рівнянь, то одержимо рівняння...

а) 8x = 30; б) 10y = 42; в) 10y = –30; г) 7xy = –36.

2°. На яке число потрібно помножити обидві частини першого рівняння системи щоб одержати в рівняннях протилежні коефіцієнти при змінній y?

а) 2; б) –2; в) 3; г) –3.

3°. Розв’язати систему рівнянь способом додавання.

4^. Розв’язати систему рівнянь способом додавання:

а)  б) 

5^. Розв’язати систему рівнянь

III Варіант

1°. Якщо в системі додати почленно ліві та праві частини рівнянь, то одержимо рівняння:

а) 18x = 21; б) 7y = 21; в) y = 11; г) 13xy = 16.

2°. На яке число потрібно помножити обидві частини першого рівняння системи щоб одержати у рівняннях протилежні коефіцієнти при змінній x:

а) –5; б) 5; в) 4; г) –4.

3°. Розв’язати систему рівнянь способом додавання.

4^. Розв’язати систему рівнянь способом додавання:

а)  б) 

5^. Розв’язати систему рівнянь

IV Варіант

1°. Якщо в системі додати почленно ліві та праві частини рівнянь, то одержимо рівняння:

а) 9x = 36; б) 7xy = 16; в) 6y = 36; г) 9x = 4.

2°. На яке число потрібно помножити обидві частини першого рівняння системи щоб одержати у рівняннях протилежні коефіцієнти при змінній x:

а) 2; б) –2; в) 3; г) –3.

3°. Розв’язати систему рівнянь способом додавання.

4^. Розв’язати систему рівнянь способом додавання:

а)  б) 

5^. Розв’язати систему рівнянь

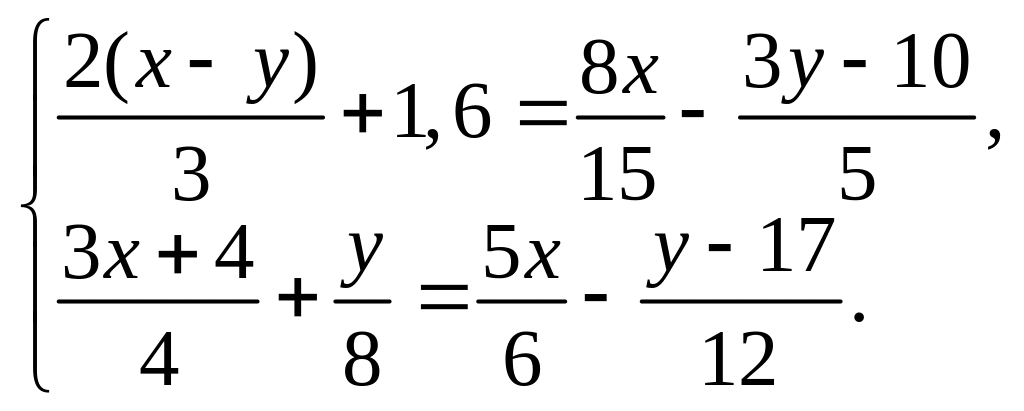
V Варіант

Початковий рівень

1. Яке рівняння одержимо, якщо в рівнянні 2x – 3y = 1 ліву та праву частини помножимо на 5?

а) 5x – 3y = 1; б) 10x – 3y = 5; в) 10x – 15y = 1; г) 10x – 15y = 5.

2. На яке число потрібно помножити обидві частини першого рівняння системи щоб одержати у рівняннях протилежні коефіцієнти при змінній y?

а) 2; б) –2; в) 4; г) –4.

3. Якщо в системі додати почленно ліві та праві частини рівнянь, то одержимо...

а) 4x = 18; б) –2y = 18; в) 12y = 18; г) 2y = 18.

4. Завершити розв’язання системи рівнянь способом додавання:

а) (1; 4); б) (2; 3); в) (4; 1); г) (5; 3).

Середній рівень

1. Помножити перше рівняння системи на деяке число так, щоб при додаванні рівнянь системи отримати рівняння з однією змінною.

2. Розв’язати систему рівнянь способом додавання.

3. Розв’язати способом додавання систему рівнянь виключивши змінну y.

4. Розв’язати систему рівнянь

Достатній рівень

1. Розв’язати способом додавання систему рівнянь:

а)  б)  в) 

Високий рівень

1. Розв’язати способом додавання систему рівнянь:

а)  б) 

2. Розв’язати рівняння (3x – y – 2)² + (5x +y – 6)⁴ = 0.

3*. Розв’язати систему трьох рівнянь із трьома невідомими.

VI Варіант

Початковий рівень

1. Яке рівняння одержимо, якщо в рівнянні 4x – 2y = 5 ліву та праву частини помножимо на 5?

а) 5x – 2y = 25; б) 20x – 10y = 25; в) 20x – 2y = 25; г) 20x – 10y = 5.

2. На яке число потрібно помножити обидві частини першого рівняння системи щоб одержати у рівняннях протилежні коефіцієнти при змінній x?

а) 5; б) –5; в) 6; г) –6.

3. Якщо в системі додати почленно ліві та праві частини рівнянь, то одержимо...

а) 2x = 16; б) 8x = 16; в) 8x = 2; г) 12y = 16.

4. Завершити розв’язання системи рівнянь способом додавання:

а) (5; 3); б) (3; 5); в) (8; 2); г) (4; 2).

Середній рівень

1. Помножити перше рівняння системи на деяке число так, щоб при додаванні рівнянь системи отримати рівняння з однією змінною.

2. Розв’язати систему рівнянь способом додавання.

3. Розв’язати способом додавання систему рівнянь виключивши змінну y.

4. Розв’язати систему рівнянь

Достатній рівень

1. Розв’язати способом додавання систему рівнянь:

а)  б)  в) 

Високий рівень

1. Розв’язати способом додавання систему рівнянь:

а)  б) 

2. Розв’язати рівняння (x – y – 1)⁶ + (2x + y – 8)² = 0.

3*. Розв’язати систему трьох рівнянь із трьома невідомими.

Самостійна робота №22. Розв’язування задач за допомогою системи рівнянь

I Варіант

1°. Сума двох чисел дорівнює 81, а їх різниця — 15. Яка із систем рівнянь відповідає цим умовам, якщо більше число позначили через x, а менше — через y?

а)  б)  в)  г) 

2°. Скласти систему рівнянь для розв’язання задачі.

Булочка дорожча, ніж пиріжок, на 30 к. За 4 булочки та 3 пиріжки заплатили 4 грн. Скільки коштує одна булочка і скільки один пиріжок?

3^. Розв’язати задачу за допомогою системи рівнянь.

Два робітники виготовили разом 1020 деталей. Перший робітник працював 15 днів, а другий — 14 днів. Скільки деталей виготовляв кожний робітник щодня, якщо перший робітник за 3 дні виготовив на 60 деталей більше, ніж другий за 2 дні?

4^. У двох баках було 140 л води. Коли з першого бака взяли 26 л води, а з другого — 60 л, то в першому баці залишилось удвічі більше води, ніж у другому. Скільки літрів води було в кожному баці спочатку?

II Варіант

1°. Перше число на 20 менше від другого, а їх сума дорівнює 60. Яка із систем рівнянь відповідає цим умовам, якщо менше число позначили через x, а більше — через y?

а)  б)  в)  г) 

2°. Скласти систему рівнянь для розв’язання задачі.

1 кг апельсинів дешевший, ніж 1 кг лимонів, на 1 грн. За 2 кг апельсинів і 3 кг лимонів заплатили 28 грн. Скільки коштує 1 кг лимонів і скільки 1 кг апельсинів?

3^. Розв’язати задачу за допомогою системи рівнянь.

Два трактористи заборонували разом 678 га поля. Перший тракторист працював 8 днів, а другий — 11 днів. Скільки гектарів боронував щодня кожний тракторист, якщо перший за 3 дні заборонував на 22 га менше, ніж другий за 4 дні?

4^. У першому бідоні на 5 л молока більше, ніж у другому. Якщо з першого бідона перелити в другий 8 л молока, то в другому бідоні молока стане удвічі більше, ніж залишиться в першому. Скільки літрів молока було в кожному бідоні спочатку?

III варіант

1°. Сума двох чисел дорівнює 15 і одне з них у 4 рази менше від іншого. Яка із систем відповідає цим умовам, якщо більше число позначили через x, а менше — через y?

а)  б)  в)  г) 

2°. Скласти систему рівнянь до задачі.

Оленка заплатила 3 грн. за 3 зошити та 2 олівці, а за такі ж 4 олівці та 1 зошит Сашко заплатив 2 грн. Скільки коштує один зошит і скільки один олівець?

3^. Розв’язати задачу за допомогою системи рівнянь.

Відстань між двома пристанями на річці дорівнює 60 км. Цю відстань за течією ріки катер проходить за 2 год, а проти течії — за 3 год. Знайти власну швидкість руху катера та швидкість течії ріки.

4^. Дві бригади разом повинні виготовити 270 деталей. До середини дня перша бригада виконала 60% свого завдання, а друга — 70% свого, до того ж перша бригада виготовила на 6 деталей більше, ніж друга. Скільки деталей повинна виготовити кожна бригада?

IV Варіант

1°. Різниця двох чисел дорівнює 12 і одне з них утричі більше від іншого. Яка із систем відповідає цим умовам, якщо більше число позначили через x, а менше — через y?

а)  б)  в)  г) 

2°. Скласти систему рівнянь до задачі.

Два токарі виготовили 72 деталі, до того ж перший працював 3 год, а другий — 4 год. Якби перший працював 1 год, а другий — 2 год, то вони виготовили б 30 деталей. Скільки деталей щогодини виготовляв кожен токар?

3^. Розв’язати задачу за допомогою системи рівнянь.

Відстань між двома селищами, що розміщені на березі річки, дорівнює 32 км. Човен може проплисти цю відстань за 4 год за течією річки і за 8 год проти течії. Знайти власну швидкість човна та швидкість течії ріки.

4^. У першому рукописі на 60 сторінок більше, ніж у другому. Друкарка, яка працювала з першим рукописом і виконала 60% своєї роботи, надрукувала на 12 сторінок менше, ніж друкарка, яка працювала з другим рукописом і виконала 80% своєї роботи. Скільки сторінок у кожному рукописі?

V Варіант