Початковий рівень

1. Яка з наведених систем є системою двох лінійних рівнянь із двома змінними?

а)  б)  в)  г) 

2. Яка з пар чисел є розв’язком системи рівнянь

а) (1; 2); б) (1; 1); в) (1; –1); г) (0; 3)?

3 . Скільки розв’язків має система, графіки рівнянь якої зображено на рисунку?

а) Безліч; б) два; в) один; г) жодного.

4. Яке з рівнянь одержимо, якщо в системі рівнянь з першого рівняння виразимо змінну x через змінну y: x = 1 – y і підставимо відповідний вираз замість x у друге рівняння?

а) y – 1 – 2y = 6; б) 2 – y = 6; в) 1 – y – 2y = 6; г) –1 – y – 2y = 6.

Середній рівень

1. Розв’язати графічно систему рівнянь

2. Розв’язати систему рівнянь способом підстановки:

а)  б) 

3. Не виконуючи побудови, знайти координати точки перетину графіків рівнянь y + x = 4 і 2x + 3y = 6.

Достатній рівень

1. Показати графічно, що система рівнянь не має розв’язку.

2. Розв’язати систему рівнянь способом підстановки:

а)  б) 

3. Скласти систему рівнянь, що має розв’язок (–4; 3).

Високий рівень

1. Розв’язати графічно систему рівнянь

2. Розв’язати рівняння |x – y – 1| + x² + 2xy + y²= 0.

3. Знайти значення x та y, за яких вираз буде меншим від виразу на 2, а вираз буде більшим від виразу на 1?

VI Варіант

Початковий рівень

1. Яка з наведених систем є системою двох лінійних рівнянь із двома змінними?

а)  б)  в)  г) 

2. Яка з пар чисел є розв’язком системи рівнянь

а) (7; 0); б) (2; 4); в) (5; –2); г) (5; 2)?

3 . Скільки розв’язків має система, графіки рівнянь якої зображено на рисунку?

а) Один; б) жодного; в) безліч; г) два.

4. Яке з рівнянь одержимо, якщо в системі рівнянь з першого рівняння виразимо змінну x через змінну y: x = 3 + y і підставимо відповідний вираз замість x у друге рівняння:

а) 3y + 3 – y = –5; б) 3 + y = –5; в) 3(y + 3) + y + 3 = –5; г) 3y + 3 + y = –5.

Середній рівень

1. Розв’язати графічно систему рівнянь

2. Розв’язати систему рівнянь способом підстановки:

а)  б) 

3. Не виконуючи побудови, знайти координати точки перетину графіків рівнянь x – y = 2 і 4x + 3y = 15.

Достатній рівень

1. Показати графічно, що система рівнянь має єдиний розв’язок.

2. Розв’язати систему рівнянь способом підстановки:

а)  б) 

3. Скласти систему рівнянь, що має розв’язок (2; –5).

Високий рівень

1. Розв’язати графічно систему рівнянь

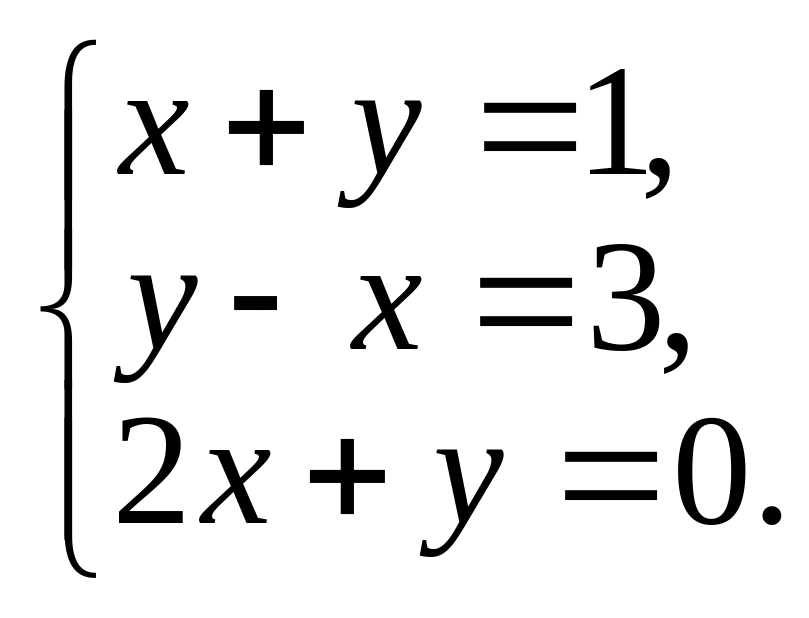
2. Розв’язати рівняння x² – 2xy + y² + |y + x – 2| = 0.

3. Знайти значення x та y, за яких вираз буде удвічі більшим від виразу y – 1, а різниця виразів і дорівнюватиме виразу ?

Контрольна робота №8. Лінійні рівняння з двома змінними. Системи лінійних рівнянь із двома змінними. Графічний спосіб і спосіб підстановки розв’язування систем

I Варіант

1°. Через яку з даних точок проходить графік рівняння 3x + y = 7?

а) A(–2; –1); б) B(–2; 1); в) C(0; 7); г) D(7; 0).

2°. Виразити з рівняння x + 6y = 10 змінну x через змінну y.

а) x = 10 + 6y; б) x = 6y – 10; в) x = 10 – 6y; г) 6y = 10 – x.

3°. Побудувати графік рівняння 5y + x = 2.

4°. Не виконуючи побудови, знайти координати точки перетину графіків рівнянь x + 2y = 5 і 2x – y = 5.

5°. Розв’язати систему рівнянь способом підстановки.

6^. Показати, що система рівнянь має єдиний розв’язок.

7^. Знайти будь-які два розв’язки рівняння .

8*. Побудувати графік рівняння (x + 2)(y – 5) = 0.

II Варіант

1°. Через яку з даних точок проходить графік рівняння 5y – x = 4?

а) F(0; 4); б) K(4; 0); в) D(–4; 0); г) M(–1; 1).

2°. Виразити з рівняння 9y – x = 5 змінну x через змінну y.

а) x = 5 – 9y; б) x = 9y – 5; в) x = –5 – 9y; г) 9y = x + 5.

3°. Побудувати графік рівняння 6x – y = 8.

4°. Не виконуючи побудови, знайти координати точки перетину графіків рівнянь 3x + y = 2 і x + 2y = –6.

5°. Розв’язати систему рівнянь способом підстановки.

6^. Показати, що система рівнянь має єдиний розв’язок.

7^. Знайти будь-які два розв’язки рівняння .

8*. Побудувати графік рівняння |x – 3| + |y + 12| = 0.

III Варіант

1°. Розв’язком якого рівняння є пара чисел (1; 2)?

а) 4x + y = 9; б) 4x – y = 2; в) 3x – 2y = 1; г) 2x + y = 6.

2°. Виразити з рівняння 7x + y = 12 змінну y через змінну x.

а) y = 12 + 7x; б) y = 7x – 12; в) 7x = 12 – y; г) y = 12 – 7x.

3°. Знайти два будь-які розв’язки рівняння 10x + y = 9.

4°. Розв’язати графічно систему рівнянь

5°. Розв’язати систему рівнянь способом підстановки.

6^. Показати, що система рівнянь має єдиний розв’язок.

7^. Знайти ординату точки B, абсциса якої дорівнює 6, якщо через неї проходить графік рівняння  – 5y = 3.

8*. Побудувати графік рівняння |x – y – 1| + x² + 2xy + y² = 0.

IV Варіант

1°. Розв’язком якого рівняння є пара чисел (1; 2)?

а) x – 4y = –7; б) x – 4y = 7; в) 2x – y = 1; г) y – 3x = 1.

2°. Виразити з рівняння y – 12x = 17 змінну y через змінну x.

а) y = 17 + 12x; б) y = –12x + 17; в) y = –12x – 17; г) 12x = y – 17.

3°. Знайти два будь-які розв’язки рівняння x + 11y = 6.

4°. Розв’язати графічно систему рівнянь

5°. Розв’язати систему рівнянь способом підстановки.

6^. Показати, що система рівнянь має єдиний розв’язок.

7^. Знайти ординату точки B, абсциса якої дорівнює 3, якщо через неї проходить графік рівняння 5x – 3y = 13.

8*. Побудувати графік рівняння x² – 2xy + y² + |y + x – 2| = 0.