Лепихин А.П., Богомолов А.В.

Горный институт УрО РАН

Камский филиал ФГУП РосНИИВХ

Оценка коэффициента Шези: традиция и современное состояние1

Аннотация

Рассмотрена особенность задания коэффициентов Шези для русловых потоков. Показано, что большинство традиционных методов оценки данного коэффициента дают, для безгрядового режима, весьма близкие результаты. Ситуация значительно усложняется при грядовом режим, так этом случаи необходимо учитывать в числе определяющих параметров показатель устойчивости частиц. Дан анализ современных подходов к оценке рассматриваемых при грядовом режиме. Продемонстрировано, что структура данных коэффициентов очень существенно влияет на характер гидроморфологическихпараметров русловых потоков.

Estimation of factor of Chezy: tradition and the present

Annotation

The task of Chezyconstant for river streams. Have come to a conclusion that for a river mode without ripples the majority of traditional methods of an estimation of the given factor is yielded by rather close results. A river mode with ripples is very difficult for an estimation. It needs to consider an indicator of stability of a channel. The article have analysis of the modern methods of an estimation ripples river mode. The structure of the given factors very essentially influences character of hydromorphological parametersof river streams.

Введение

Коэффициент Шези занимает центральное место в динамике русловых потоков, являясь ключевым параметром в установленной связи между морфометрическими и динамическими характеристиками руслового потока. По оценке К.В. Гришанина[ 1 ], уже к 30-м годам 20 века, было предложено более 200 различных зависимостей для оценки этого коэффициента, этот процесс достаточно интенсивно продолжается и в настоящее время [2,3,4,5] и др. Для того чтобы достаточно аргументировано ответить на вопрос, чем определяется такое многообразие предлагаемых зависимостей для оценки рассматриваемого коэффициента, необходимо, в первую очередь, рассмотреть основные факторы, определяющие гидравлическое сопротивление русловых потоков.

Антуан Шези[6], занимаясь расчетами параметров канала для обеспечения водоснабжения г. Парижа в 1775г., принимая, что гидравлическое сопротивление потока пропорционально квадрату скорости, установил, что частное скоростей течения двух водотоков должно относится как

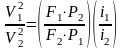
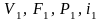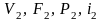где - соответственно, средняя скорость течения по сечению потока, площадь поперечного сечения, смоченный периметр и гидравлический уклон первого и - второго водотока, откуда следует, что , где - гидравлический радиус. Параметр пропорциональности С получил название коэффициента Шези.

Дю Бюа[7] в 1779г., рассматривая общие принципы гидравлики русловых потоков, принимая, что основной силой определяющей движение жидкости в водотоках является сила тяжести, а гидравлическое сопротивление пропорционально квадрату скорости, совершенно независимо от А. Шези получил аналогичное соотношение

. (1)

При этом нетрудно видеть, что .

Запись данного уравнения в форме дю Бюа значительно более корректна, однако, в большинстве учебников и справочников по речной гидравлике пропагандируется, в силу традиций, запись в форме Шези.

Как А. Шези, так и дю Бюа понимали, что коэффициент не может быть постоянной величиной и зависит от морфометрических характеристик водотока.

На протяжении более чем 200 лет очень большое количество исследователей активно занимались установлением этих весьма актуальных для речной гидравлики зависимостей.

Еще в XIX веке в результате проведенных весьма тщательных экспериментов[6] в трубах и каналах, было зафиксировано, что зависимость силы гидравлического сопротивления F_сопр от скорости течения как в каналах, так и в трубах описывается полиномом второй степени

₍₂₎

При этом, при , а при 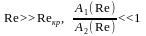, где ( - кинематическая вязкость, Re – число Рейнольдса, характеризующее характер течения в водотоке, при - ламинарный, а если 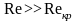- турбулентный).

Проблема осложняется тем, что русловые потоки характеризуются не только очень широким диапазоном изменения как морфометрических, так и динамических параметров потока, но и тем, что в отличие от задачи «трубной» гидравлики, частицы, слагающие донные отложения, способны активно перемещаться и образовывать грядовые структуры, существенно влияющие на формирование гидравлического сопротивления водотоков.

В общем случае, с учетом подвижности частиц донных отложений и способности их формирования в грядовые структуры, обобщим соотношение для условий равномерного установившегося потока (2), рассмотрев полином третьей степени по V

или .

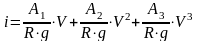Нетрудно видеть, что коэффициенты А₁, А₂, А₃ должны описываться параметрами, определяющими динамику руслового потока. В качестве таких параметров можно принимать - кинематическую вязкость воды, R – гидравлический радиус, g – ускорение свободного падения, d – характерный размер донных отложений, i- гидравлический уклон. При этом необходимо учитывать, что при - русло является гидравлически гладким. В случае, когда 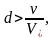находящиеся на дне частицы, слагающие донные отложения: при - неподвижны, а при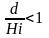 - гидравлически активны.

Исходя из анализа размерности, можно принять:

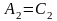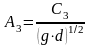, , , при этом С₁, С₂, С₃ - безразмерные константы. Примем, что коэффициенты С₁, С₂, С₃ - полностью автомодельны относительно определяющих их параметров.

В этом случае:

, , .

Записывая уравнение (1) относительно V имеем

.

В общем случае решение уравнения имеет весьма громоздкий вид.

Однако для ряда частных случаев нетрудно получить простые соотношения:

1. При , а также (3)

получаем известное соотношение Стокса для вязкого сопротивления

(4).

Так как требование (3) весьма экзотично для русловых потоков, то данное соотношение может использоваться для гипотетической оценки скорости течения в водотоках при отсутствии турбулентного сопротивления. При использовании стандартной формы записи в виде уравнения ШезиV~C (H*i)^1/2, в этом случае С~ 0,577 Re^1/2по [8];

2. При 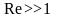и , т.е. дно гидравлически неподвижно,

имеем: (5)

при 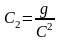,где С - коэффициент Шези. Данное соотношение представляет собой уравнение Шези-дю Бюа.

При , т.е. при гидравлической подвижности дна, имеем

(6).

_Данное соотношение, хорошо согласуется с моделями Lacey [9], А.М. Волынова [5], Д.А. Альтшуля [31] полученными на основе анализа натурных и экспериментальных данных, а так же с результатами работ [10, 11] при _.

При наличии в водотоке грядовых структур необходимо учитывать суммарное эффективное сопротивление, при этом, как правило, используется принцип простой суммации коэффициентов гидравлического сопротивления обусловленных зернистым и грядовым сопротивлением [1,12,13]

_{, (7)}

где - соответственно коэффициент гидравлического сопротивления, обусловленный зернистым и грядовым сопротивлением. Так как 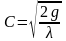, то нетрудно видеть, что

(8)

где 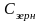, - коэффициенты Шези, обусловленные, соответственно, зернистым и грядовым сопротивлением.

Как следует из (4), включение кинематической вязкости ν может быть эффективно только для ламинарных потоков или для переходной зоны при .

При турбулентном режиме, для гидравлически гладкого русла, единственным определяющим параметром, характеризующим коэффициент гидравлического сопротивления и, соответственно, коэффициент Шези, является число Рейнольдса, . Наиболее известным соотношением, полученным для такого типа русел, является формула Блазиуса, согласно которой: . Таким образом имеем С=28.6 Re^1/8 при Re>10⁵. В тоже время при Re<10⁵ соотношение для С становится неявным[12]:

₍₉₎

Если частицы, определяющие характер смоченного периметра руслового потока неподвижны и их размеры больше толщины вязкого подслоя: 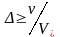, то параметром, определяющим характер коэффициента гидравлического сопротивления, в соответствии с гипотезой, высказанной еще в 1914г. Р. Мизесом, является отношение 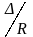, получившее название относительной шероховатости: .

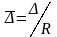Для достаточно строгой оценки коэффициента Шези можно воспользоваться соотношением (2) 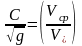, где V_ср – среднее по глубине значение скорости: .

Замена гидравлического радиуса R на глубину среднюю по сечению потока для русловых потоков при не вносит существенной погрешности в гидравлические расчеты.

Таким образом, задачи оценки коэффициента Шези сводится к оценке отношения средней скорости потока к динамической скорости.

Согласно классической логарифмической схеме расчета распределения скорости в в русловом потоке [14]:

, где χ- постоянная Кармана (10)

т.е. принимается, что вертикальный градиент скорости потока полностью автомоделен относительно локального числа РейнольдсаRe_*.

Учитывая (10) для гидравлической шероховатости русла имеем

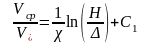
_{. (11)}

Как показал Г.И.Баренблатт [15], если гипотеза по полной автомодельности распределения скорости относительно локального числа Рейнольдса не может быть принята, то в условиях неполной автомодельности имеем

. (12)

Для гидравлически негладкого русла, соответственно, имеем

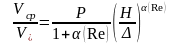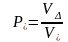, , (13)

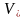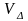где -динамическая скорость потока; - придонная скорость потока.

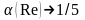К.В. Гришанин [1], используя результаты классических экспериментов И.И. Никурадзе, определил Р_*=7,5. Согласно оценкам В.И. Ефремова Р_*=7,4, в то же время, по экспериментальным данным Ванони Р_*=6,6. Как показано в [15] коэффициент изменяется в зависимости от Re в интервале . При , а при .

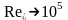
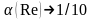Используя соотношение (11) для оценки коэффициент Шези С, имеем

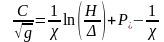, (14)

а при использовании соотношения (10) имеем

_. (15)

Среднее течение равнинных рек характеризуются величиной параметре .

Для удобства дальнейшего анализа введем . Большинство предлагаемых и используемых соотношений для оценки коэффициента С_зерн имеют структуру близкую к соотношениям (14, 15).

Необходимо отметить особенности логарифмической функции:

- в диапазоне значений 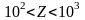она очень близка к степенной функции с показателем степени ;

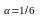- в диапазоне 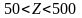- к степенной функции с показателем степени 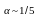_. Таким образом, в рассматриваемом диапазоне и при данных значениях коэффициента α, логарифмические и степенные функции практически тождественны, и, соответственно, зависимости, используемые для оценки коэффициента С, построенные с их использованием так же тождественны.

Достаточно часто для оценки величины донных отложений наряду с характерными размерами донных отложений используется коэффициент «гидравлической шероховатости» - n, имеющий весьма «странную» размерность [сек/м^1/3].

Согласно классической формуле Штриклера

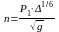или

или в более общем виде

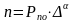_{. (16)}

Соответственно, используя соотношение (11), имеем

, (17)

используя соотношение (17) и учитывая, что

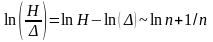(18)

получаем зависимость вида:

(19)

Соотношение (19) аналогично известной формуле Бахметьева –Агроскина.

При , имеем наиболее популярное соотношение для оценки коэффициента Шези, рекомендованное Р. Маннингом и получившее название формула Маннинга. Попытка достаточно строгого обоснования данного соотношения, на основе схемы А.Н. Колмогорова диссипации турбулентной энергии потока , была предпринята в [16]. Н.Н. Павловским рассмотрено и предложено соотношение с переменными значениями коэффициента _.

Сопоставительное представление наиболее распространенных по терминологии [6] ранних формул для оценки коэффициента Шези, дается в таб. 1 и на рис.1.

Таблица 1