В .5. Электрические токи и магнитные потоки в различных физических средах

Полный электрический ток представляет собой скалярную величину, равную сумме тока проводимости, тока переноса и тока смещения сквозь замкнутую поверхность. Познакомимся с этими видами токов и со средами, где они наиболее ярко проявляются.

Электрическим током проводимости называют явление на­правленного движения свободных носителей заряда в веществе или в пустоте. Вещества, обладающие свойством проводить под дей­ствием не изменяющегося по времени электрического поля не из­меняющийся во времени электрический ток, принято называть про­водниками, само это свойство - электропроводностью, а ток i_пр= dq/dt –током проводимости. Хотя ток – величина скалярная, но в разных элементах поверхности S , выделенной в проводнике (рис. В.13), он может иметь свое направление.

Рис.В.13

Таким образом, можно ввести в рассмотрение векторную величину плотность тока, равную пределу отношения тока сквозь элемент поверхности ∆s, нормальный к направлению дви­жения заряженных частиц, к этому элементу, когда последний стремит­ся к нулю J= lim ∆i/∆s =di/ds,(∆s→0) и имеющую направление, совпадающее с направлением движения положительно заряженных частиц или, соответственно, противоположное направлению движения отрицательно заряженных частиц. Если единицей тока служит ампер (1А), то единицей плотности тока – ампер на квадратный метр (А/м²). В изотропной среде(среде, свойчтва которой одинаковы во всех направлениях)вектор плотности тока оказывается пропорциональным вектору напряженности электрического поля J=γĒ.

Э ту зависимость, называемую еще законом Ома в дифферен­циальной форме, записывают еще и в таком виде Ē=ρJ.

Здесь величина γ - удельная электрическая проводимость, ее единицей является сименс на метр (См/м), а ρ - удельное электрическое сопротивление, его единицей является ом-метр (Ом м). Ве­щества, для которых характерен ток проводимости - это металлы (носители тока в них - свободные заряды), уголь и электролиты (в электролитах проводимость обеспечивается положительными и от­рицательными ионами). Если ток проводимости i_пр имеет место в прямолинейном отрезке длиной l и сечением s, то напряжение на этом участке будет u = Еl, а сам ток I = Js. Таким образом, u=ρJl=(ρli): s, а величину R=u/i называют электрическим сопротивлением (для краткости просто сопротивлением) рассмат­риваемого отрезка проводника. Единицей сопротивления является ом (Ом). Соотношения и = Ri или i = Gu называют законом Ома для такого участка проводника, здесь G - проводимость, ее едини­цей является сименс (См). При наличии тока в рассматриваемом проводнике справедливо соотношение р = A/t =(uq)/t = ui-Ri² , называемое законом Джоуля-Ленца. Здесь р - мощность, определяется количеством энергии, выделяемой в проводнике в единицу времени. Единицей мощности служит ватт (Вт).

Специальный элемент электрической цепи, созданный для использования его электрического сопро- тивления, называют резистором. Условное изображение резистора показано на рис. В.14, а его компо- нентное уравнение имеет вид и= Ri .

Рис.В.14

Т оком переноса i_пер называют явление переноса электриче­ских зарядов движущимися в свободном пространстве заряженны­ми частицами или телами. Пример - движение элементарных час­тиц, обладающих зарядом в пустоте, электрический ток в газах, дви­жение заряженных частиц пыли (угольной, мучной и т.д.). Плот­ность этого тока можно описать выражением J = p₊v₊ + p_v_{_}, где р₊ и р_ - объемные плотности положительно и отрицательно заря­женных частиц, аv₊и v_--их соответствующие скорости.

Электрический ток смещения i_см имеет место в диэлектриках при переменных электрических полях, но возникает и в пустоте. Электрическим током смещения называют совокупность элек­трического тока смещения в пустоте и электрического тока по­ляризации. Количественно эта совокупность характеризуется ска­лярной величиной, равной производной по времени от потока элек­трического смещения через замкнутую поверхность. Таким обра­зом, для знакомства с этим видом тока необходимо познакомиться с понятиями поляризации и электрического смещения. Эти понятия не относятся к числу элементарных, и ниже они излагаются не­сколько упрощенно.

В ряде веществ заряды, входящие в состав молекул в отсутст­вие внешнего поля, не создают поля во внешнем по отношению к молекуле пространстве. Дело в том, что центр электрического дей­ствия электронов этих молекул совпадает с центром действия по­ложительных ядер этих молекул. Но при наличии внешнего поля центр положительных и отрицательных зарядов несколько смеща­ется, и во внешнем пространстве молекула будет восприниматься как диполь, т.е. система из двух равных, но противоположных по знаку зарядов +q и -q, расположенных на некотором расстоянии d. Произведение qd называют электрическим моментом диполя. Этот момент можно рассматривать и как векторную величину р, направленную в сторону смещения положительного заряда. Веще­ства с молекулами, рассматриваемыми как диполи, оказываются в поляризованном состоянии. Степень поляризации этих веществ в каждой точке характеризует векторная величина, называемая поляризованностью и обозначаемая буквой Р. Поляризованность рав­на пределу отношения электрического момента некоторого объ­ема вещества, содержащего данную точку, к этому объему, когда последний стремится к нулю. Оказывается, что для интересующей нас группы веществ (см. ниже) поляризованность пропорциональна напряженности поля Р=χĒ; коэффициент χ называется абсо­лютной диэлектрической восприимчивостью вещества.

Вещество, основным электрическим свойством которого яв­ляется способность поляризоваться под действием электрическо­го поля, называется диэлектриком.

О бозначим через D = ε₀Ē + р = D₀ + Р, D₀=ε₀Ē вектор, кото­рый назовем вектором электрического смещения. Для изотроп­ного вещества D = εĒ, где ε - абсолютная диэлектрическая про­ницаемость вещества, и направления векторов D и Ē совпадают. Вектор плотности тока смещения в диэлектрике определяется как

δ_см=dD/dt=dD₀/dt+dP/dt,

г де δсм=dD₀/dt - называют плотностью тока смещения в пустоте. Вторая составляющая в этом выражении J=dP/dt обусловлена движением обладающих зарядом частиц в диэлектрике.

Если теперь обозначить через J_пр, J_nep и δ_см - соответственно плотности токов проводимости, переноса и смещения, а через 8 плотность полного тока (δ = J_np + J_nеp + δ_см), то для полного тока будет справедлив принцип: полный электрический ток сквозь взя­тую в какой угодно среде замкнутую поверхность равен нулю

i = ∫ δ d S = 0.

Таким образом, линии тока не имеют ни начала, ни конца, они принципиально являются замкнутыми линиями. Обратим внимание теперь на связь электрического тока с магнитным по­лем. Этот ток и поле всегда появляются одновременно и, по сути, характеризуют единый физический процесс. Остановимся на этом подробнее, рассмотрев расположенную в пустоте рамку с током i (рис. В. 15), вокруг которой существует магнитное поле. Выберем произвольный замкнутый контур (пунктирная ли­ния на рис. В. 15) и возь­мем интеграл вектора индукции вдоль этого контура.

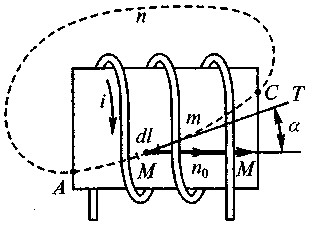
Рис.В.15

При этом оказывает­ся, что ток в рамке и ли­нейный интеграл индук­ции по рассматриваемому контуру связаны соотно­шением

∫ Bdl = ∫ В cos α dl = μ₀i.

Величину μ₀ называют магнитной постоянной, она равна μ₀=4π × 10^-7=1,257 ×10^-6

Гн/м, ее размерность связана с размерностью электрической постоянной, а именно

[μ₀]=[q/ε₀ν²], где [ν]=м/с.

Рассмотрим теперь случай, когда в катушку с током i, имеющую w витков, внесено тело из какого-либо вещества (рис. В. 16).

Рис.В.16

Оказывается, под воздействием магнитного поля, создаваемого током i катушки, вещество намагничивается, т.е. происходит определенная ори­ентация его элементарных то­ков. Такие токи всегда сущест­вуют в веществе (движение электронов по орбитам и внутри ато­мов, или вращение электронов вокруг своих осей), но ориентированы хаотически. В данном случае эта ориентация элементарных электрических токов упорядочивается. Более того, существует та­кая группа веществ - ферромагнетики, в которых элементарные то­ки под действием внешних токов располагаются таким образом, что резко усиливают внешнее поле. Именно на основе таких мате­риалов и реализуются магнитные цепи, которые также будут пред­метом изучения в этой книге.

Рассмотрим механизм взаимодействия магнитного поля с то­ками, в том числе элементарными, подробнее. Составим линейный интеграл вектора магнитной индукции вдоль замкнутого контура, охватывающего витки катушки, намотаннойна цилиндр из интере­сующего нас материала. Тогда вместо тока i рамки (см. рис. В.15) в создании поля участвуют токи wi, создаваемые всеми витками ка­тушки, а также ток i^, - эквивалентирующий элементарные токи на участке. Таким образом

∫ Bdl = μ₀wi + μ₀i^, .

Рассмотрим второе слагаемое правой части этого уравнения подробнее. Пусть

di_, - суммарный элементарный ток на отрезке dl линии АтС. Оказывается, что величина производной этого тока —

d i^,/dl в некотором определенном направлении, которое на рис. В. 16 обо­значено вектором n₀, имеет наибольшее значение. Обозначим отре­зок dl в этом направлении dn и введем векторную величину M= di^,/dn× n₀ , которую назовем намагниченностью вещества. Так как на участке СпА контура интегрирования (рис. В. 16) нет элемен­тарных токов, то

∫ Bdl=∫ Мdl,следовательно

AmCnA AmC

∫ Bdl= μ₀wi + μ₀i^, = μ₀wi + μ₀ ∫ Мdl или ∫ (В/ μ₀-М)dl= wi.

Здесь подынтегральную величину называют напряженностью магнитного поля Н=В/ μ₀-М.

Для изотропного вещества В = μН, где μ = μ₀(1+χ), χ - магнитная восприимчивость, т.е. направления В и Н совпадают.

Т огда ∫ Hdl = 0. Если при этом контур интегрирования охватывает часть проводника с током (рис. В. 17), то выражение

∫ Hdl =i,

где под токами понимаются все токи: проводимости, переноса, смещения, называют законом полного тока, при этом линейный интеграл напряженности магнитного поля называют магнитодвижущей силой (МДС) вдоль этого конту­ра.

Рис.В.17

Магнитодвижущую силу будем обозначать бук­вой F, МДС играет в теории магнитных цепей при­мерно ту же роль, что и ЭДС в теории электрических цепей. МДС вдоль замкнутого контура равна полно­му току, охватываемому этим контуром. Можно рассматривать МДС и применительно к отрезку линии между точками А и В ,

B

тогда F_AB=∫ H dl. Единицей МДС F служит ампер (А), а единицей напряженности Н магнитного

A

поля - ампер на метр (А/м