В.З. Электрическое напряжение, электрический потенциал, электродвижущая сила, источник эдс, электрическая емкость, конденсатор

Познакомимся с рядом понятий, связанных с электрическим полем и являющихся фундаментальными понятиями для теории электрических цепей.

Пусть частица с зарядом q пере­носится в электрическом поле из точки А в точку В вдоль некоторого пути (рис. В.6).

Рис.В.6

Действующие на нее силы совер­шают работу А, величина которой пропорциональна заряду q; а именно A = qU_AB, где величину U_Ав называ­ют электрическим напряжением.

Э лектрическое напряжение - это физическая величина, ха­рактеризующая электрическое поле вдоль рассматриваемого пу­ти и равная линейному интегралу напряженности электрическо­го

В

п оля вдоль рассматриваемого пути. В нашем случае (см. рис. В.6) U_ab=∫ Ēdl. Заметим, что в электри ч еском поле интеграл не зависит от выбора пути между точками А и В, т.е.∫ Ēdl = ∫ Ēdl (рис. В.7),

АnB AmB

и соответственно ∫ Ēdl = ∫ Ēdl =0

AnBmA

Рис.В.7

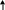
При этом величину, равную этому интегралу, называют разно­стью электрических потенциалов точек А и В и обозначают

в

U_AB = V_A-V_B = ∫ Ēdl .

A

В электрическом поле понятие напряжения между двумя точ­ками тождественно понятию разности потенциалов U_AB = V_A-V_B. При этом, если в поле выбрана некоторая особая точка Р (часто

Р

это бесконечно удаленная точка), тогда значение интеграла ∫ Ēdl является

А

только функцией координат (х, у, z) точки А.

P

Обозначив эту функцию через V_A, можно записать ∫ Ēdl =V _{A =}V(x, у, z).

A

Величину V_A называют электрическим потенциалом

т очки А. По­тенциал же особой точки Р, очевидно, равен нулю, т.к. V_P=∫ Ēdl=0. На практике равным нулю обычно прин имают потенциал поверхности земли, а не бесконечно удаленной точки, как в теории. Заметим, что если в электрическом поле потенциал каж­дой точки А определяется после выбора особой точки Р, то такое поле называют потенциальным полем. В потенциальных полях линейный интеграл напряженности электрического поля по лю­бому замкнутому контуру равен нулю. Однако это не относится к областям пространства, в которых расположены так называемые источники электродвижущих сил - сокращенно ЭДС. В облас­тях пространства, заключающих такие источники, электрические поля носят не потенциальный характер. Возникновение ЭДС обу­словлено наличием в соответствующих областях пространства электрических полей не потенциального характера. Говорят, что в замкнутом контуре действует электродвижущая сила е, если ли­нейный интеграл напряженности электрического поля по этому контуру не равен нулю; причем величину ЭДС полагают равной этому интегралу, т.е.

е = ∫ Ēdl ≠0.

П одобное оказывается возможным, когда наряду с потенци­альным полем с напряженностью Ē_пот в этих областях имеется стороннее электрическое поле с соответствующей сторонней на­пряженностью Ē _стор и сторонней силой f_стор, действующей на за­ряды. Именно сторонние силы совершают работу по переносу за­рядов, что и обеспечивает появление ЭДС е = е_стор:

е = ∫ Ēdl = ∫ (Ē _пот +Ē _стор)dl= ∫ Ē _стор dl ≠0;

з десь ∫ Ē_пот dl =0. Эти сторонние силы могут быть обусловлены электрохимическими, электротермическими, электромеханическими и т.д. процессами. В технике создают специальные устройства (ак­кумуляторы, генераторы и т. д.) с локализованными в ограниченных областях сторонними полями, которые называют источники ЭДС или в общем случае - источники энергии. Таким образом, в этих источниках происходит преобразование энергии химических про­цессов («химической энергии»), энергии заметить из представлен­ных выше выражений, если подобный источник в пространстве ло­кализован между двумя точками - точкой А с координатами (x_A,y_A,z_A) и точкой В с координатами (x_B,y_B,z_B) - например, двумя электролитическими аккумуляторами, имеющими соответст­вующие потенциалы V_A=V_A(x_A,y_A,z_A) и V_B =V_B(x_B,y_B,z_B), то электродвижущая сила подобного элемента равна разности по­тенциалов

e=V_A- V_{B .}

Здесь точки Aи В считаются расположенными на границе по­тенциального (вне источника) и не потенциального (внутри источ­ника) полей.

Единицей напряжения, потенциала, разности потенциалов, ЭДС в системе СИ (система интернациональная) принят вольт (Volt), обо­значается 1 В или 1 V. Так разность потенциалов V_А - V_B двух точек А и В потенциального электрического поля (рис. В.6) равна 1 В, если при перемещении заряда в 1 кулон (обозначается 1 Кл) против сил поля необходимо совершить работу в 1 джоуль (1 Дж). Тогда связь электрического напряжения с напряженностью электрического поля

B

U_AB =∫ Ēdl дает единицу напряженности – вольт на метр (1 В/м).

A

При исследовании электрического поля в веществе необхо­димо в полной мере учитывать его электрические свойства. По этим свойствам вещества делят на проводники (проводящие веще­ства), диэлектрики (изолирующие вещества) и полупроводники (полупроводящие вещества). Основной характеристикой провод­ника является электропроводность, т.е. способность проводить электрический ток под действием постоянного электрического поля. В проводниках носители заряда (электроны, а также поло­жительные и от рицательные ионы) находятся в свободном со­стоянии. Под действием электрического поля они приходят в упо­рядоченное движение и образуют электрический ток. В диэлек­триках свободные частицы с зарядами практически отсутствуют, заряды находятся в связанном состоянии, и под действием элек­трического поля происходит лишь поляризация связанных зарядов (положительные и отрицательные частицы, испытывая механиче­ские силы со стороны поля, начинают двигаться, но совершенно разойтись не могут, удерживаемые внутренними силами). Основ­ной характеристикой диэлектрика выступает абсолютная диэлек­трическая проницаемость е, отражающая, в частности, влияние среды на силовые взаимодействия зарядов в законе Кулона (см. выше). Полупроводники занимают некоторое промежуточное по­ложение между проводниками и диэлектриками.

Заметим, что напряженность электрического поля внутри про­водников в статическом состоянии зарядов может быть равна только нулю Е =0. Иначе был бы ток и, следовательно, состояние зарядов не было бы статическим. Поэтому в электростатическом состоянии проводящее тело имеет один и тот же потенциал (разность потенциалов между его любыми точками равна нулю

B

V _А - V_B =∫ Ēdl=0).

A

Рассмотрим теперь некоторое проводящее тело с зарядом q, окруженное диэлектриком, в предположении, что диэлектрическая постоянная последнего не зависит от напряженности электрическо­го поля. Тогда оказывается, что величина напряженности всюду в диэлектрике и на границе с проводником, в частности, будет про­порциональна заряду тела q, следовательно, пропорциональным за­ряду этого тела окажется и потенциал V тела. Отношение q к V на­зывают электрической емкостью тела и обозначают

C=q/V.

В случае двух таких проводящих тел с равными по величине, но противоположными по знаку зарядами q₁= - q₂, которые окру­жены диэлектриком, электрической емкостью называют величину

C=q₁/V₁-V₂= q₂/V₂-V_1.

Электрическая емкость как уединенного проводящего тела, так и двух проводящих тел зависит от параметров среды (ε), геометрии тел, а в последнем случае и от взаимного расположения. Система двух проводящих тел, специально созданная для использования в практических целях ее емкости, называется конденсатором.

Единицей электрической емкости служит фарада (1 Ф), 1Ф=1Кл/1В.

Конденсатор с заряженными пластинами является носителем электрической энергии. Если напряжение между двумя его обклад­ками равно u= V₁ - V₂, а их заряды равны по величине, но противо­положны по знаку q = q₁= -q₂, то можно показать, что энергия конденсатора равна

W_э=uq/2=Cu²/2=q²/2C.

Конденсатор как элемент электрической цепи принято изо­бражать так, как показано на рис. В.8, а связь между его током и напряжением в случае их изменения во времени (i=i(t), u=u(t))^* , на­зываемую компонентным уравнением, м ожно получить, продифференцировав выражение q=C/u. Таким образом, компонентное уравнение конденсатора имеет вид i=C du/dt , где i=dq/dt.

Рис.В.8

В.4. Магнитный поток, потокосцепление, ЭДС самоиндукции и взаимной индукции, индуктивность и взаимная индуктивность

Познакомимся с рядом понятий, связанных с магнитным полем и являющихся фундаментальными для теории магнитных цепей.

Пусть магнитная индукция В пронизывает некоторую поверх­ность S, образованную тонким проводником l. Тогда интеграл маг­нитной индукции по этой поверхности (рис. В. 9)

∫BdS=∫B cos β dS=Ф

S S

называют потоком магнитной индук­ции и обозначают буквой Ф.

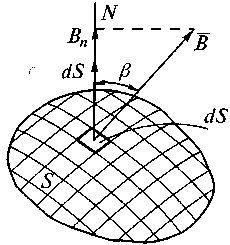
Рис.В.9

Единицей магнитного потока служит вебер (Вб), а единицей магнитной индукции, т.е. плотности этого потока в данной точке, является тесла (Тл). Таким образом 1 Вб=1Тл\м².

Рассмотрим случай, когда поток Ф₁₁ создается собственным током проводника i ₁ контура l₁, (рис. В. 10а), и случай, когда поток Ф₁₂ в первом контуре l₁, есть часть потока, созданного током i₂ второго контура l₂.

Рис. В. 10

Е сли эти потоки Ф₁₁ (рис. В. 10а) и Ф₁₂ (рис. В.10.6) изменя­ются во времени, что можно трактовать как относительное движение самих контуров относительно поля с потоками Ф₁₁, Ф₁₂, то на заряды в проводниках будут действовать силы со стороны магнитного поля (см. раздел В.2), и в контуре l₁ (рис. В. 10б) будет индуцироваться ЭДС Ē_инд . Общее выражение для ее расчета дается за­коном электромагнитной индукции: если магнитный поток Ф, про­ходящий сквозь замкнутую поверхность S , ограниченную конту­ром l (рис. В.11), изменяется во времени, то в этом контуре индук­тируется ЭДС, равная взятой со знаком минус скорости изменения этого потока

E= ∫ Ē_инд × dl=-dФ/dt.

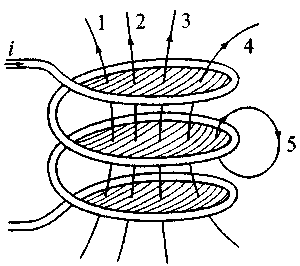
Рис. В.11

Поскольку величина этой ЭДС зависит от потока сквозь замк­нутую поверхность, то эту поверхность стараются сделать слож­ной, придав ей форму многослойной катушки (рис. В.11) с тем, чтобы обеспечить максимальную по величине индуктируемую ЭДС. По­скольку каждое кольцо этой катуш­ки пронизывает почти один и тот же поток (почти, потому что некоторые линии индукции замыкаются и во­круг отдельных колец - см. рис. В.11, линия 5), то вводят понятие о потокосцеплении ψ. Применитель­но к данной катушке можно для уп­рощения положить, что все линии магнитной индукции сцепляются со всеми витками катушки, тогда ψ=wФ, где w-число витков катушки. Тогда для индуктируемой ЭДС имеем

е=-dψ/dt=-w dФ/dt.

В случае, когда ЭДС индуктируется собственным током (см. рис. В. 10а), ее называют электродвижущей силой самоиндукции и обозначают e_L . Потокосцепление катушки при этом называют потокосцеплением самоиндукции и обозначают

ψ_L. Оно оказывается пропорциональным току катушки. Представим его в виде ψ_L=Li .

Величину L называют собственной индуктивностью или индуктивностью, ЭДС самоиндукции при этом имеет вид

E_L=-dψ_L/dt=-d(Li)/dt=-L di/dt – I dL/dt.

Или при наиболее понятном для практики случае L = const имеем e_L=-L di/dt. В частности для контура, изображенного на рис. В. 10а, e_L1=-L₁ i₁/dt.

В случае, когда с рассматриваемым контуром (l₁,рис. В.10б) сцеплен поток (потокосцепление) другого контура (контура l₂, рис. В. 106), говорят о потоке (потокосцеплении) взаимной ин­дукции. Потокосцепление обозначается буквой ψ₁₂ c двумя индекса­ми, первый из которых указывает, с каким контуром рассматрива­ется сцепление потока (у нас с контуром 1), второй индекс (2) пока­зывает, током какого контура создается данное потокосцепление (у нас током второго контура). Потокосцепление также оказывается пропорциональным вызывающему току ψ₁₂=M₁₂ i₂ ,

где величина М₁₂ называется взаимной индуктивностью конту­ров. Заметим, что если бы мы рассматривали поток ψ_2l, сцеплен­ный со второй катушкой и обусловленный током i₁, первой катуш­ки, то величина М ₂₁ из равенства ψ₂₁=M₁₂ i₁ оказалась бы равной величине М₁₂, т.е. М₂₁ =М₁₂ = М. Таким образом, эта величина зависит только от геометрии катушек, их взаимного расположения и параметров среды. Изменение потокосцепления в контуре вызы­вает в нем электродвижущую силу взаимной индукции. Так ЭДС в первом контуре (рис. В. 106), обусловленная изменением тока во втором контуре, может быть представлена как

e₁₂=-dψ₁₂/dt=-d(M₁₂i₂)/dt=-M₁₂ di₂/dt – i₂ dM₁₂ /dt

или при М₁₂=const

e₁₂=-M₁₂ di₂/dt.

Единицей индуктивности и взаимной индуктивности является генри (Гн). Специальный элемент, созданный для использования его ин­дуктивности, носит название индуктивной катушки или просто катушки. Катушка с индуктивностью L и током i (и потокосцеплением ψ=Li) является носителем магнитной энергии, которая в этом случае равна

W_M=1/2 Li² = ψ²_L /2L.

В случае системы из двух контуров с токами i₁, i₂, индуктивностями L₁, L₂ и взаимной индуктивностью М запасенная в них энергия определяется выражением W_M=1/2 L₁i₁²+1/2 L₂i₂² +Mi₁i₂ .

Индуктивную катушку, как элемент электриче­ской цепи, принято изображать в виде, показанном, на рис В. 12. Компонентное уравнение, составляющее связь между током и напряжением катушки, имеет вид u_L=L di/dt, где u=-e_L.

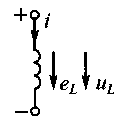
Р ис.В.12