В.2. Электрическое и магнитное поле

При изучении электромагнитных явлений принято выделять две стороны - электрическую и магнитную, между которыми суще­ствует тесная связь. В соответствии с этим выделяют и две стороны электромагнитного поля - электрическое и магнитное поле.

Электрическое поле - это одна из сторон электромагнитного поля, обусловленная электрическими зарядами и изменением магнит­ного поля, оказывающая силовое воздействие на неподвижные заря­женные тела и частицы. Для выявления этого поля необходимо рас­смотреть неподвижное заряженное тело, поскольку на движущееся тело действует не только электрическое, но и магнитное поле.

Исследуем поле некоторого основного тела с зарядом q. Для этого в различные точки окрестности этого тела будем помещать пробное точечное тело (т.е. тело со столь малыми размерами, что в его пределах исследуемое поле можно считать однородным) с поло­жительным зарядом q₀. В каждой точке на пробное тело будет дей­ствовать механическая сила. В случае, когда основное тело так же имеет точечные размеры, величина этой силы определяется по за­кону Кулона

f₁= qq₀ /4πεr² ,

где r - расстояние между зарядами, а ε^* - постоянная, называемая абсолютной диэлектрической проницаемостью, характеризует среду, в которой находятся эти заряды. Рассматриваемая сила по­зволяет определить основную физическую величину, характеризующую электрическое поле и называющую­ся его напряженностью (рис. В.1).

Рис. В.1

Напряженность электрического поля Ē есть векторная величина, сонаправленная с силой f, действующей на неподвижное положительно заряженное пробное тело, помещенное в данную точку поля к величине этого заряда.

Таким образом, Ē=f₁ /q₀

Рассмотренное электрическое поле, обусловленное исключи­тельно неподвижными зарядами, называют так же электростати­ческим полем. Помещая пробный заряд в самые разные точки поля и определяя в них напряженность электрического поля, можно про­вести ряд линий так, чтобы в каждой напряженности электрического поля (рис. В.2). точке линий касательная к ним совпадала по направлению с вектором

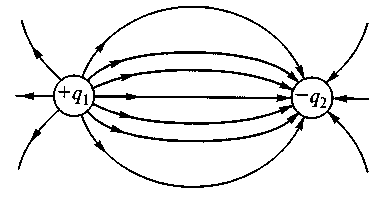
Рис. В.2

Эти линии, являющимися, по сути, силовыми линиями, называют линиями напряженности электриче­ского поля. На рис. В.2 они снабжены стрелками, указы­вающими направление вектора Ē. Совокупность таких линий образует картину электрического поля.

Магнитное поле - одна из двух сторон электромагнитного поля, обусловленная движущимися заряженными частицами и из­менением электрического поля, оказывающая силовое воздействие на движущиеся заряженные частицы, и выявляемая по силовому воздействию, направленному нормально к направлению движения частиц и пропорциональному их скорости.

Эрстедом, а затем Ампером было установлено, что на магнит­ную стрелку, расположенную вблизи проводника с током, оказыва­ется силовое воздействие, в результате которого стрелка ориенти­руется относительно проводника с током вполне определенным образом.

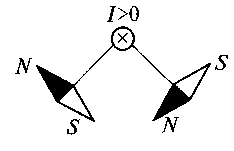
Рис.В.3

На рис. В.3 изображены проводник с постоянным током I , уходящим за плоскость чертежа (что принято отмечать косым крестом), и ориентация расположенной в плоскости чертежа стрелки в магнитном поле такого тока. Для выявления силовой характеристики этой стороны электромагнитного I > 0поля необходимо рассмотреть движущиеся заряды, например, движущиеся по некоторому проводнику длиной l. Напомним, что движение зарядов является электрическим током. Пусть l - вектор, имеющий длину, равную длине отрезка проводника l , и направленный по оси проводника в направлении тока i, a q - заряд в объеме проводника, движущийся вдоль его оси со скоростью v . Если заряд q проходит путь l за время t, то v = l / t, a i =q / t. При этом оказывается, что на проводник с током, располо­женный в магнитном поле действует сила f₂, величина которой пропорциональна току i (или заряду q), а направление перпенди­кулярно оси проводника.

Существует определенное направление (обозначим его еди­ничным вектором n), такое, что если ось проводника оказывается перпендикулярной этому направлению, то сила f₂ будет макси­мальной по величине.

Заметим, что направление вектора оказывается совпадающим с направлением N магнитной стрелки в магнитном поле (рис. В.4). Это позволяет говорить об основной физической величине, характеризующей магнитное поле в данной точке – магнитной индукции В .

Рис.В.4

Магнитная индукция – это векторная величина, направление которой совпадает с направлением n. В общем случае сила f₂ определяется из соотношения f₂ = i[l,В] или f₂ = q[v, В], где [ , ] – знак векторного умножения.

Если направление проводника с током выбрано таким обра­зом, что сила f₂ оказывается максимальной по величине, то величина магнитной индукции находится как B=f₂ / i·l или B=f₂ / q·v. Определив, таким образом, направление вектора магнитной индукции в каждой точке магнитного поля, можно затем по­строить картину этого поля по линиям магнитной индукции. Ли­ниями магнитной индукции называются линии, касательные к которым в каждой их точке совпадают по направлению с векто­ром В. Эти линии на рис. В.5 снабжены стрелками, указывающи­ми направление вектора В. На рис. В. 5а изображены линии век­тора В линейного проводника с током, уходящим за плоскость чертежа (сравним их направление с направлением магнитной стрелки на рис. В.З).

Рис.В.5

Заметим, что вы­деление из электромаг­нитного поля двух сто­рон - электрического и магнитного поля - ока­зывается весьма удоб­ным по методическим соображениям. Кроме того, в инженерной практике встречаются ситуации, когда фактиче­ски проявляется только одна из этих сторон (как, например, в случае электростатического поля - см. выше). Но в общем случае эти две стороны связаны и проявляются совместно. Так на движущуюся в электрическом поле частицу с зарядом q и скоростью v действует сила Лоренца f=f₁+f₂= qE + q[v, В], одна из составляющих ко­торой f₁ обуславливается электрическим, а другая f₂ - магнитным полем. Отметим, что действие сил f₁ и f ₂ различно. Сила f₁ обу­словленная электрическим полем, может изменять как направление вектора скорости, так и его величину, а, следовательно, и кинетиче­скую энергию частицы. Сила f₂, обусловленная магнитным полем, направлена всегда перпендикулярно вектору скорости частицы и из­меняет только направление движения частицы.