9.4.Требования к частотным характеристикам несогласованных фильтров

Поскольку передаточная функция K(jω) любой электрической цепи с постоянными сосредоточенными параметрами — дробно-рациональная функция аргумента jω, то выражение квадрата ее модуля K² также будет дробно-рациональной функцией аргумента ω². Задача аппроксимации частотной характеристики фильтра нижних частот состоит в выборе такого вида этой функции, которая наиболее близка к характеристике идеального фильтра НЧ (см. рис. 92, а).

Обозначим искомую аппроксимирующую функцию H²(ω). Перейдем к безразмерной частоте, принимая за базисную частоту среза фильтра ω_c. Опуская индексы, обозначим безразмерную частоту ω. Задача аппроксимации АЧХ фильтра нижних частот сводится к поиску такой рациональной дроби H²(ω), у которой при 0 < ω < 1 отклонения от единицы не превосходят заданного малого значения, а при ω > 1 значение H²(ω) резко уменьшается с ростом частоты. Поставленным условиям удовлетворяет дробь вида H²(ω) = 1/[1 + έ²Q²_n(ω)], где Q_n(ω) — полином степени n, модуль которого в промежутке 0 < ω < 1 не превосходит единицы, монотонно возрастающий при ω > 1; έ — число, определяющее неравномерность характеристики в полосе пропускания. При нормировке соответствующего полинома с Q_{n max max} = 1 в полосе пропускания функция H заключена в пределах 1/√1+ έ²≤H ≤1. Поэтому величина έ связана с характеристикой неравномерности передачи фильтра в полосе пропускания Δα. Так как Δα = – 20 lg(1/√1+ έ²= 10 lg (1 + έ²), то соотношение, выражающее обратную зависимость, имеет вид έ = . Например, для заданной неравномерности в 3 дБ минимальное значение H_min в полосе пропускания равно 1/√2. Ему соответствует έ = 1.

В полосе задерживания значение H(ω) уменьшается тем быстрее, чем выше показатель степени полинома n. Заданная величина минимального ослабления в полосе задерживания α_min выражается через введенные функции: α_min = – 20 lg H(ω_з) = 10 lg [1 + έ²Q²_n(ω_з)], где ω_з — граничная частота полосы пропускания. При заданных α_min, έ, ω_з и семействе функций Q_n из последней связи можно определить степень n, обеспечивающую требуемый спад характеристики H(ω) в полосе задерживания.

Один из наиболее простых способов решения задачи аппроксимации состоит в выборе в качестве Q_n(ω) степенной функции ωⁿ. При этом выражение квадрата модуля H² принимает вид H² = 1/(1 + έ²ω²ⁿ). Эти зависимости монотонны во всем частотном диапазоне. Из рис. 9.12, на котором изображены кривые H²(ω) при n от 1 до 4, следует, что с ростом n  в полосе задерживания — при ω > 1 — значения H² уменьшаются, а  начальная часть кривых становится все более плоской — они приближаются к характеристике идеального ФНЧ. Рассматриваемый класс аппроксимации определяет фильтры с максимально плоскими характеристиками (фильтры Баттерворта).

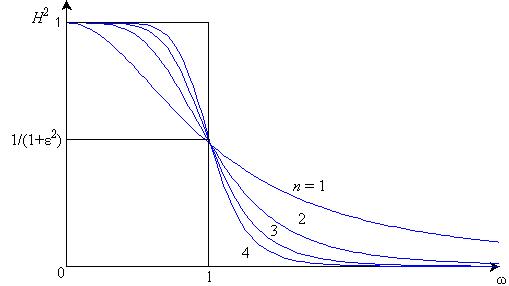
Рис. 9.12

Другой подход связан с использованием в качестве полиномов Q_n(ω) полиномов Чебышева T_n(ω) = cos(n arccos ω). Известно, что из всех полиномов n-й степени с одинаковыми старшими коэффициентами полином Чебышева наименее уклоняется от нуля на отрезке (– 1, 1), где он попеременно принимает максимальные и минимальные значения ± 1. Такое свойство полиномов Чебышева определяет равноколебательный характер функции

которая в полосе пропускания колеблется между значениями 1/(1 + έ²) и единицей. Число экстремумов функции в полосе пропускания  H² равно степени полинома n. С увеличением n спад частотной характеристики в полосе задерживания становится более резким, и характеристики этого класса также приближаются к характеристике идеального фильтра нижних частот (рис. 9.13).  Подобная аппроксимация носит название равноколебательной, а соответствующие фильтры называются фильтрами Чебышева.

Рис. 13.13

Сопоставим максимально плоские и равноколебательные характеристики, отвечающие одним и тем же значениям n и έ. При n = 3 и  = 1  = 1/(1 + ω⁶), а  = 1/[1 + (4ω³ – 3ω)²]. В полосе задерживания (ω > 1) вторая зависимость убывает быстрее. Например, при ω = 2 H_{м. п} = 0,124, а H_р.к = 0,038. Это соотношение носит общий характер: в полосе задерживания при данном n и любой частоте H_р.к < H_{м. п}.  Поскольку степень полинома n определяет число реактивных элементов в схеме фильтра, то заданное ослабление в полосе задерживания обеспечивается при равноколебательной аппроксимации более простой схемой с меньшим числом элементов, чем при максимально плоской.