9.2.Анализ идеального фильтра нижних частот при импульсном воздействии

Как мы установили, идеальный фильтр нижних частот должен иметь частотные характеристики, изображенные на рис.9.5, а его передаточная функция — описываться соотношениями:

Рис. 9.5

При подаче на вход такого фильтра сигнала f₁(t) со спектральной плотностью F₁(jω) на выходе будем иметь сигнал, Фурье-изображение которого равно F₂(jω) = K(jω)F₁(jω). Поэтому для выходного сигнала

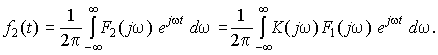
Первый сомножитель подынтегральной функции отличен от нуля лишь при – _c < ω < ω_c, и последний интеграл можно переписать в виде

При подаче на вход дельта-функции f₁(t) = δ(t) (рис.9.6, а), спектральная плотность которой равна F₁(jω) = 1, выходной сигнал выражается как

Рис. 9.6

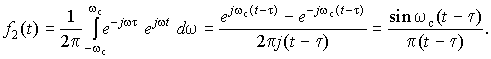
Таким образом, сигнал на выходе рассматриваемого идеального фильтра (рис. 9.6, б) должен был бы существовать и при t < 0, в то время как вызывающий его входной сигнал при t < 0 отсутствует. Иными словами, рассматриваемая идеальная цепь была бы способна вырабатывать выходной сигнал, прежде чем на ее вход подано вызывающее этот сигнал воздействие. Очевидно, никакая реальная физическая система подобным свойством, противоречащим принципу причинности, обладать не может. Отсюда следует, что построить фильтр с характеристиками, изображенными на рис. 9.5 — c постоянством передачи в полосе пропускания, нулевой передачей в полосе задерживания и скачкообразным переходом от одной полосы к другой  — принципиально невозможно. В связи с этим требования к амплитудно-частотной характеристике физически реализуемого фильтра, помимо сформулированных, должны включать также наличие полосы перехода — диапазона частот, разделяющего полосы пропускания и задерживания. В полосе перехода значения коэффициента передачи не нормируются, и происходит его плавное изменение от значений, требуемых в полосе пропускания до значений, допустимых в полосе задерживания.

9.3. Частотные свойства пассивного lc- фильтра нижних частот

Одна из простейших схем пассивного фильтра нижних частот, содержащая две индуктивности и емкость, приведена на рис. 9.7. Предположим, что нагрузкой фильтра нижних частот, представляющего  симметричный четырехполюсник с параметрами Z₁ = Z₃ = ; Z₂ = , является его характеристическое сопротивление Z_н = Z_c. 

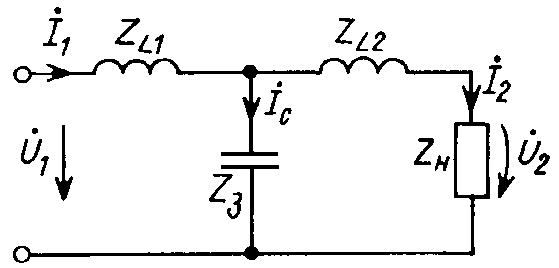
Рис. 9.7

Характеристические параметры такого четырехполюсника, определенные в п. 9.9, выражаются соотношениями:

 

или в безразмерной форме, с введением безразмерной частоты ω√LC/2 = ω_*:

Из последнего соотношения, используя формулу п. 9.9, найдем

Из этого выражения видно, что при ω_* < 1 или при ω < ω_c < 2/√LC мера передачи является чисто мнимой величиной Это неравенство определяет полосу пропускания фильтра, в которой затухание α = 0.

Характеристическое сопротивление, вещественное в полосе пропускания, уменьшается от значения Z_c0 = √L/C при ω = 0 до нуля на частоте среза ω_c. Это не позволяет обеспечить настройку фильтра в режим согласования во всей полосе пропускания: при нагрузке на постоянное сопротивление условие согласования можно выполнить лишь для одной фиксированной частоты.

В полосе задерживания характеристическое сопротивление имеет индуктивный характер. При этом схема рис. 9.7 состоит из одних реактивных элементов, и фазовый сдвиг между входным и выходным напряжениями равен 180°.

В полосе пропускания коэффициент фазы β = 2 arcsin ω_* и, следовательно, условие линейности фазочастотной характеристики фильтра не выполняется даже при согласованной нагрузке.

В полосе задерживания мера передачи имеет вещественную часть

.

Частотные зависимости α, β и Z_c изображены на рис. 9.8.

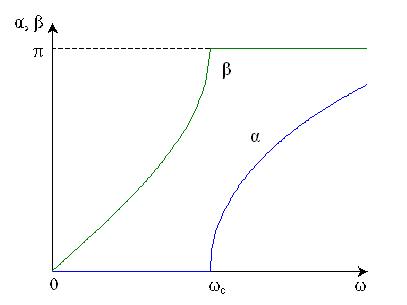
Рис. 9.8

Асимптотическое выражение для коэффициента затухания при ω→∞имеет вид α = 2 ln 2ω, или в децибелах — 20 * 2 lg 2ω= 20 lg 4 + 40 lg ω — асимптота логарифмической АЧХ фильтра имеет наклон 40 дБ/дек. Для практических применений такой характер роста затухания зачастую является слишком медленным. Более резкое возрастание коэффициента затухания в полосе задерживания получим при каскадном включении нескольких Т-образных звеньев. Трехзвенный фильтр (рис. 9.9) имеет асимптотический наклон ЛАХ в области высоких частот — (3* 40 = 120 дБ/дек). Однако и у него сохраняется невозможность согласования с резистивной нагрузкой в полосе пропускания.

Рис. 9.9

При постоянстве нагрузочного сопротивления фильтра Z_н = R₀ = const условие α = 0 = const в полосе пропускания не может быть соблюдено. Покажем это на примере однозвенного фильтра с параметрами Z₁ = Z₃ = jωL/2; Z₂ = 1/jωC, нагруженного на сопротивление Z_н = R₀. Воспользуемся выражением коэффициента передачи нагруженного четырехполюсника (см. п. 9.6) K_U = = Z_н/(A₁₁Z_н + A₁₂).

Используя связи между A- и Z-параметрами и соотношения для параметров Т-образной схемы (п. 9.2), получим

Поэтому ; = = = .

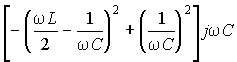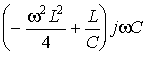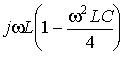Это дает для коэффициента передачи четырехполюсника, нагруженного на сопротивление R₀:

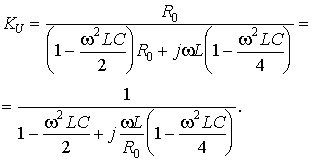
Приведем это выражение к безразмерным переменным, вновь принимая ω_* = ω√LC/2:

где ρ=√L/C /R₀.

Квадрат модуля знаменателя последнего выражения равен

Отсюда видно, что при любом постоянном значении ρ(или R₀) условие постоянства модуля коэффициента передачи фильтра в полосе пропускания обеспечить не удается.

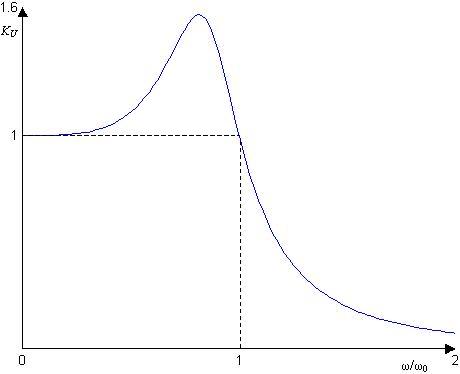
Рис. 9.10

Это иллюстрируется графиком рис.9.10 для ρ= 1 (или R₀ =√L/C), когда выражение модуля коэффициента передачи имеет вид

Таким образом, при формулировке реалистичных требований к частотным характеристикам фильтров (нагруженных на постоянное сопротивление, не зависящее от частоты) необходимо допустить изменения модуля коэффициента передачи фильтра в полосе пропускания (ПП) (ω_с1 < ω< ω_c2), не превышающие некоторого значения ΔK (рис. 9.11, а), задаваемого в качестве исходного при расчете фильтра, и плавный переход к полосе задерживания (ПЗ) (ω< ω_з1,ω> ω_з2), где значения коэффициента передачи не должны превышать некоторого заданного значения K_max.

a)

б)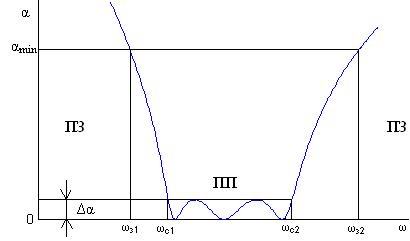

Рис. 9.11

Обычно эти характеристики задаются в децибелах — допустимая неравномерность коэффициента передачи в полосе пропускания характеризуется максимальным значением ослабления сигнала в полосе пропускания. Поскольку α = 20 lg U₁/U₂ = – 20 lg K_U, то α = – 20 lg (1 – ΔK). Аналогично, ослабление выходного сигнала в полосе задерживания не должно быть ниже α_min = – 20 lg K_max (рис. 9.11, б).