8.8. Уравнения и характеристические параметры симметричных четырехполюсников

Так как для симметричного четырехполюсника A₁₁ = A₂₂, то оба характеристических сопротивления становятся равными друг другу: Z_c11 = Z_c22 = Z_c = . Входное сопротивление симметричного четырехполюсника, нагруженного на характеристическое сопротивление Z_c, равно этому сопротивлению — сопротивление согласованной нагрузки как бы повторяется на входе четырехполюсника. Поэтому характеристическое сопротивление симметричного четырехполюсника называют также повторным.

Уравнения симметричного четырехполюсника принимают вид:

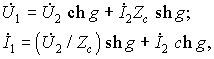
а выражения для коэффициентов K_U и K_I равны друг другу

и поэтому мера передачи симметричного четырехполюсника допускает наглядное истолкование

Вещественная часть меры передачи  — коэффициент затухания — определяет уменьшение действующих значений напряжения или тока при переходе от входных к выходным зажимам четырехполюсника при согласованной нагрузке. Мнимая часть  — коэффициент фазы — определяет изменение фазы тока и напряжения при переходе через согласованно нагруженный четырехполюсник  = ₁ – ₂. На практике затухание сигналов при переходе через четырехполюсник оценивается в децибелах и выражается через десятичные логарифмы:

Пример. Определим характеристические параметры симметричного четырехполюсника рис. 8.12, а.

Рис. 8.12

При холостом ходе сопротивления Z₁ и Z₀ в выходной цепи включены последовательно и оба параллельны сопротивлению Z₀ во входной цепи. Таким образом, для входного сопротивления имеем:

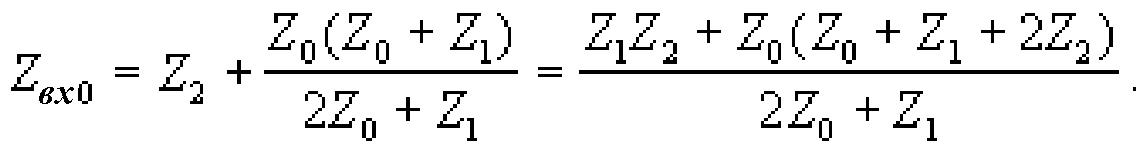
Аналогично при коротком замыкании на выходе сопротивления Z₂ и Z₀ выходной ветви соединены параллельно, а Z₀ входной ветви — последовательно с ними. Цепочка из указанных трех сопротивлений параллельна Z₁. В результате запишем

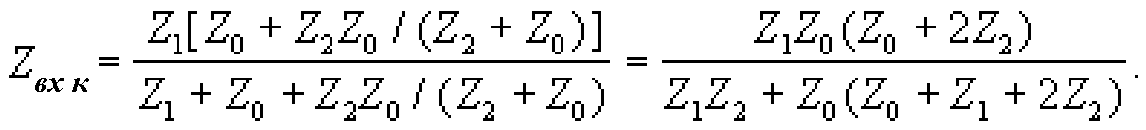
Используя оба выражения, определим характеристическое сопротивление цепи как

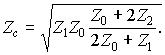
Если ее сопротивления связаны дополнительно условием: Z₁Z₂ = , то Z_c = Z₀, а g = ln .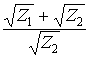

Для перехода к симметричной Т-образной схеме (рис. 8.12, б) в полученных соотношениях следует положить Z₁ = . Имеем:

или

откуда

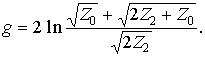
Для перехода к симметричной П-образной схеме (рис. 8.12, в) в общих выражениях следует принять Z₂ = 0. При этом:

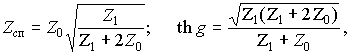или

откуда

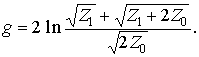
Еще один пример определения характеристических параметров симметричного четырехполюсника рассмотрен в Задаче 8.3.

8.9. Каскадное соединение согласованных четырехполюсников

Характеристические параметры легко позволяют вычислять коэффициенты передачи по напряжению и току цепочки каскадно соединенных согласованных четырехполюсников (см. рис.8.11), когда выполняются условия:

Z_c2(k) = Z_c1(k+1);  Z_г = Z_c11;  Z_c2n = Z_н. 

Поскольку коэффициенты передачи по напряжению каждого из четырехполюсников равны = , то при перемножении их коэффициентов передачи имеем

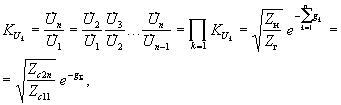
Аналогичный вид имеет и коэффициент передачи по току

Таким образом, при каскадном соединении мера передачи отдельных четырехполюсников суммируется: .

При каскадном соединении симметричных четырехполюсников полученные выражения упрощаются, так как у каждого из них Z_c2 = Z_c1:

Для каскада из n одинаковых симметричных звеньев с мерой передачи каждого g_k = g, имеем

A-параметры такого каскада равны: A₁₁ = A₂₂ = ch ng; A₁₂ = Z_c sh ng, A₂₁ = (1/Z_c) sh ng. Использование последних формул позволяет рассчитать токи и напряжения на входе и выходе каскада также и при отсутствии согласования на оконечных зажимах каскада. При этом сначала определяют характеристические параметры Z_c и g одного звена, затем по последним формулам находят A-параметры всего каскада, после чего используют уравнения в A-форме, позволяющие рассчитать режим при произвольных значениях Z_г и Z_н.

Пример. Рассмотрим однородную цепную LC-схему (рис. 8.13, а), которую можно представить как каскадное соединение n симметричных Т-образных звеньев (рис. 8.13, б).

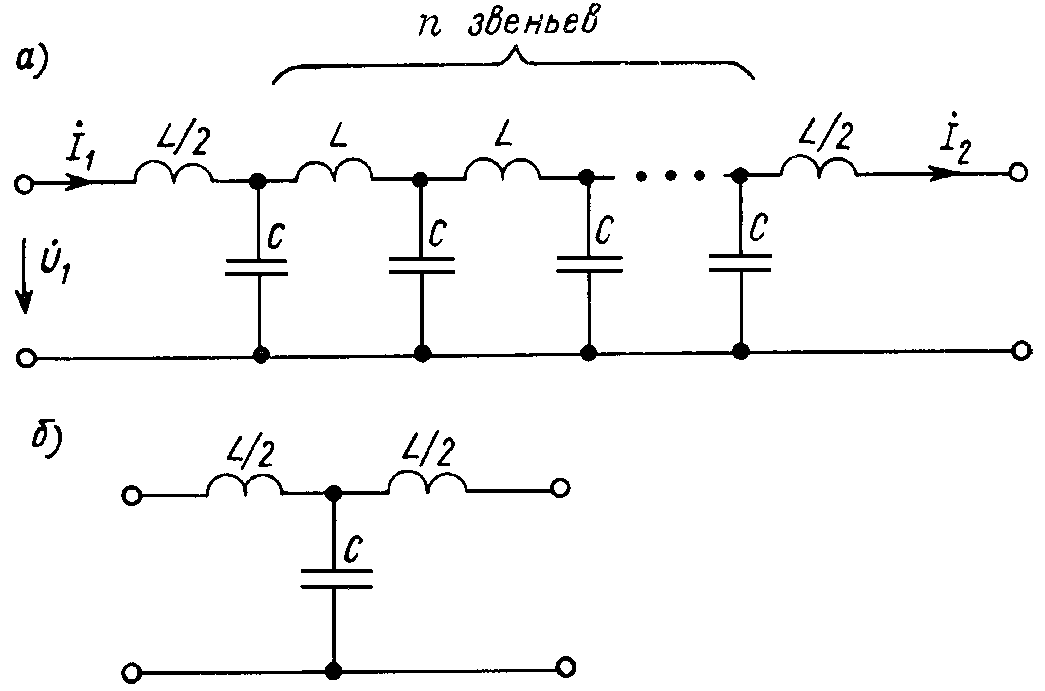
Рис. 8.13

Характеристические параметры одного звена найдем, используя соотношения для Т-звена, полученные выше (п. 8.8). Пωри Z₀ = jωL/2 и Z₂ = 1/jωC имеем:

В зависимости от соотношения между параметрами цепи и частотой рассматриваемая цепь обладает различными свойствами. При ω²LC/4 < 1 характеристическое сопротивление звена Z_cт вещественно, а g представляет чисто мнимую величину, так как модуль выражения под знаком логарифма равен единице. Поэтому в режиме характеристического согласования затухание сигнала в цепи отсутствует (α = 0), напряжения и токи в звеньях схемы, нагруженной на характеристическое сопротивление, изменяются лишь по фазе, а их амплитуды (действующие значения) сохраняются неизменными. Обозначая безразмерный параметр ω√LC/2 = ω_*, перепишем соотношение для меры передачи в этой области

Используя соотношение для мнимой части логарифма комплексного числа, найдем из последней связи:

Принимая ω_* = sin t, получим

поэтому окончательно для коэффициента фазы звена β будем иметь

Для каскадного соединения n одинаковых звеньев имеем соответственно коэффициент фазы nβ = 2n arcsin . Поэтому A-параметры каскада из n звеньев равны

При ω²LC/4 > 1, характеристическое сопротивление цепной схемы является, наоборот, чисто мнимым, а g имеет ненулевую вещественную часть — α ≠0. Поскольку g при этом имеет постоянную мнимую часть β = π, то фазовые сдвиги между напряжениями или токами на выходе отдельных каскадов в режиме согласования в этой области частот кратны π.

Пример расчета параметров каскадно соединенных согласованных четырехполюсников рассмотрен в Задаче 8.4.