8.6. Входные и передаточные функции нагруженных четырехполюсников

Рассмотрим связи между токами и напряжениями на входе и выходе четырехполюсника, питаемого от источника ЭДС с внутренним сопротивлением Z_г, к выходным зажимам которого подключено сопротивление нагрузки Z_н. При принятых направлениях выходных напряжения и тока (рис. 8.10, а) записывается в виде или .

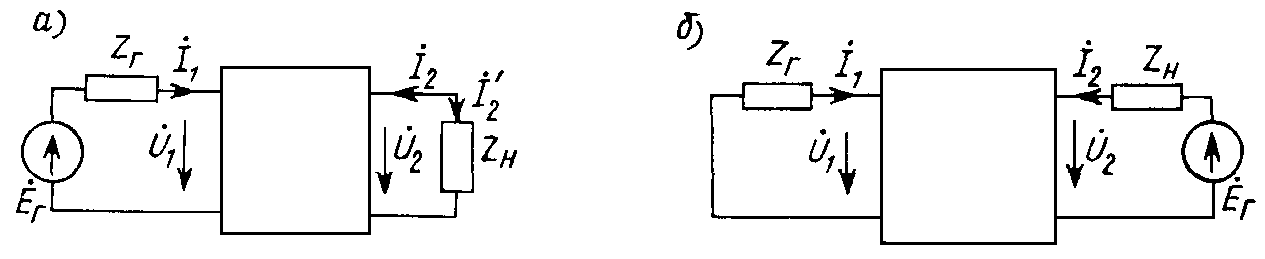
Рис. 8.10

Подставляя первое соотношение в A-уравнения четырехполюсника, выразим из них входное сопротивление нагруженного четырехполюсника как отношение входного напряжения к входному току

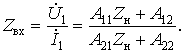
Для определения выходного сопротивления рассмотрим аналогичный режим, в котором источник ЭДС включен в выходную цепь, а входные зажимы четырехполюсника замкнуты на сопротивление Z_г (рис. 8.10, б). При этом, очевидно, . Использование этого выражения и A-уравнений четырехполюсника приводит к цепочке равенств

из которой найдем

Отсюда выходное сопротивление четырехполюсника выражается как отношение

Определим также соотношения для коэффициентов передачи по напряжению K_U и току K_I при питании четырехполюсника со стороны входа (см. рис. 8.10, а). Подставив соотношение между выходными величинами в A-уравнения четырехполюсника, получим из первого уравнения

откуда

Аналогично из второго уравнения четырехполюсника найдем коэффициент передачи по току

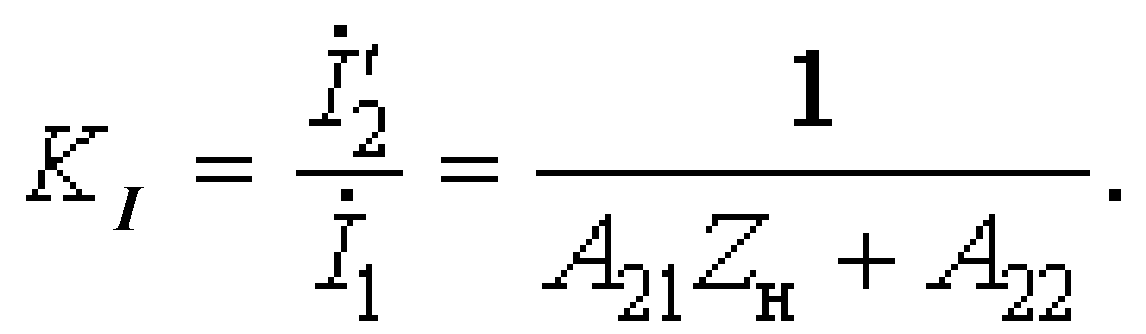
8.7. Характеристические параметры обратимых четырехполюсников

Введенные Z-, Y-, Н- и A-параметры четырехполюсника выражают соотношения между его входными и выходными токами и напряжениями независимо от режима нагрузки — значений сопротивлений Z_г и Z_н, включенных в его входной и выходной цепях (см. рис. 8.10). Часто каскадно соединенные элементы находятся в режиме согласованного включения, при котором выходное сопротивление каждого звена равно входному сопротивлению последующего. Так, четырехполюсник, изображенный на рис. 8.10, работает в режиме согласования на выходе, если его выходное сопротивление Z_вых равно сопротивлению нагрузки Z_н. Режим согласования будет обеспечен и на входе четырехполюсника, если его входное сопротивление Z_вх равно выходному сопротивлению генератора Z_г. Каскадно соединенные четырехполюсники (рис. 8.11) включены согласованно, если для каждой их пары выполняются условия: Z_{(k – 1) вых} = Z_k вх; Z_г = Z_1вх; Z_n вых = Z_н.

Рис.8.11

Рассчитать значения токов и напряжений в цепочке согласованно включенных четырехполюсников можно более простыми средствами, чем с помощью перемножения матриц их A-параметров.

Режим согласования на обеих парах зажимов четырехполюсника обеспечивается при вполне определенных значениях сопротивлений Z_г и Z_н, включенных в его входной и выходной цепях (см. рис. 8.10) и называемых характеристическими сопротивлениями четырехполюсника на входе и выходе (Z_c1 и Z_c2). Выразим их через A-параметры четырехполюсника. Согласование на входе имеет место при Z_г = Z_c1 = Z_вх, а на выходе — при Z_вых = Z_н = Z_c2. Используя выражения для входного и выходного сопротивлений нагруженного четырехполюсника (см. п. 8.6), запишем эти условия в виде:

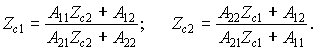
Приведем полученные соотношения к системе:

При вычитании и суммировании уравнений получим:

откуда Z_c1/Z_c2 = A₁₁/A₂₂ и Z_c1Z_c2 = A₁₂/A₂₁. Далее находим значения характеристических сопротивлений:

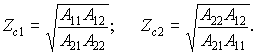
Полученные два параметра не дают полного описания обратимого четырехполюсника. Как мы установили ранее (см. п. 8.3), такой четырехполюсник характеризуется тремя независимыми параметрами. Для определения третьего из них рассмотрим коэффициенты передачи четырехполюсника по напряжению и току в режиме согласования. Преобразуем выражения для K_U и K_I с учетом того, что Z_н = Z_c2. Имеем

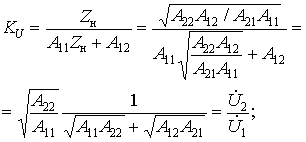
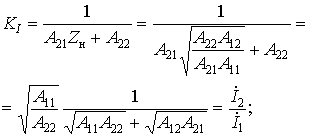
Здесь и далее положительное направление выходного тока принято в соответствии с рис. 8.11.

Третий характеристический параметр четырехполюсника — мера передачи g, связывает токи и напряжения на входе и выходе при условии согласования. Он определяется из соотношения

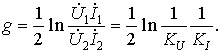
Используя выражения для K_U и K_I, получим

Выразим A-параметры четырехполюсника через Z_c1, Z_c2 и g. Из последнего выражения имеем . Обратная величина равна = . Здесь использована связь A₁₁A₂₂ – A₂₁A₁₂ = 1, справедливая для обратимого четырехполюсника.

Полусумма (e^g + e ^{– g})/2 = ch g = , а (e^g – e ^{– g})/2 = sh g = . Связи Z_c1/Z_c2 = A₁₁/A₂₂ и Z_c1Z_c2 = A₁₂/A₂₁ позволяют выразить A-параметры:

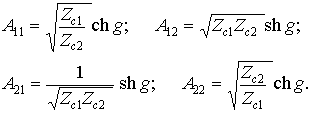
Запишем уравнения четырехполюсника с помощью характеристических параметров:

и коэффициенты передачи по напряжению и току в режиме характеристического согласования четырехполюсника:

Характеристические параметры позволяют также выразить его входные сопротивления Z₁₀ и Z_1к в режимах холостого хода и короткого замыкания на выходе. В первом случае = 0 и из системы уравнений получим Z₁₀ = = Z_c1/th g; при коротком замыкании = 0 и Z_1к = = Z_c1 th g. Из полученных связей имеем: Z_c1 = ; th g = . Меру передачи g выразим из последнего соотношения, используя тождество

Характеристическое сопротивление Z_c2 определяется аналогично Z_c1 через выходные сопротивления Z₂₀ и Z_2к в режимах холостого хода и короткого замыкания на входе четырехполюсника: