8.5. Определение параметров составных четырехполюсников. Каскадное, последовательное и параллельное соединение четырехполюсников

Рассмотрим сначала каскадное соединение, при  котором выходные ток и напряжение первого четырехполюсника являются входными для второго (рис. 8.7):

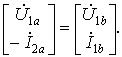
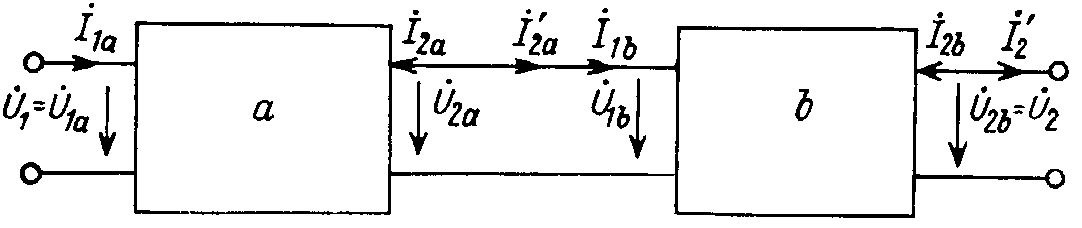
Рис. 8.7

Используя уравнения обоих четырехполюсников

получим для токов и напряжений на входе и выходе каскадного соединения:

Так как выходные величины составного четырехполюсника

то для каскадного соединения четырехполюсников a и b будем иметь

где

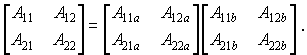
Таким образом, А-матрица составного четырехполюсника при каскадном соединении равна произведению А-матриц отдельных четырехполюсников. Так как произведение матриц в общем случае не обладает свойством коммутативности, то и A-параметры каскадного соединения двух четырехполюсников в общем случае зависят от последовательности их включения, так как A_aA_b  A_bA_a.

Из приведенных соотношений видно, что при рассмотрении каскадного соединения удобнее использовать другие направления выходных токов четырехпорлюсника, обозначенные на рис. 12.7 как İ '₂, İ '_2a.

При последовательном соединении четырехполюсников равны их входные и выходные токи (рис. 8.8, а): = = ; = = , а входное и выходное напряжения составного четырехполюсника равны сумме напряжений отдельных четырехполюсников ; .

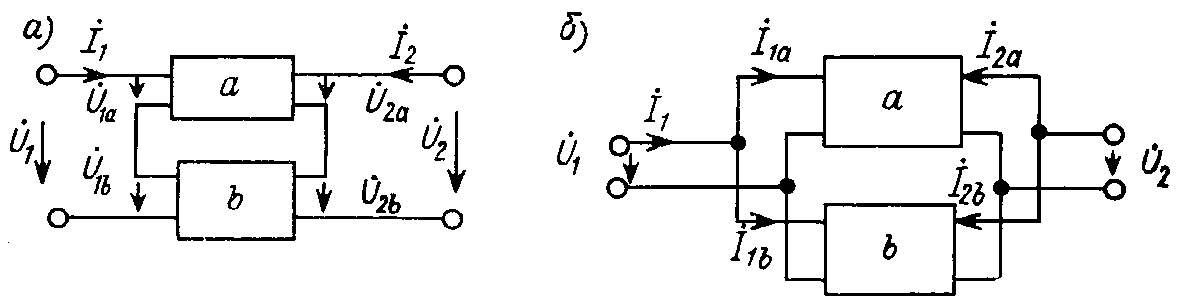
Рис. 8.8

Эти равенства проще всего использовать при описании четырехполюсников с помощью Z-параметров:

Суммируя напряжения и учитывая равенство токов, приходим к выводу, что Z-матрицы последовательно соединенных четырехполюсников суммируются

При параллельном соединении четырехполюсников (рис. 8.8, б) аналогично их входные и выходные напряжения одинаковы = = , = = , а суммируются токи — ; . Матрица параметров составного четырехполюсника в этом случае находится по Y-уравнениям:

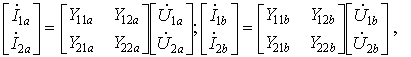
которые наиболее просто реализуют суммирование токов при параллельном соединении. Суммируя соответствующие уравнения обеих систем, придем к матричному равенству Y = Y_a + Y_b.

Определение параметров составных четырехполюсников при более сложных схемах соединений требует использования перечисленных правил и формул перехода от одной системы параметров к другой . В качестве примера рассмотрим схему трехполюсника, перекрытого ветвью с проводимостью Y и имеющего сопротивление Z в общей ветви (рис. 8.9).

Рис. 8.9

Ее можно рассматривать как последовательное соединение четырехполюсника a с общим зажимом (трехполюсника), имеющего матрицу параметров Z_a, с простейшим четырехполюсником b (см. рис. 8,5, а), параметры которого определялись ранее: . Суммирование Z-матриц Z_ab = Z_a + Z_b приводит к составному четырехполюснику ab (рис. 12.9). Теперь полученную схему можно рассматривать как параллельное соединение четырехполюсника ab и четырехполюсника c, состоящего из продольной проводимости Y (рис. 8.5, б). Используя его Y-параметры, найдем Y-параметры результирующего четырехполюсника, суммируя матрицы Y = Y_c + Y_ab. Для нахождения последней матрицы необходимо обратить матрицу Z_ab. Эту же задачу можно решать и иным путем, рассматривая сначала параллельное соединение четырехполюсника a и четырехполюсника c, представляемого проводимостью Y, с последующим суммированием Z-параметров полученного составного четырехполюсника и Z-параметров поперечного сопротивления Z. Разумеется, оба пути приводят к одинаковым значениям параметров составного четырехполюсника.

Пример определения параметров четырехполюсника при каскадном, последовательном и параллельном соединении составляющих его четырехполюсников рассмотрен в Задаче 8.2.