8.2. Эквивалентные схемы четырехполюсников

Эквивалентные схемы можно построить на основе уравнений четырехполюсника, записанных в Z-, Y- и H-формах. Поскольку четырехполюсник в общем случае описывается четырьмя независимыми параметрами, то каждая такая схема будет содержать четыре элемента. Так как Z-уравнения выражают напряжения на зажимах как сумму двух слагаемых, пропорциональных токам, то в схеме замещения имеем последовательное соединение сопротивлений и управляемых источников ЭДС (рис. 8.2, а).

Рис. 8.2

Аналогично Y-уравнения приводят к схеме рис. 8.2, б, реализующей принцип суммирования токов в параллельных ветвях, содержащих проводимости и управляемые источники тока. Подобным же образом строится схема замещения (рис. 8.2, в), отвечающая гибридным уравнениям.

На рис. 12.2, а-в изображены двухгенераторные эквивалентные схемы, каждая из них содержит два управляемых источника. На рис. 8.3, а, б показаны одногенераторные схемы, включающие лишь по одному управляемому источнику.

Рис. 8.3

Для входного и выходного напряжений Т-образной схемы рис. 8.3, а имеем:

Сопоставляя эти уравнения с Z-уравнениями четырехполюсника (8), получим условия их эквивалентности:

Z₁ + Z₂ = Z₁₁; Z₂ = Z₁₂;

Z₄ + Z₂ = Z₂₁; Z₃ + Z₂ = Z₂₂,

из которых найдем выражения для параметров Т-образной схемы через Z-параметры четырехполюсника:

Z₁ = Z₁₁ – Z₁₂; Z₂ = Z₁₂;

  Z₃ = Z₂₂ – Z₁₂; Z₄ = Z₂₁ – Z₁₂.

Аналогично параметры одногенераторной П-образной схемы (рис. 8.3, б) можно выразить через Y-параметры. Ее входной и выходной токи равны

; .

Эквивалентность этих уравнений Y-уравнениям четырехполюсника (8) обеспечивается при:

откуда получаем выражения для параметров П-образной схемы (рис. 8.3, б) через Y-параметры четырехполюсника:

8.3. Обратимые, симметричные и вырожденные четырехполюсники

Для обратимых четырехполюсников, в частности, для четырехполюсников, не содержащих управляемых источников, т. е. состоящих только из пассивных элементов, соотношения между входными и выходными величинами удовлетворяют принципу взаимности, откуда для них следуют равенства Z₁₂ = Z₂₁; Y₁₂ = Y₂₁. Поэтому обратимый четырехполюсник характеризуется лишь тремя независимыми параметрами. A-параметры обратимого четырехполюсника связаны соотношением _A = A₁₁A₂₂ – A₁₂A₂₁ = 1, справедливость которого можно проверить, используя связи между A- и Z-параметрами .

Анализируя соотношения для параметров одногенераторных схем замещения (см. рис. 8.3, а, б), приходим к выводу, что в рассматриваемых условиях Z₄ = 0; Y ₄ = 0, — схемы замещения обратимых четырехполюсников не содержат управляемых источников (рис. 8.4, а, б).

Рис. 8.4

Используя соотношения для Z-параметров одногенераторных схем (см. рис. 8.3), выразим параметры элементов Т-образной схемы (рис. 8.4, а) через Z-параметры четырехполюсника: Z₁ = Z₁₁ – Z₁₂; Z₂ = Z₁₂; Z₃ = Z₂₂ – Z₁₂.

Аналогично для параметров П-образной схемы (рис. 8.4, б) получим Y₁ = Y₁₁ + Y₁₂; Y₂ = – Y₁₂; Y₃ = Y₂₂ + Y₁₂.

Если параметры схем замещения требуется определить по другим системам параметров (H- или A-параметрам), то заданные их значения следует привести к Z- или Y-параметрам, используя соотношения между ними.

Симметричным называется четырехполюсник, у которого соотношения между токами и напряжениями не изменяются при перемене мест входных и выходных зажимов. Отсюда следует, что его Z- и Y-параметры не изменяются при взаимной замене индексов 1 и 2, т. е. Z₁₁ = Z₂₂; Z₁₂ = Z₂₁; Y₁₁ = Y₂₂; Y₁₂ = Y₂₁.

Вырожденным называется четырехполюсник, не имеющий каких-либо матриц параметров. Например, четырехполюсник, описываемый вырожденной матрицей Z, не имеет Y-параметров. Примером является четырехполюсник, составленный из одного сопротивления (рис. 8.5, а). Поскольку его входное и выходное напряжения одинаковы и равны , то . Очевидно, что определитель такой матрицы равен нулю, и обратная матрица Y не существует.

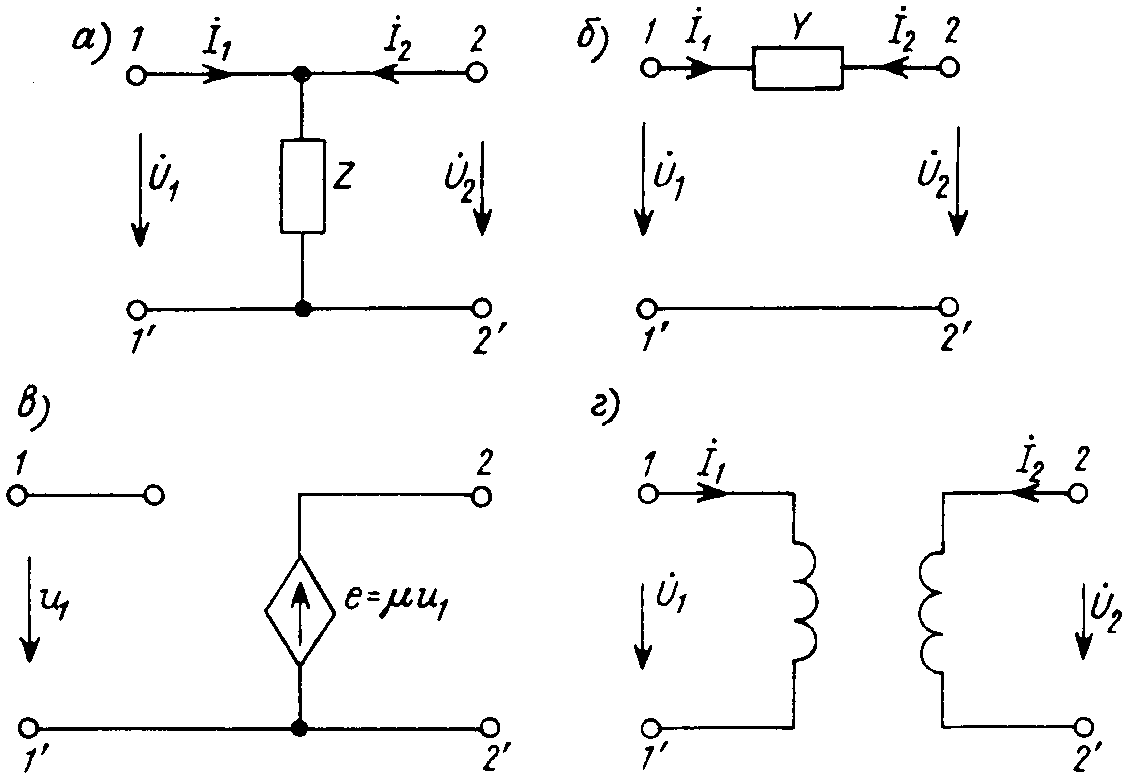
Рис. 8.5

Другой простейший четырехполюсник (рис. 8.5, б) описывается вырожденной Y-матрицей и не имеет Z-параметров.

Анализ выражений переходов к H-параметрам четырехполюсника (Приложение 1), приводит к заключению, что у четырехполюсника, у которого  Y₁₁ = 0, Z₂₂  = 0 или A₂₂ = 0, не имеет H-параметров. Этим свойством обладает любой четырехполюсник, имеющий разрыв во входной ветви или только идеальный источник ЭДС в выходной ветви. Таким свойством обладает, в частности, идеальный усилитель напряжения (рис. 8.5, в) 

Уравнения идеального трансформатора (рис. 8.5, г) и показывают, что его A-параметры определяются как A₁₁ = – c; A₁₂ = A₂₁ = 0; A₂₂ = – 1/c. Очевидно, он не имеет ни Z-, ни Y-параметров.