7.4. Зависимость формы кривой тока от характера цепи при несинусоидальном напряжении

Сопротивление электрической цепи, содержащей индуктивные катушки и конденсаторы, зависит от частоты и, следовательно, оказывается различным для разных гармоник. Поэтому если к зажимам такой цепи приложено периодическое несинусоидальное напряжение, то кривая тока в цепи отличается по форме от кривой напряжения.

Пусть в цепи, к которой приложено периодическое несинусоидальное напряжение, содержится только резистор R. Тогда

Сопротивление резистора не зависит от частоты. Поэтому процентное содержание высших гармоник в кривой тока такое же, как и в кривой напряжения следовательно, активное сопротивление не вносит искажений в форму кривой тока.

Пусть в цепи, к которой приложено периодическое несинусоидальное напряжение, содержится только индуктивная катушка с индуктивностью L. Тогда

где k= 2,3,4,… . Таким образом, содержание высших гармоник, выраженных в долях первой гармоники, в кривой тока меньше, чем в кривой напряжения. Говорят, что катушка сглаживает кривую тока.

Пусть в цепи, к которой приложено периодическое несинусоидальное напряжение, содержится только конденсатор емкостью С. Тогда

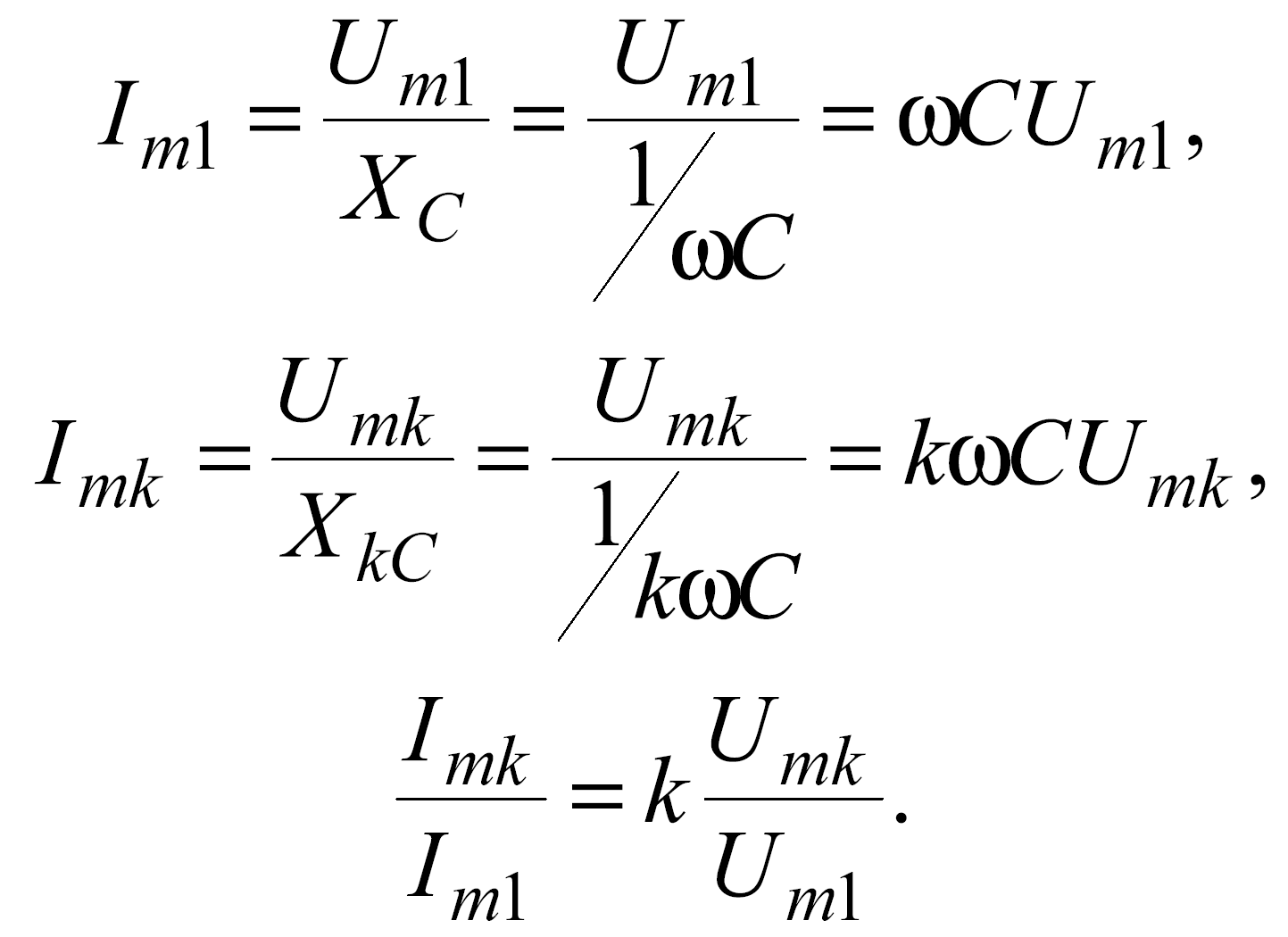
Содержание высших гармоник, выраженных в долях первой гармоники, в кривой тока больше, чем в кривой напряжения. Говорят, конденсатор искажает кривую тока по сравнению с кривой напряжения.

7.5. Действующее значение периодических несинусоидальных токов, напряжений, эдс

Для определения действующего значения любого периодического тока (напряжения, ЭДС) справедливо выражение 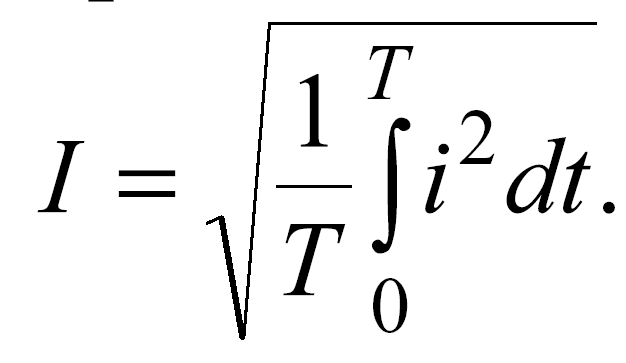В случае если ток представлен в виде ряда Фурье то







Если известны амплитудные значения функций, составляющих ряд Фурье, то действующее значение периодической несинусоидальной функции может быть найдено как

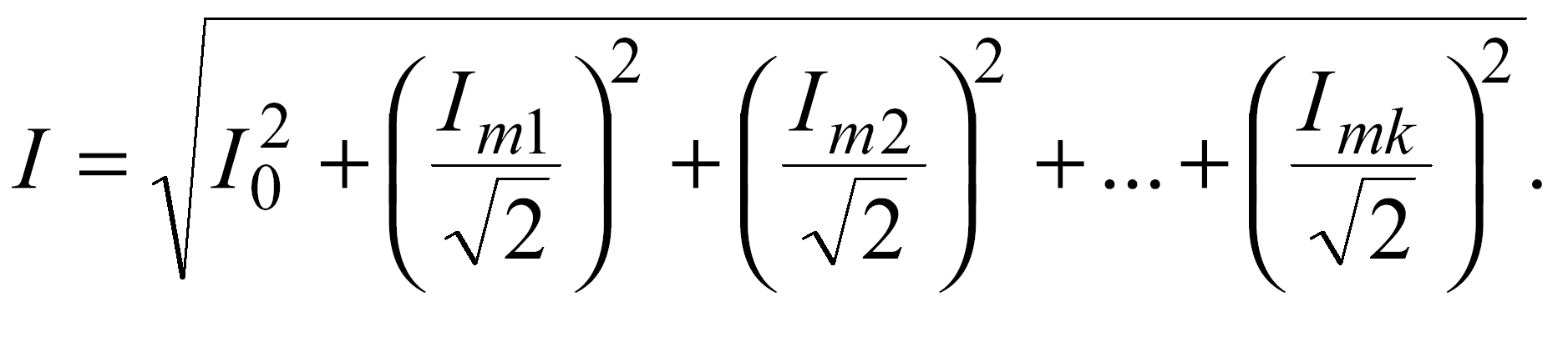
Аналогично для напряжения можно записать

7.6. Определение мощности в электрических цепях с периодическими несинусоидальными токами, напряжениями, эдс

Активная мощность при периодических несинусоидальных токах и напряжениях равна сумме активных мощностей постоянной и всех гармонических составляющих тока и напряжения

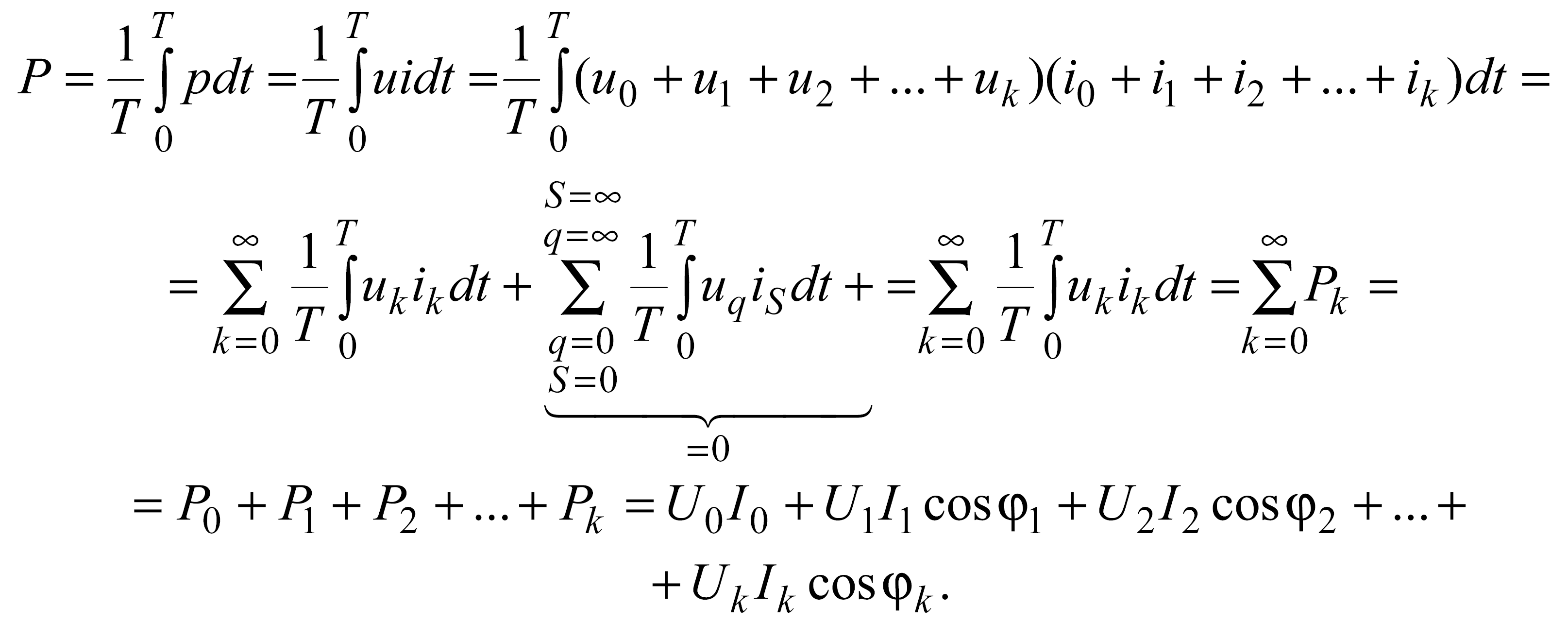
Коэффициент мощности при периодических несинусоидальных токах и напряжениях определяется из соотношения P = UI.

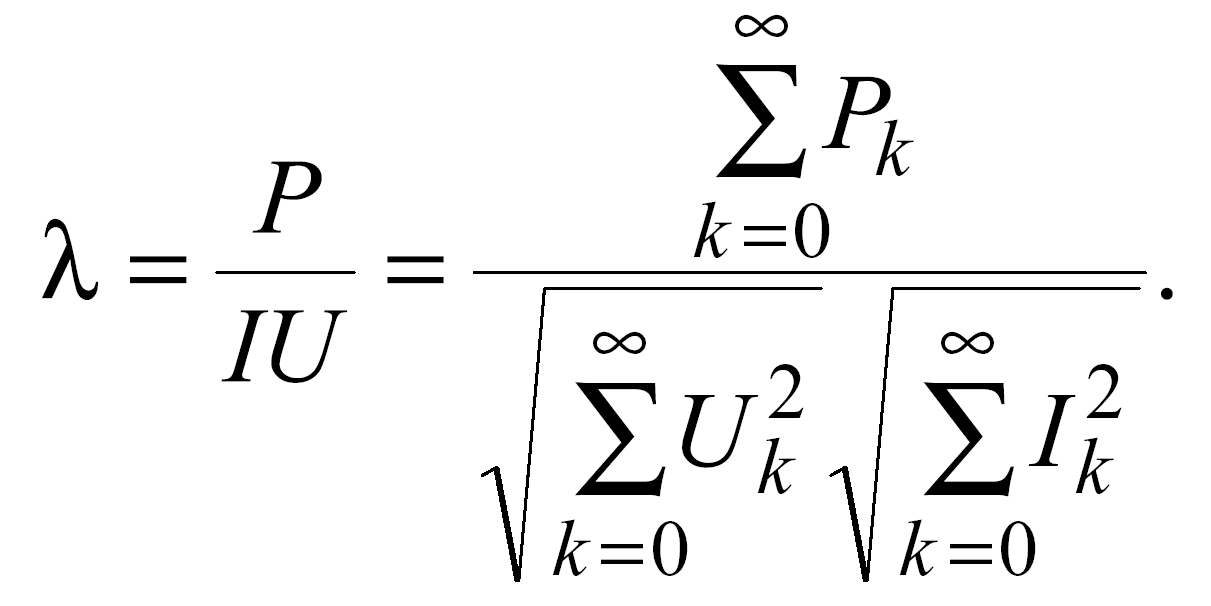
Величина =1 только в том случае, если цепь состоит только из активных сопротивлений, не зависящих от частоты. В случае, когда в цепи содержатся реактивные элементы, но отсутствуют постоянные составляющие и высшие гармоники, то = cos. Появление высших гармоник в кривых напряжения и тока ведет к снижению коэффициента мощности по сравнению со случаем, когда ток и напряжение при тех же действующих значениях синусоидальны.

Глава 8. Четырехполюсники. Частотные и временные характеристики

8.1. Основные уравнения четырехполюсников. Частотные характеристики. Фильтры

Четырехполюсник – это устройство, имеющее четыре контакта: два входных контакта используются для подключения источника сигнала и два выходных – для подключения нагрузки (рис. 8.1).

Рис. 8.1. Четырехполюсник: e_c(t) – ЭДС сигнала; Z_c – полное сопротивление

источника сигнала; u₁(t) – входное напряжение; i₁(t) – входной ток; u₂(t) – выходное

напряжение; i₂(t) - выходной ток; Z_н – полное сопротивление нагрузки

Четырехполюсники широко применяются в системах информации. Четырехполюсниками являются усилители, фильтры, линии связи и т.д.

Четырехполюсник, содержащий только линейные элементы, называется линейным.

Если внутри четырехполюсника есть нелинейные или параметрические элементы, то четырехполюсник будет нелинейным или параметрическим.

Четырехполюсник, не содержащий источников напряжения или тока, называется пассивным.

Активные четырехполюсники содержат источники напряжения или тока.

Теория четырехполюсников позволяет рассматривать устройство в виде «черного ящика», т.е. устройства с неизвестной для нас внутренней структурой. Свойства структуры будут проявляться через взаимосвязь входных и выходных токов и напряжений.

Рассмотрим уравнения линейных четырехполюсников.

Пусть заданы входной I₁ и выходной I₂ токи четырехполюсника (рис. 8.1). Входные и выходные напряжения U₁ и U₂ будут функциями этих токов:

; . (8.1)

Так как четырехполюсник линейный, то в силу принципа суперпозиции функции в уравнениях (8.1) будут линейными:

(8.2)

Коэффициенты Z₁₁, Z_12, Z_21, Z₂₂ имеют размерность сопротивлений. Соотношения (5.2) называют уравнениями четырехполюсника с Z-параметрами.

Если заданы напряжения четырехполюсника U₁ и U₂, то можно получить уравнения:

(83)

Коэффициенты Y₁₁, Y_12, Y_21, Y₂₂ имеют размерность проводимостей. Соотношение (8.3) называют уравнениями четырехполюсника с Y-параметрами.

При заданных I₁ и U₂ получаем уравнения с h-параметрами:

(8.4)

где h₁₁ = U₁/I₁, при U₂ = 0 – входное сопротивление при коротком замыкании на выходе;

h₁₂ = U₁/U₂, при I₁ = 0 – коэффициент обратной связи по напряжению;

h₂₁ = I₂/I₁, при U₂ = 0 – коэффициент прямой передачи по току;

h₂₂ = I₂/ U₂, при I₁ = 0 – выходная проводимость при холостом ходе на входе.

Название параметра указывает на способ его экспериментального определения или расчета.

Четырехполюсник в основном используются в системах передачи сигналов. Для анализа прохождения сигналов через четырехполюсник вводятся передаточные функции четырехполюсника.

– коэффициент передачи по напряжению;

– коэффициент передачи по току;

– коэффициент передачи активной мощности;

– полное входное сопротивление;

– полное выходное сопротивление.

Наиболее часто используемыми передаточными функциями являются коэффициент передачи по напряжению, входное и выходное сопротивление.

Если эквивалентная электрическая схема устройства неизвестна, то передаточные функции можно определить экспериментально по результатам измерений. После этого устройство можно использовать в качестве составной части других устройств.

Если эквивалентная электрическая схема устройства известна, то передаточные функции четырехполюсника можно рассчитать теоретически.

Четырехполюсник, коэффициент передачи которого зависит от частоты, называется электрическим частотным фильтром.

Пример 8.1. Найти выражения амплитудно-частотной и фазочастотной характеристик коэффициента передачи напряжения для четырехполюсника, изображенного на рис. 8.2, а.

Предположим, что сопротивление источника сигнала r_с много меньше входного сопротивления четырехполюсника , а сопротивление нагрузки R_н много больше выходного сопротивления четырехполюсника R. В этом случае можно пренебречь падением напряжения сигнала на сопротивлении источника, тогда , а также ответвлением тока в нагрузку, тогда .

Таким образом, коэффициент передачи напряжения .

В случае выполнения условий и , схему, приведенную на рисунке 8.2, а, можно упростить (рис. 8.2, б).

Учитывая, что ,

. (8.5)

Приводим (5.5) к каноническому виду:

;

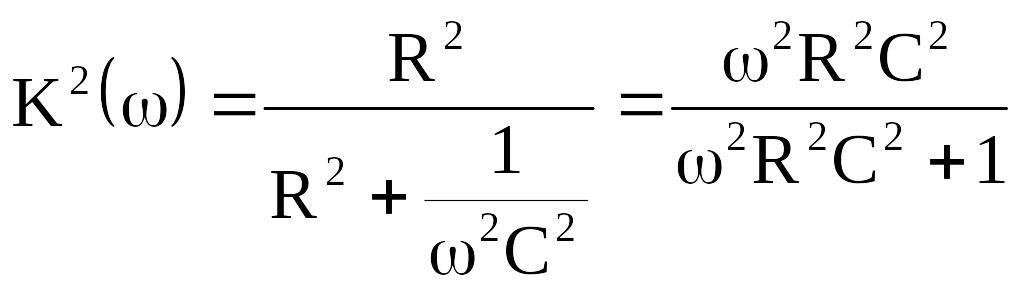. (8.6)

Подставляем в (5.6) характерные значения частот:

;

;

.

По полученным значениям строим АЧХ четырехполюсника (рис. 8.2, в).

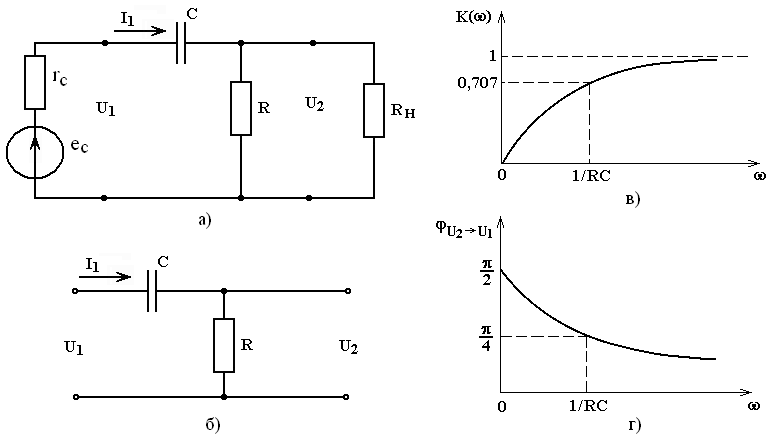
Рис. 8.2. RC-фильтр верхних частот первого порядка (а, б) и его АЧХ (в) и ФЧХ (г)

Сдвиг фаз между током I₁ и напряжением U₁ (см. § 4.2) составляет

. (8.7)

Поскольку выходное напряжение U₂ совпадает по фазе с током I₁, сдвиг фаз между выходным и входным напряжениями также можно определить по формуле (8.7).

Подставляем в (5.7) характерные значения частот:

;

;

.

По полученным значениям строим ФЧХ четырехполюсника (рис. 8.2, г).

АЧХ четырехполюсника (рис. 8.2, в) показывает, что сигнал начинает проходить через него с частоты . Частота называется частотой среза. Полоса частот выше частоты среза w_с называется полосой пропускания, а четырехполюсник, приведенный на рисунке 8.2, а, является фильтром верхних частот (ФВЧ). Количество независимых реактивных элементов определяет порядок фильтра.

Пример 8.2. Найти выражения амплитудно-частотной и фазочастотной характеристик коэффициента передачи напряжения для четырехполюсника, изображенного на рис. 5.3, а.

Рис. 8.3. RC-фильтр нижних частот первого порядка (а) и его АЧХ (б) и ФЧХ (в)

Коэффициент передачи напряжения

,

где – входное сопротивление четырехполюсника;

Х_С = 1/wС – выходное сопротивление четырехполюсника.

;

;

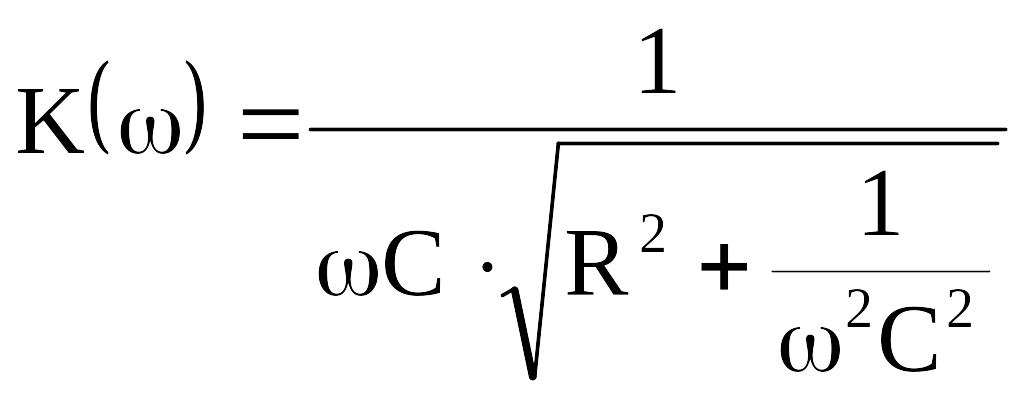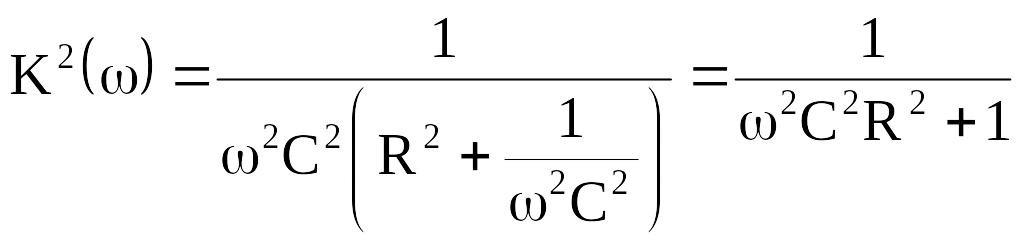. (8.8)

Подставляем в (8.8) характерные значения частот:

;

;

.

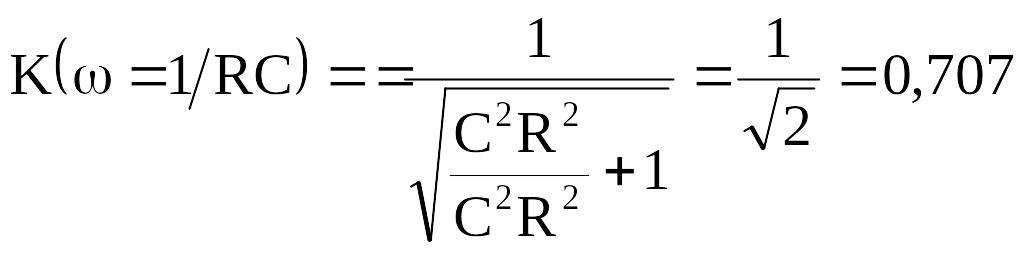По полученным значениям строим АЧХ четырехполюсника (рис. 8.3, б).

Сдвиг фаз между током I₁ и напряжением U₁ составляет

. (8.9)

Поскольку выходное напряжение U₂ совпадает по фазе с током I₁, сдвиг фаз между выходным и входным напряжениями также можно определить по формуле (8.9).

Подставляем в (5.9) характерные значения частот:

;

;

.

По полученным значениям строим ФЧХ четырехполюсника (рис. 8.3, в).

АЧХ четырехполюсника (рис. 8.3, б) показывает, что сигнал проходит через него, начиная с нуля до частоты среза . Поэтому четырехполюсник, приведенный на рисунке 8.3, а, является фильтром нижних частот (ФНЧ).

Пример 8.3. Найти выражение амплитудно-частотной характеристики коэффициента передачи четырехполюсника, изображенного на рис. 8.4, а.

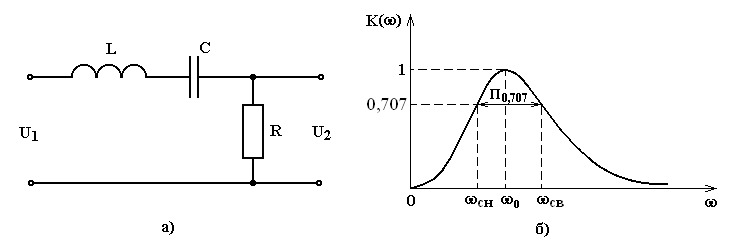
Рис.8.4. Полосовой RLC-фильтр второго порядка (а) и его АЧХ (б)

Коэффициент передачи напряжения

,

где – входное сопротивление четырехполюсника;

R – выходное сопротивление четырехполюсника.

;

;

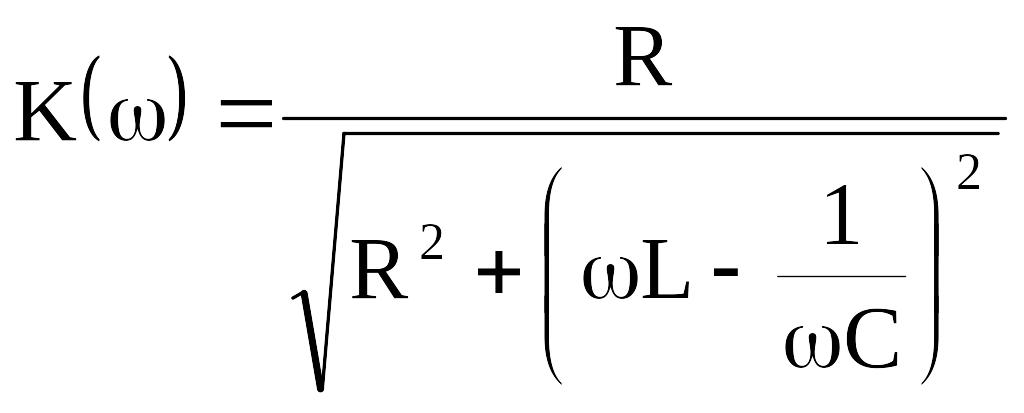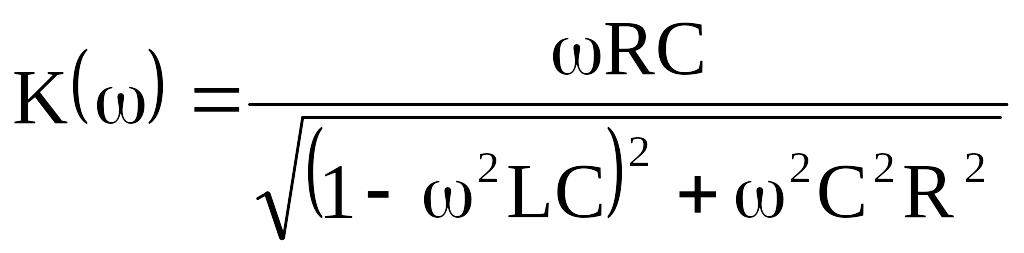. (8.10)

Подставляем в (8.10) характерные значения частот:

;

;

.

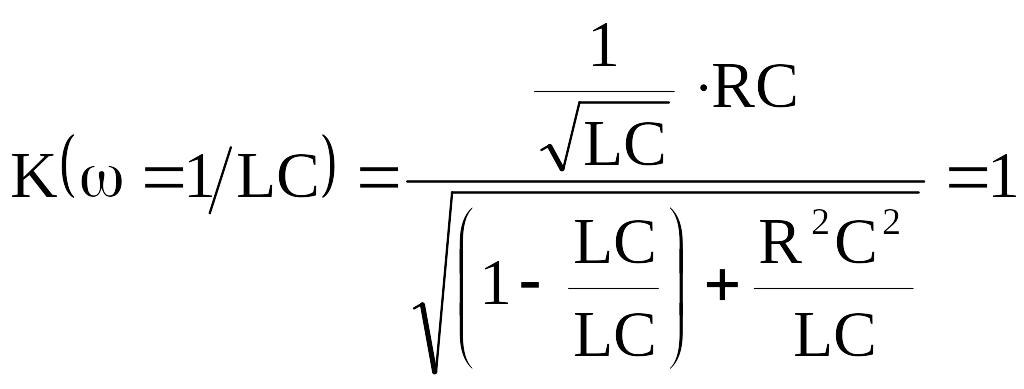По полученным значениям строим АЧХ четырехполюсника (рис. 8.4, б).

АЧХ четырехполюсника показывает, что сигнал проходит через него в полосе частот, геометрическим центром которой является резонансная частота w₀. Поэтому четырехполюсник, приведенный на рисунке 8.4, а, является полосовым фильтром (ПФ). Ширина полосы пропускания фильтра на уровне 0,707 от частоты w_сн до частоты w_св определяется по формуле:

,

где Q_к – добротность контура .

Пример 8.4. Найти выражение амплитудно-частотной характеристики четырехполюсника, изображенного на рис. 8.5, а.

Рис. 8.5. Режекторный RLC-фильтр второго порядка (а) и его АЧХ (б)

Коэффициент передачи напряжения

,

где – выходное сопротивление четырехполюсника;

– входное сопротивление четырехполюсника.

;

;

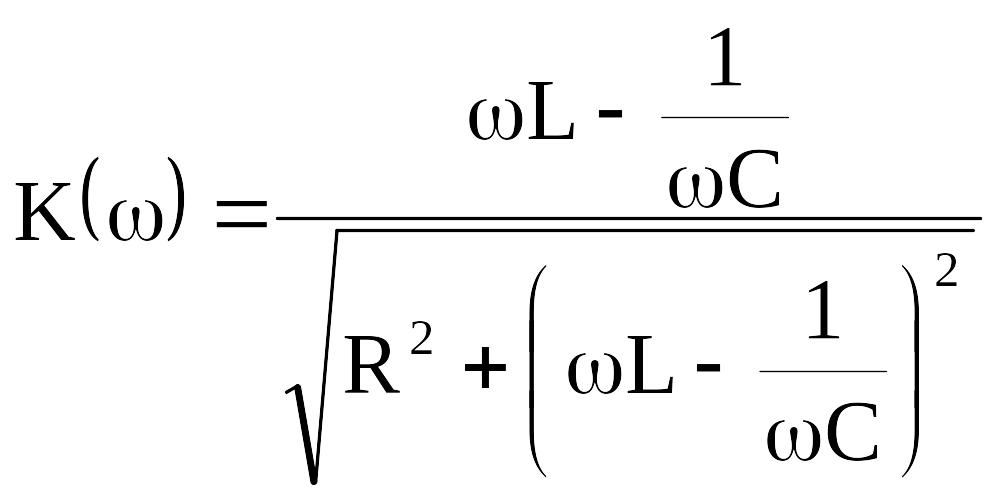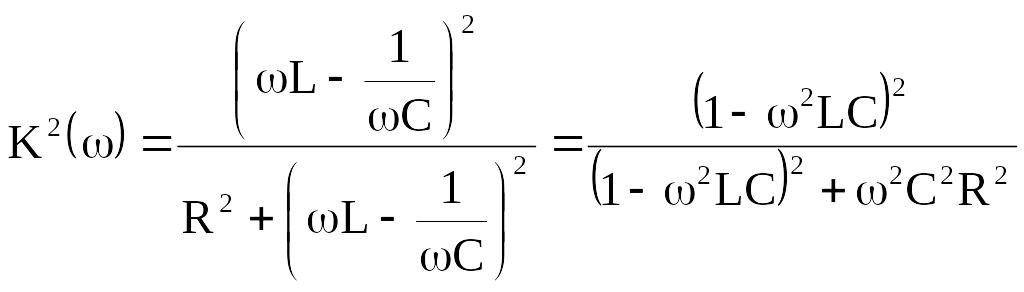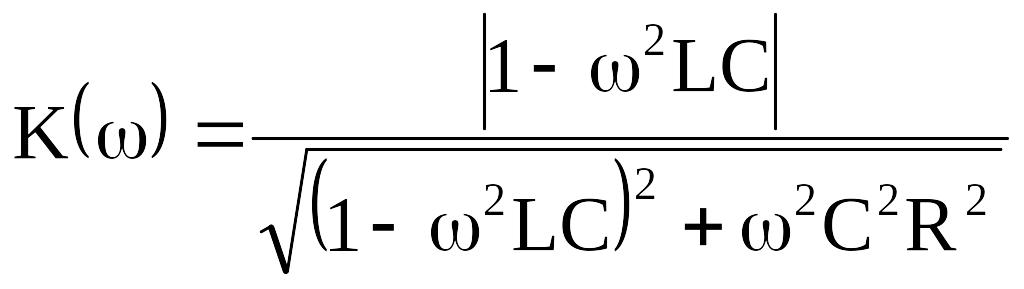. (8.11)

Подставляем в (8.11) характерные значения частот:

;

;

.

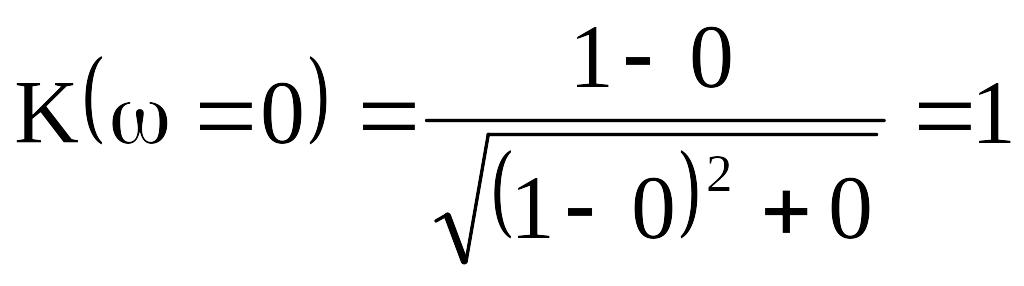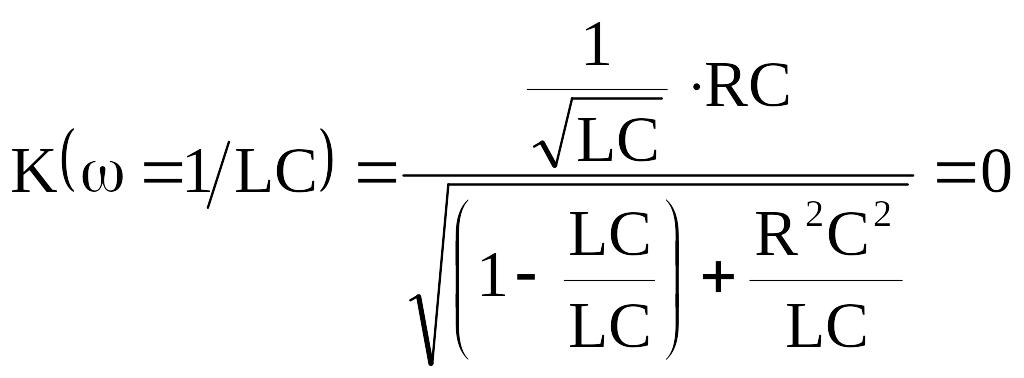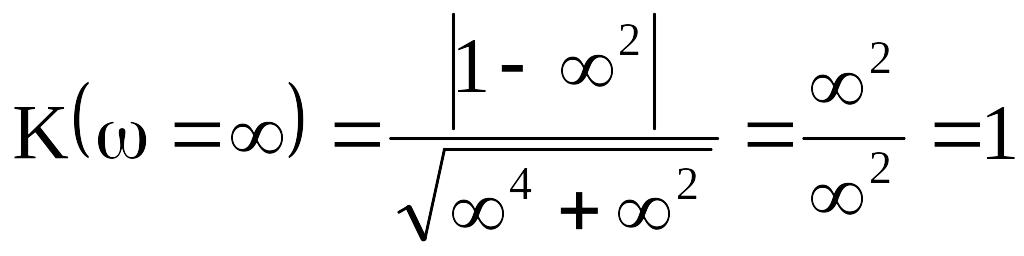По полученным значениям строим АЧХ четырехполюсника (рис. 8.5, б).

АЧХ четырехполюсника показывает, что сигнал проходит через него в полосах частот от нуля до частоты w_сн и от частоты w_св до бесконечности. В полосе частот, геометрическим центром которой является резонансная частота w₀, от w_зн до w_зв сигнал (помеха) подавляется. Поэтому четырехполюсник, приведенный на рисунке 5.5, а, является режекторным (заграждающим) фильтром РФ (ЗФ). Его назначение – подавить помеху (нежелательный сигнал). Ширина полосы заграждения определяется по формуле:

.

На функциональных схемах фильтры обозначаются в соответствии с рисунком 8.6.

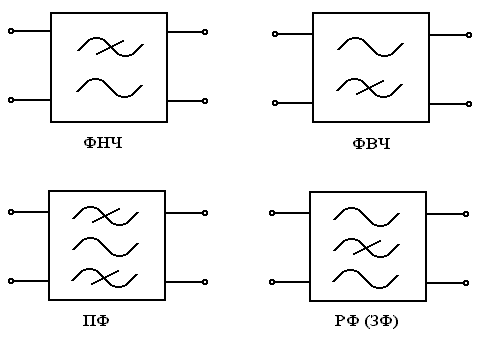
Рис. 8.6. УГО фильтров

Электрические частотные фильтры широко используются в системах передачи информации для выделения спектра полезного сигнала и подавления помех.

Расчетно-графическое задание № 3

Электрические фильтры

Задание: Произвести расчет режимов работы фильтра типа k по исходным

данным, указанным в табл.3.

Варианты задачи.

1. Фильтр верхних частот собран по Т-образной схеме. Ёмкость каждого

конденсатора С, индуктивность катушки L. На входные зажимы фильтра

подано напряжение U1 при частоте f. К выходным зажимам фильтра

подключено сопротивление Z_н, согласованное на заданной частоте с

характеристическим сопротивлением фильтра.

2. Фильтр верхних частот собран по П-образной схеме. Индуктивность каждой

катушки L , емкость конденсатора С. На входные зажимы фильтра подано

напряжение U1 при частоте f. К выходным зажимам фильтра подключено

сопротивление Z_н, согласованное на частоте f с характеристическим

сопротивлением фильтра.

3. Фильтр нижних частот собран по Т-образной схеме. Индуктивность каждой

катушки L , емкость конденсатора С. На входные зажимы фильтра подано

напряжение U1 при частоте f. К выходным зажимам фильтра подключено

сопротивление Z_н , согласованное на частоте f с характеристическим

сопротивлением фильтра.

4. Фильтр нижних частот собран по П-образной схеме. Ёмкость каждого

конденсатора С, индуктивность катушки L. На входные зажимы фильтра

подано напряжение U1 при частоте f. К выходным зажимам фильтра

подключено сопротивление Z_н, согласованное на заданной частоте с

характеристическим сопротивлением фильтра.

Вычислить характеристическое сопротивление фильтра Z_c и меру

передачи g = a + jb (a - собственное затухание, b - коэффициент фазы).

Используя Z_c и g , определить комплексы токов на входе и выходе фильтра.

Рассчитать все остальные токи и напряжения в схеме и построить полную

векторную диаграмму токов и напряжений.

Краткие теоретические сведения

Четырёхполюсник обладает свойствами фильтра только в том случае, когда

сопротивления Z₁ = ± j X₁ и Z₂ = ± j X₂ , входящие в Г - образные или

симметричные Т - и П - образные схемы (рис.47,48), имеют разные знаки.

Электрический фильтр наилучшим образом выполняет свои функции, если

он нагружен на сопротивление, равное характеристическому сопротивлению.

В теории фильтров, основанной на характеристических параметрах

четырёхполюсников, решаются следующие основные задачи:

1) устанавливаются условия, при которых фильтр имеет полосу

прозрачности;

2) определяется ширина полосы прозрачности;

3) находятся уравнения частотных характеристик (АЧХ и ФЧХ).

Для Г - образного звена - прототипа (рис.47) справедлива система

уравнений в параметрах прямой передачи:

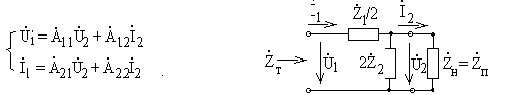
Рис.47

Определим А - параметры из режимов холостого хода и короткого

замыкания на выходе:

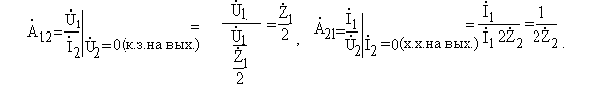
В теории четырёхполюсников показано, что характеристические

сопротивления (входные сопротивления в режиме двустороннего

согласования) определяются

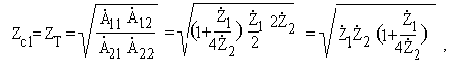
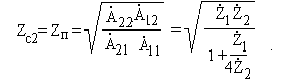
Постоянная передачи (мера передачи) g = a + jb может быть определена

из соотношения:

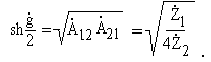
Т - и П - образные симметричные четырёхполюсники получаются

каскадным согласованным соединением двух Г-образных четырехполюсников

(рис.48), поэтому их постоянные передачи равны удвоенному значению

постоянной передачи Г- образного звена-прототипа.

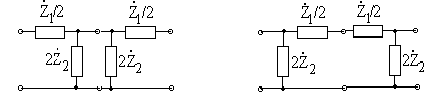
Рис.48

Для Т - и П - образных симметричных схем

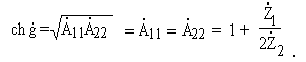
Характеристические сопротивления полученных звеньев остаются равными

соответствующим сопротивлениям Г - образного звена.

Так как фильтр нагружен на сопротивление, равное характеристическому,

соотношение напряжений и токов его на входе и выходе

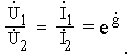
Из определения полосы прозрачности следует, что затухание а = 0;

фазовая же постоянная b в этой полосе частот может быть отличной от нуля.

Поэтому в полосе прозрачности g = a + jb оказывается мнимой величиной

и

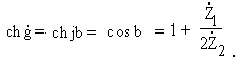
Поскольку cos b не может быть больше единицы, то необходимым условием

наличия полосы прозрачности является разный характер сопротивлений Z₁ и

Z₂ , т. е. если Z₁ = j X₁ положительно (имеет индуктивный характер), то Z₂

= - j X₂ должно быть отрицательным (ёмкостным) и наоборот. Это условие

необходимо, но не является достаточным.

cos b может изменяться в пределах от - 1 до + 1 , следовательно

Таким образом, для существования полосы пропускания необходимо и

достаточно, чтобы сопротивления X₁ и X₂ имели разные знаки, а по

абсолютной величине X₁ было бы меньше 4X₂: |X₁| < 4 |X₂| .

Граничные частоты полосы пропускания (частоты среза) можно определить

несколькими способами, используя основное неравенство теории фильтров

1. Если задан вид функций Z₁() и Z₂() , то граничные частоты

находятся из решения системы уравнений

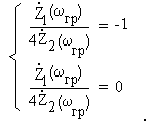
2. Если частотные зависимости Z₁() и Z₂() заданы графически, то

граничные частоты полосы пропускания могут быть также определены

графически (рис.49).

Рис.49

3. Граничные частоты могут быть найдены из рассмотрения зависимости

входного сопротивления фильтра, согласованного на выходе, т.е. с помощью

характеристического сопротивления:

При разных знаках Z₁() и Z₂() , а также при

произведение Z₁() на Z₂() действительное положительное число,

следовательно, характеристические сопротивления в полосе пропускания

являются действительными.

Поскольку характеристическое сопротивление четырёхполюсника является

средним геометрическим входных сопротивлений в режиме холостого хода -Z_x и

короткого замыкания -Z_к, то граничные частоты могут быть определены как

частоты, в пределах которых Z_x и Z_к имеют разные знаки (рис.50).

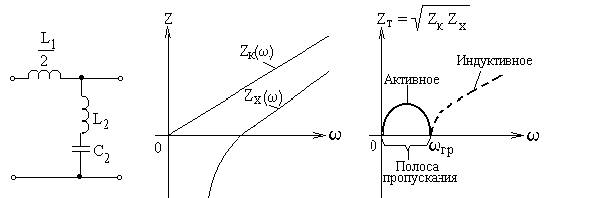
Рис.50

4. Выше было показано, что

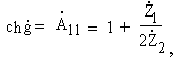
где

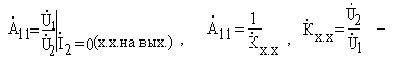
комплексный коэффициент передачи по напряжению в режиме холостого хода

на выходе.

В полосе пропускания

Из последнего выражения для модуля коэффициента передачи получим

Для граничных частот это неравенство обращается в равенство:

Таким образом, граничные частоты могут быть определены как частоты, на

которых коэффициент передачи при холостом ходе равен единице. Это

определение особенно удобно при экспериментальном исследовании фильтров.

Частотными характеристиками фильтра являются зависимости:

а() амплитудно-частотная характеристика,

b() фазо-частотная характеристика .

Для нахождения уравнений частотных характеристик используем выражение

для постоянной передачи Г - образного звена

Разделив вещественную и мнимую части, получим

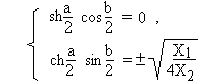
В полосе пропускания а = 0 следовательно 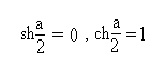, и

Поскольку сопротивления Х₁ и Х₂ зависят от частоты, то из

последнего уравнения получим зависимость коэффициента фазы от частоты в

полосе пропускания (ФЧХ) в виде

Амплитудно-частотная характеристика в полосе пропускания а() = 0

сливается с осью частот.

В полосе подавления следовательно,

отсюда b=± и а значит

Уравнение амплитудно-частотной характеристики в полосе подавления

Фазо-частотная характеристика в полосе подавления b()=±

Пример 1. Для схемы П- образного ФНЧ (рис.51), согласованного с

нагрузкой, рассчитать токи во всех ветвях и напряжения на элементах при

заданном входном напряжении. Построить векторные диаграммы рассчитанных

токов и напряжений.

Рис.51

Решение. Для П - образного фильтра нижних частот

,

значит фильтр работает в полосе пропускания и затухание а = 0.

Характеристическое сопротивление

Коэффициент фазы

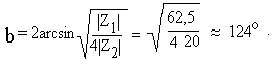
Рассчитаем граничную частоту фильтра

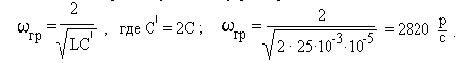
(Заданная по условию частота находится в полосе пропускания фильтра).

Выходное напряжение

Напряжение на индуктивности

Токи в ветвях

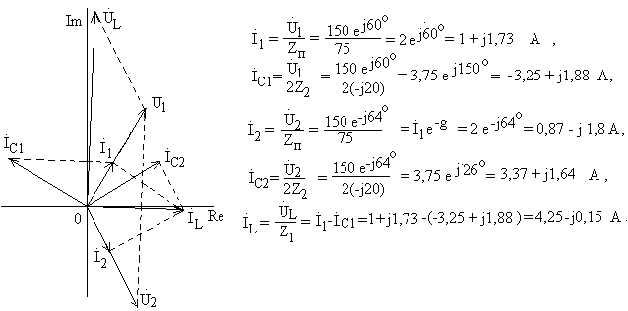
Рис.52

Векторная диаграмма токов и напряжений , построенная по результатам

расчетов, приведена на рис.52.

Пример 2. Изменим в предыдущем примере частоту так, чтобы получить

полосу подавления, например = 4000 р/c.

Тогда

значит фильтр работает в полосе подавления и

Характеристическое сопротивление

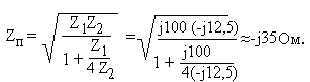
Затухание

Выходное напряжение

Напряжение на индуктивности

Токи в ветвях

Рис.53

Векторная диаграмма токов и напряжений в полосе подавления приведена

на рис.53.