5.2. Расчет последовательного соединения двух магнитосвязанных катушек

В случае последовательного соединения двух магнитосвязанных катушек возможно два вида включения: одноименными зажимами и разноименными зажимами, как это представлено, соответственно, на рис. 5.2 и рис. 5.3.

Рис. 5.2

Рис. 5.3

Пользуясь правилом определения знака перед напряжением, обусловленным взаимной индукцией, запишем уравнения по второму

закону Кирхгофа для случая включения катушек одноиме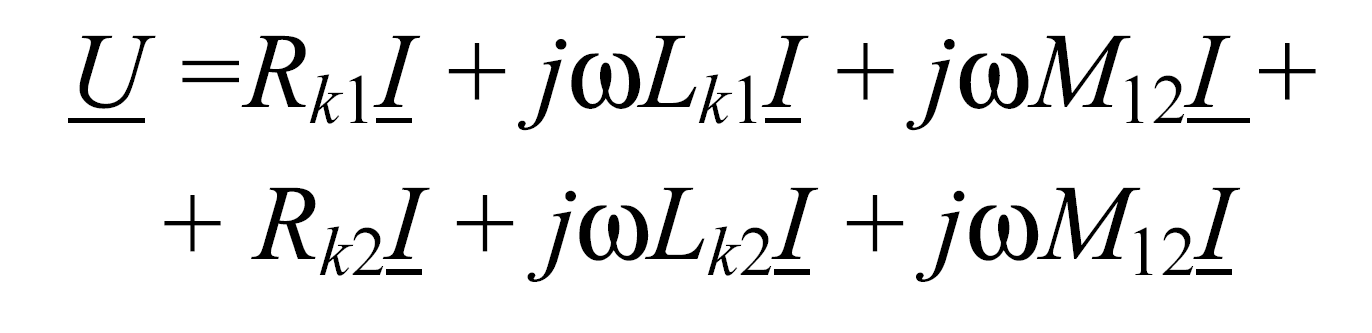нными зажимами

и для случая включения катушек разноименными зажимами

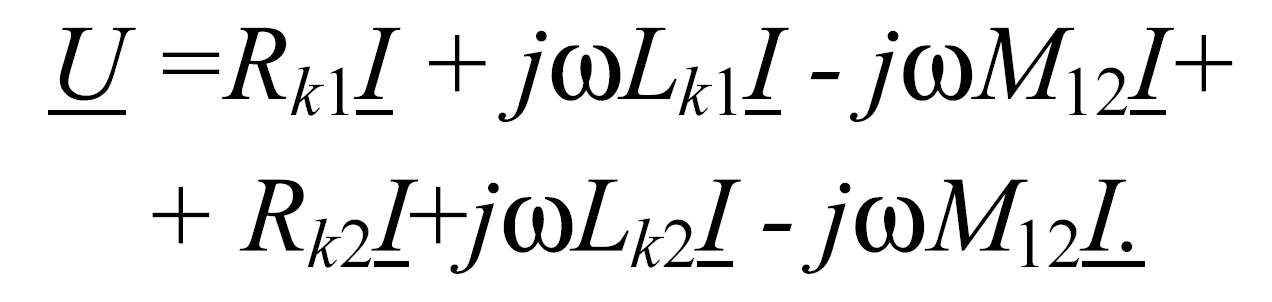После упрощения эти уравнения принимают вид:

или

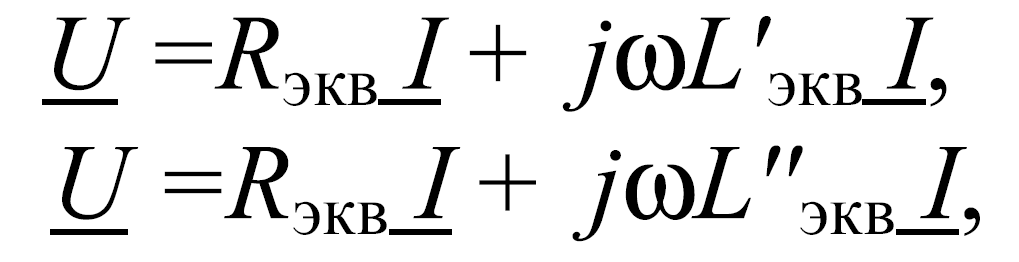
где Rэкв=Rk1+Rk2 – эквивалентное активное сопротивление; L'экв=Lk1+Lk2+2М – эквивалентная индуктивность одноименного включения катушек; L''экв=Lk1+Lk2–2М – эквивалентная индуктивность разноименного включения катушек. Зная величины L'экв и L''экв, можно определить коэффициент взаимной индуктивности М:

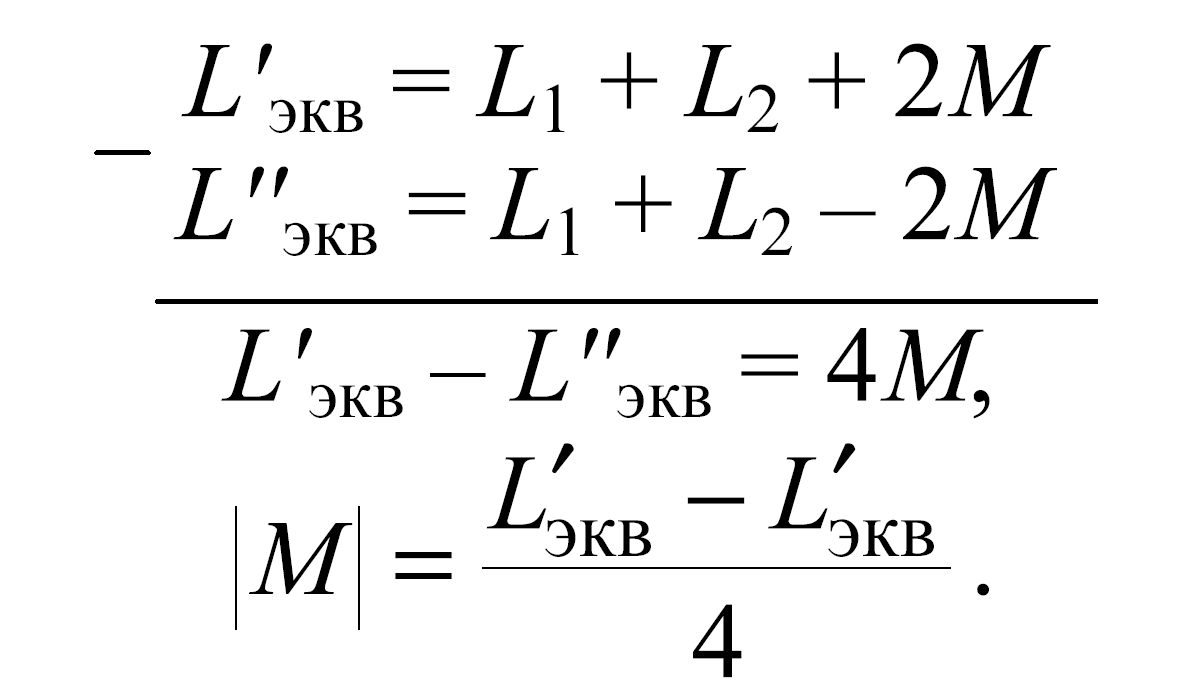
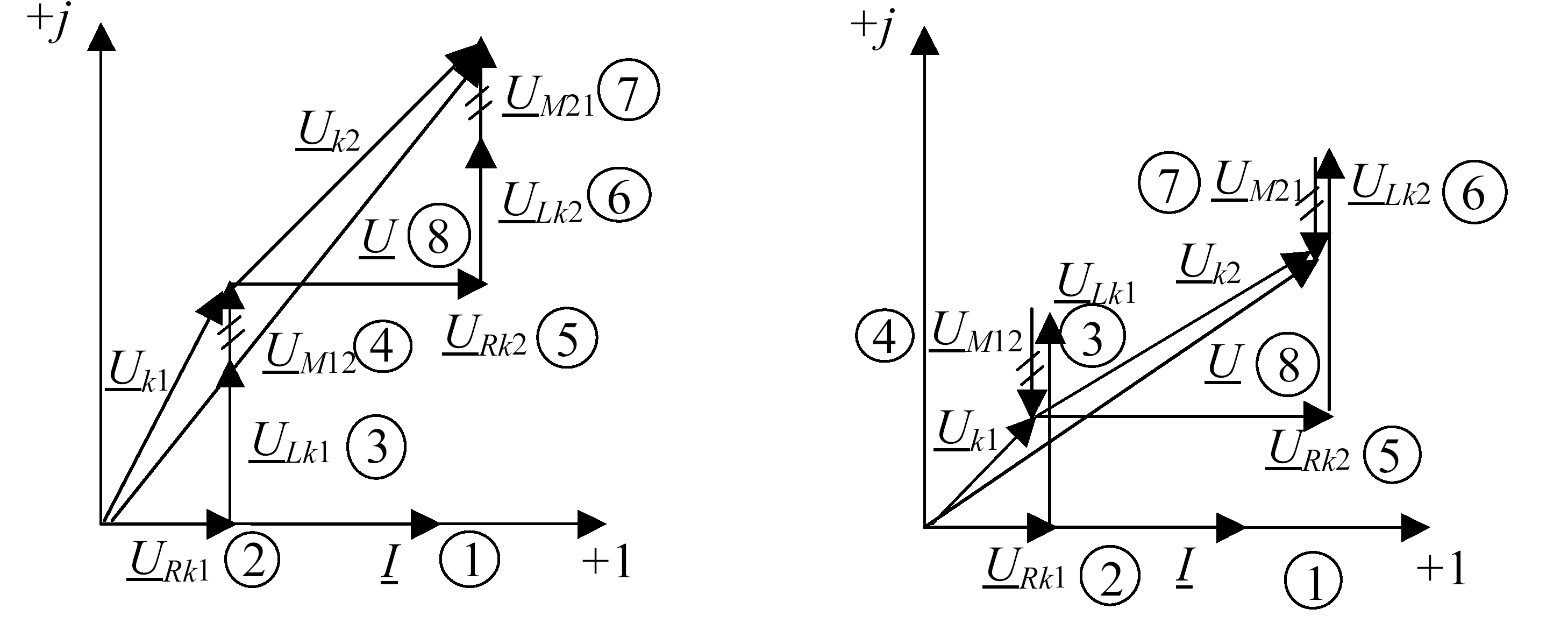
Рис. 5.4

Векторные диаграммы (рис. 5.4) для одноименного и разноименного включения катушек построены для одинакового значения тока в обоих случаях.

5.3. Расчет разветвленных цепей при наличии в них магнитосвязанных катушек

Задача расчета разветвленных электрических цепей при наличии в них магнитосвязанных катушек решается однозначно, если известны маркировка катушек и величина коэффициента взаимной индуктивности. Для расчета цепей применимы методы формирования уравнений по законам Кирхгофа и метод контурных токов, а также метод эквивалентного генератора, если отсутствует индуктивная связь между двухполюсником и выделенной ветвью. Нельзя применять без проведения специальных преобразований метод узловых потенциалов, формулы эквивалентного преобразования соединения треугольником в эквивалентное соединение звездой и обратно. Применение этих методов и формул требует введения дополнительных правил.

Запишем уравнения по законам Кирхгофа для цепи с магнитосвязанными катушками.

Пусть имеется электрическая схема (рис. 5.5), в которой присутствуют магнитосвязанные катушки.

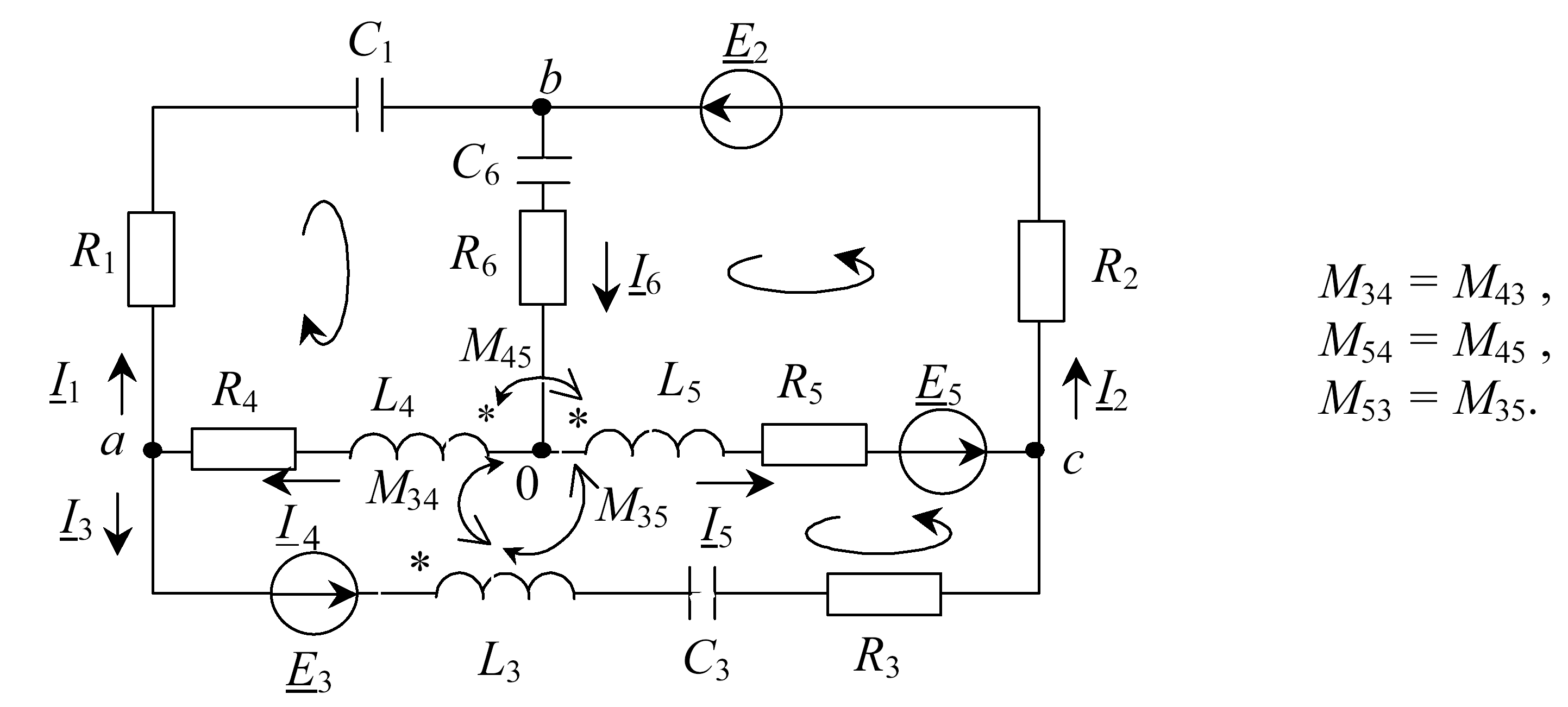
Рис. 5.5

По первому закону Кирхгофа запишем уравнения для узлов a, b, c.

Узел а i4 - i1 – i3 = 0 ,

узел b i2 + i1 – i6 = 0 ,

узел с i3 + i5 – i2 = 0.

Три уравнения по второму закону Кирхгофа запишем, считая, что конденсаторы не обладали начальным зарядом:

Эти же уравнения в комплексной форме могут быть записаны как

Знак напряжения, обусловленного взаимной индукцией, определяется по приведенному выше правилу. Учет взаимной индукции в случае составления уравнений по методу контурных токов осуществляется в виде введения дополнительных членов в выражения для собственных и взаимных сопротивлений контуров. При этом общий вид системы уравнений остается без изменений. Так, для приведенной выше схемы необходимо записать систему из трех уравнений:

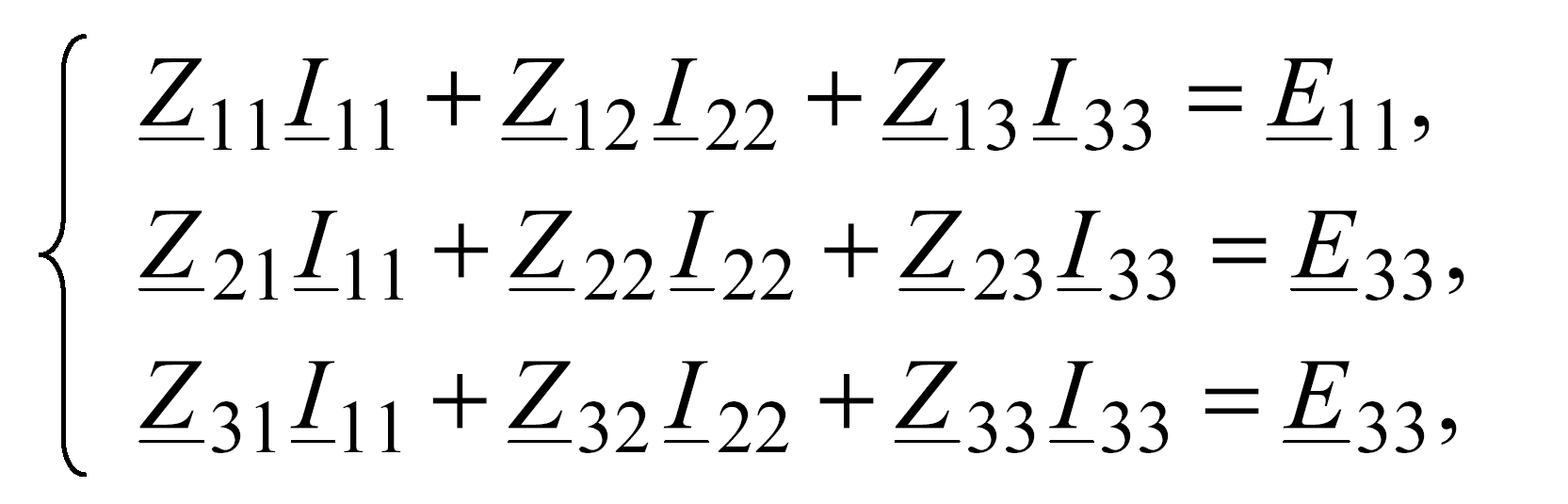
где, например

а – сопротивления, обусловленные явлением взаимной индукции, причем их знак определяется аналогично приведенному выше правилу.

5.4. «Развязывание» магнитосвязанных цепей

Невозможность непосредственного использования эффективных методов расчета, таких как, например, метода узловых потенциалов, приводит к необходимости осуществления так называемой развязки магнитосвязанных цепей.

Суть: исходную схему с магнитосвязанными индуктивностями путем введения дополнительных индуктивностей и изменения имеющихся преобразуют так, чтобы устранить магнитную связь между индуктивностями.

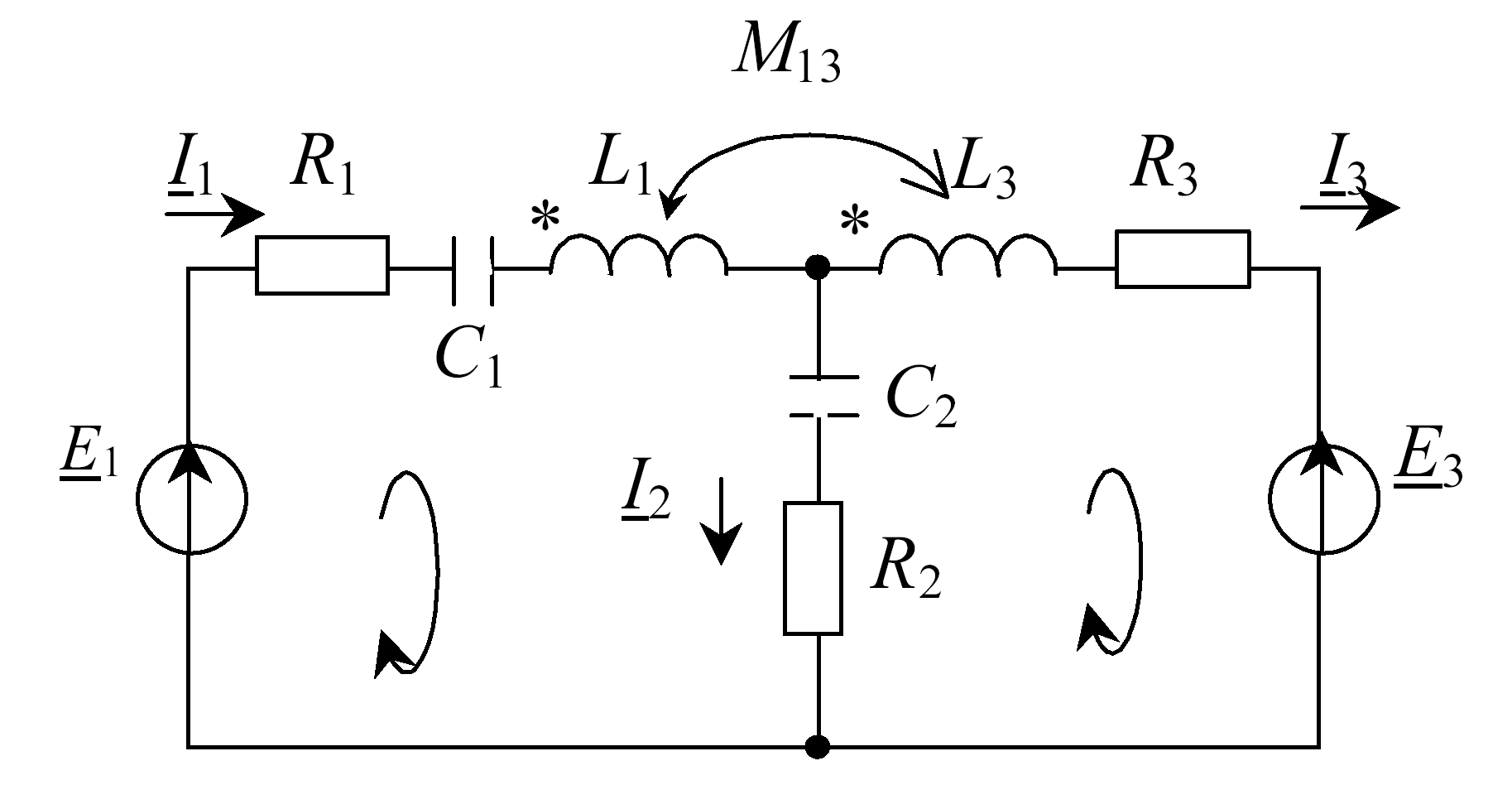
Рис. 5.6

Преобразования осуществляют на основе составленных по законам Кирхгофа уравнений для исходной схемы. Вновь полученная и исходная схема в расчетном смысле должны быть полностью эквивалентны.

Составим уравнения по законам Кирхгофа для схемы, приведенной на рис. 5.6

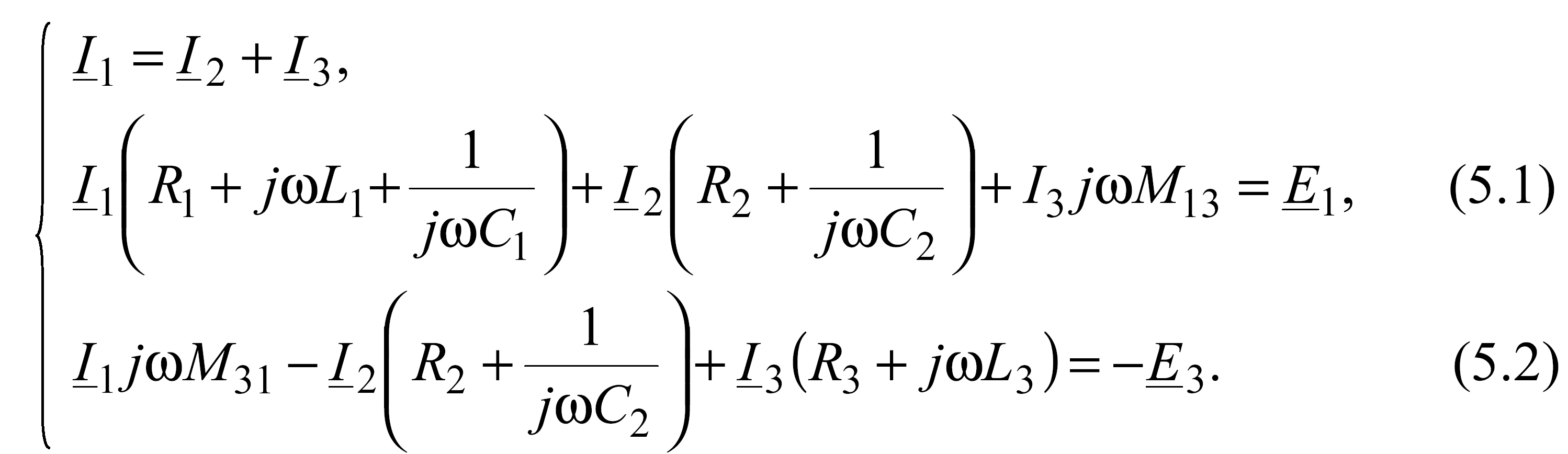
Подставив в уравнение (5.1) а в уравнение (5.2) запишем:

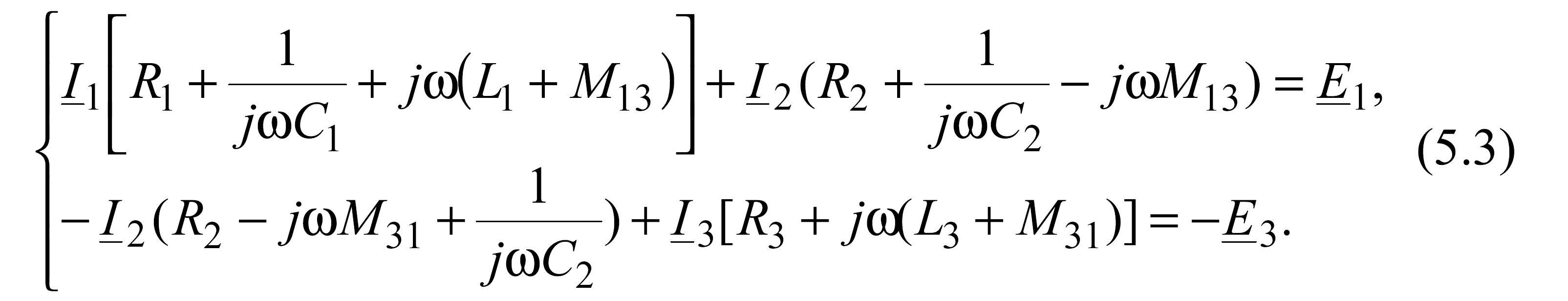
Полученная система уравнений (5.3) позволяет построить схему электрической цепи (рис. 5.7), в которой магнитосвязанные индуктивности L1 и L3 заменены соответственно индуктивностями (L1+М) и (L3+М) и, кроме того, введена дополнительная индуктивность L2=- М.

Рис. 5.7

В реальной линейной электрической цепи обеспечить отрицательную индуктивность невозможно, поэтому L2 = – M является только расчетной величиной. В отличие от исходной в полученной схеме магнитная связь заменена гальванической. А это означает, что расчет такой схемы может быть осуществлен любым известным методом.