3.11. Расчет сложных электрических цепей комплексным методом

Расчет сложных линейных электрических цепей синусоидального тока комплексным методом осуществляется с помощью всех известных методов теории линейных электрических цепей постоянного тока. Все методы применимы в общем случае без ограничений.

Рис. 3.10

Пример. Записать систему уравнений, составленных по законам Кирхгофа, методам контурных токов и узловых потенциалов для электрической схемы, представленной на рис. 3.10.

Решение.

По законам Кирхгофа

Метод контурных токов

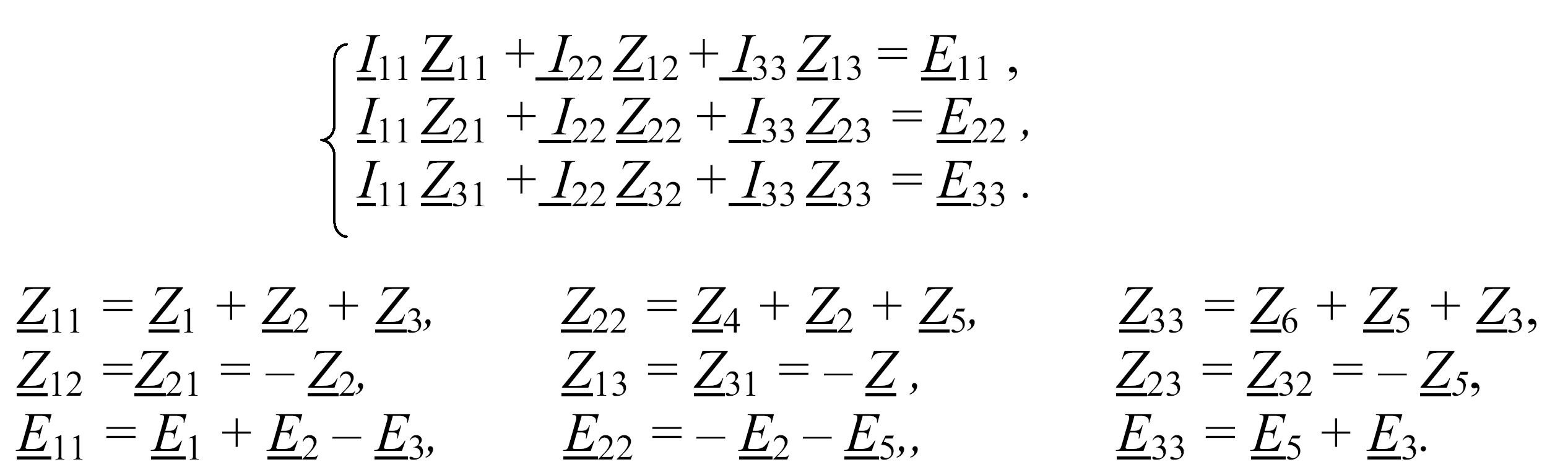
Метод узловых потенциалов

Расчет линейных электрических цепей синусоидального тока в установившемся режиме комплексным методом аналогичен расчету электрических цепей постоянного тока и производится по алгебраическим уравнениям, составленным по методам, основанным на закоах Ома и Кирхгофа.

Алгоритм расчета комплексным методом

1. Мгновенные значения напряжения источников ЭДС, токов источников тока заменяют соответствующими комплексными величинами

2. В зависимости от выбранного метода расчета вычисляют комплексные сопротивления или комплексные проводимости ветвей

Выбор рационального метода расчета сложной электрической цепи осуществляется, исходя из поставленной задачи и особенностей физической модели цепи, представленной в виде электрической схемы. Все рекомендации по выбору расчетных методик для цепей постоянного тока применимы и к выбору расчетных методик в комплексной форме для цепей синусоидального тока.

3. Составляют алгебраическое уравнение или систему алгебраических уравнений с комплексными коэффициентами и решают относительно искомой комплексной величины, например, тока

4. При необходимости осуществляют переход от комплексных величин к мгновенному значению

Глава 4. Резонансные явления в линейных электрических цепях

Явление в электрической цепи, содержащей участки, имеющие индуктивный и емкостной характер, при котором разность фаз синусоидального электрического напряжения и синусоидального электрического тока на входе цепи равна нулю, называют резонансом (ГОСТ Р52002-2003).

Пусть имеется цепь, изображенная на рис. 4.1:

Рис.

Условие резонанса для такой цепи

(4.1)

Различают резонанс напряжений и резонанс токов.

4.1. Резонанс напряжений

Резонансом напряжений называют явление резонанса в участке электрической цепи, содержащей последовательно соединенные индуктивный и емкостной элементы (ГОСТ Р52002-2003).

Определим полное комплексное сопротивление R, L, C цепи (рис. 4.2)

Рис. 4.2

где

(4.2)

Условие (4.1) = 0 выполнимо, если в выражении (4.2) соблюдается условие

что равносильно

(4.3)

Отсюда следует, что резонанса можно достичь изменением частоты, индуктивности, емкости:

(4.4)

Частоту 0 называют резонансной частотой (L и C заданы), соответственно L0 и C0 – резонансными индуктивностью и емкостью. Выполнение условия равенства индуктивного и емкостного сопротивлений (4.3) для последовательной цепи означает, что и напряжения на этих участках цепи будут одинаковы по модулю

Условие (4.3) , справедливое для цепи с последовательно соединенными R, L, C элементами, может быть переписанов виде условия резонанса напряжений для любой цепи

(4.5)

Ток в последовательной R, L, C цепи можно определить

В режиме резонанса это выражение сводится к При этом ток I имеет максимальное значение. Если реактивные сопротивления XC = XL при резонансе превосходят по значению активное сопротивление R, то напряжения на индуктивности и емкости могут значительно превысить напряжение на сопротивлении и, следовательно, на входе цепи. Поэтому резонанс при последовательном соединении называют резонансом напряжений.

63

Векторные диаграммы для трех режимов работы: дорезонансного, резонансного, послерезонансного – приведены на рис. 4.3.

Рис. 4.3

Свойства резонансного контура могут быть описаны с помощью волнового сопротивления, добротности, затухания.

Волновое сопротивление контура определяется величиной реактивного сопротивления емкости или индуктивности в момент резонанса:

Волновое сопротивление резонансного контура , [Ом] определяется индуктивностью, емкостью и не зависит от частоты приложенного напряжения.

Добротность – безразмерная величина, показывающая, во сколько раз напряжение на реактивном элементе больше входного (или на активном сопротивлении), если цепь находится в режиме резонанса

Затухание – безразмерная величина, обратная добротности

Зависимости полного, реактивного, активного сопротивлений или проводимостей цепи, угла разности фаз от частоты называют частотными характеристиками (рис. 4.4).

Рис. 4.4

где

Если R = 0, то цепь становится чисто реактивной и ее проводимость

Рис. 4.5

Реактивная проводимость В() (рис. 4.5) при R=0 имеет три характерные частоты – два нуля (при = 0, = ) и один полюс (при = 0). По характеру кривой В() можно заметить, что с увеличением частоты В убывает:

так как

Частотные характеристики I(), UR(), UL(), UC() называют резонансными кривыми (рис. 4.6).

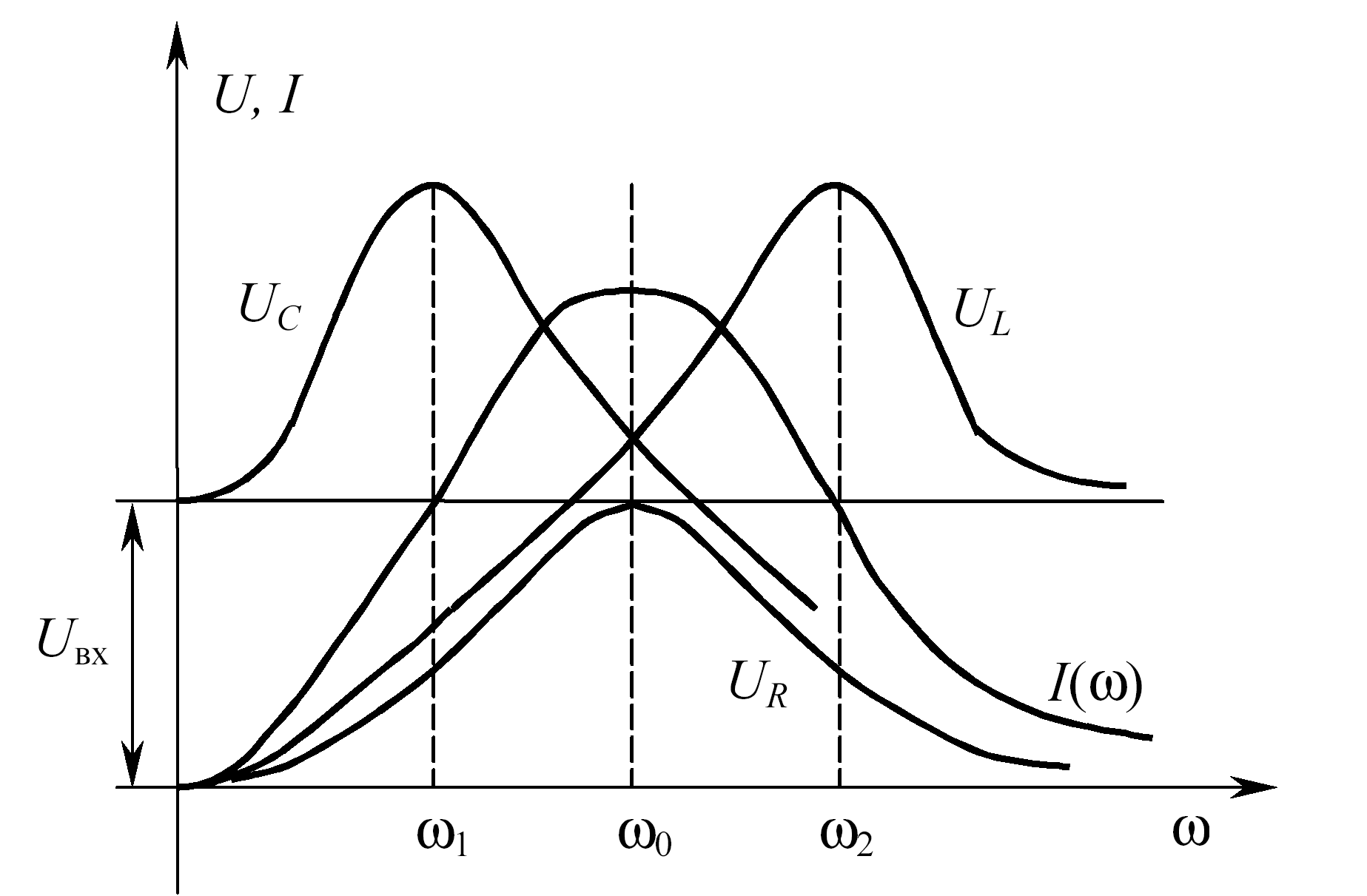
Рис. 4.6

Пусть Uвх = const, тогда

При = 0 I = 0, так как конденсатор не пропускает постоянный ток. При = I = 0, так как сопротивление катушки бесконечно большое. Максимум тока наблюдается при = 0, так как Z имеет минимальное значение, равное R. Напряжение на активном сопротивлении R

повторяет характеристику тока в масштабе напряжения.

Напряжение на емкости С

При = 0 все входное напряжение приложено к конденсатору, так как ХС , тогда как при и напряжение на конденсаторе стремится к нулю. Максимум UC наступает при частоте, меньшей 0, так как для получения UC необходимо ток I умножить на убывающую величину

Напряжение на индуктивности

Поведение характеристики UL() можно проанализировать аналогичным образом, что и поведение характеристики UС(). Экстремумы UL() и UС (), так же как и экстремумы В(), наступают при причем

Для сопоставления качества резонансных цепей резонансные кривые тока строят в относительных координатах (рис.4.7).

Рис. 4.7

(4.6)

Полоса пропускания – это диапазон частот, при которых относительный ток I/I0 не меньше некоторой величины, называемой уровнем полосы пропускания. Пусть (рис. 4.7), тогда полосу пропускания можно определить как диапазон частот, при которых в цепи выделяется мощность не меньше половины максимальной, т.е. мощности в момент резонанса

Полосу пропускания можно определить с помощью выражения (4.6), приравняв его к величине

В этом случае слагаемое под корнем должно быть равно 1, где – так называемая обобщенная расстройка, равная 1.

Из (4.6) следует, что и, следовательно, = arctg a = 45 °. Таким образом, на границах полосы пропускания обобщенная расстройка равна 1, а угол сдвига фаз составляет 45 °.