3.7. Комплексная проводимость

Комплексная электрическая проводимость – комплексная величина, равная отношению комплексного действующего значения синусоидального электрического тока в пассивной электрической цепи или ее элемента к комплексному действующему значению синусоидального электрического напряжения на выводах этой цепи или на этом элементе (ГОСТ Р52002-2003).

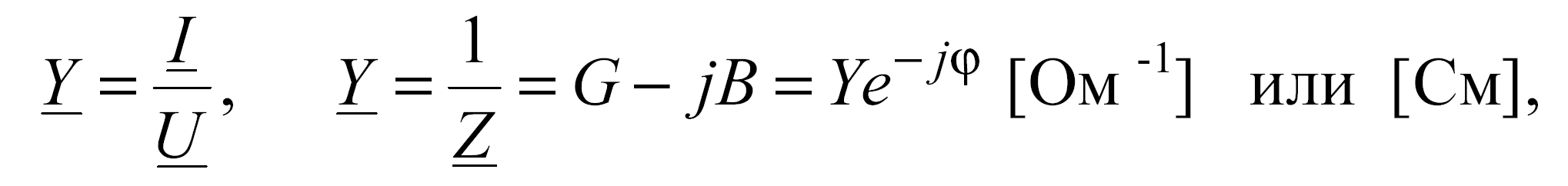где

3.8. Треугольник сопротивлений и треугольник проводимостей

Треугольник сопротивлений можно получить из векторной диаграммы цепи с последовательно соединенными участками активного, индуктивного и емкостного характера (рис. 3.4).

Рис. 3.4

Последовательность построения векторов указана в окружностях. Если все напряжения, составляющие векторную диаграмму, поделить на одну и ту же величину, очевидно, что получим такую же диаграмму, только в измененном масштабе. Если в качестве такой величины выбрать значение тока, который одинаков для всех элементов последовательной цепи, то получим соответствующие сопротивления. Учитывая, что сопротивления имеют скалярный характер, получим так называемый треугольник сопротивлений, где

; (рис. 3.5).

Рис. 3.5

Аналогично, рассматривая векторную диаграмму токов электрической цепи с параллельно соединенными активным, индуктивным и емкостным элементами (см. раздел 2.9), получим треугольник проводимостей (рис. 3.6)

Рис. 3.6

3.9. Законы Кирхгофа в комплексной форме

Первый закон Кирхгофа в комплексной форме записи

Второй закон Кирхгофа в комплексной форме записи

3.10. Активная, реактивная и полная мощности

Под активной мощностью Р в электрической цепи синусоидального тока понимают величину, равную среднеарифметическому значению мгновенной мощности за период (ГОСТ Р52002-2003)

(3.11)

где р = ui – мгновенное значение мощности.

Пусть u = Um sin (t + u),

i = Im sin (t + i).

Если принять u=0, то = u - i= - i , т. е. i = - ;

u = Um sin t,

i = Im sin (t - ).

Подставим выражения для мгновенных значений i и u в (3.11)

и воспользуемся известным тригонометрическим соотношением

получим

Рассмотрим способ определения активной и реактивной мощностей в комплексной форме записи. Пусть напряжение на участке цепи

а ток 

Учитывая, что для определения активной и реактивной мощностей следует использовать разность фаз , которая рассчитывается в виде при вычислении комплексной мощности в виде произведения комплексных чисел комплекс тока следует взять сопряженным.

Комплексная мощность – комплексная величина, равная произведению комплексного действующего значения синусоидального электрического напряжения и сопряженного комплексного действующего значения синусоидального электрического тока (ГОСТ

Р52002-2003).

где – активная мощность, [ВАр] – ре-

активная мощность – величина, равная при синусоидальном электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током (ГОСТ Р52002-2003);

– модуль полной комплексной мощности или просто полная мощность [ВА] – величина, равная произведению действующих значений электрического тока и электрического напряжения на входе двухполюсника (ГОСТ Р52002-2003).

Рис.3.7

Такой же результат по определению активной, реактивной и полной мощностей можно получить из анализа векторной диаграммы активно-реактивной цепи, например, цепи с последовательным соединением R, L, C элементов (рис. 3.4).

Если стороны полученного векторного треугольника напряжений: UR,

(UL-UC), U – умножить на одну ту же величину, например, ток I, то получим подобный треугольник мощностей (рис. 3.7), где

Активная мощность физически представляет собой энергию, которая выделяется в единицу времени в виде теплоты в резисторе R и измеряется с помощью ваттметра

Реактивная мощность Q = UIsinпропорциональна энергии, которая идет на создание электрического и магнитного поля емкости и индуктивности и измеряется с помощью счетчиков реактивной энергии. Модуль полной мощности S может быть найден с помощью амперметра и вольтметра, тогда как ваттметр измеряет активную мощность (рис. 3.8).

Рис.3.8

Множитель cosв выражении для подсчета активной мощности называют коэффициентом мощности. Коэффициент мощности – скалярная величина, равная отношению активной мощности к полной (ГОСТ Р52002-2003). Так как cos1, то и РUI. Электрическое оборудование, в том числе и электрические машины, рассчитано на определенное напряжение U, обусловленное типом и качеством изоляции, и на определенный ток, обусловленный допустимым нагревом проводников. Наивысшее использование свойств электротехнических устройств будет в случае, когда cosравен единице.

Методы повышения cos:

а) естественный – работа энергетического оборудования в номинальном режиме,

б) искусственный – установка компенсирующих устройств. Так, при индуктивном характере нагрузки в качестве компенсаторов используют батареи конденсаторов либо специальные электрические машины – синхронные компенсаторы.

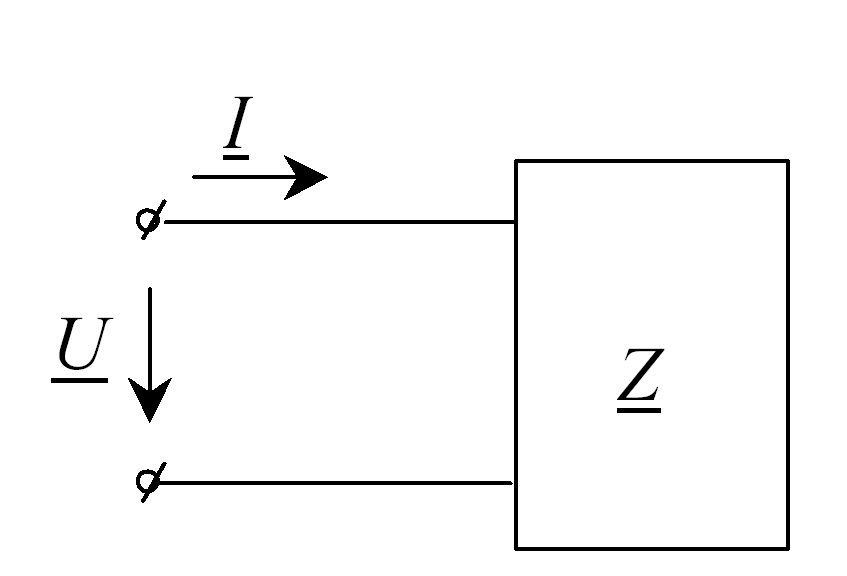
Рис.3.9

Пример. Определить S, Q, P для цепи, представленной на рис. 3.9 при

Решение.

1) Первый способ:

= (10 +j20)(1 –j5) =10 + j20 – j50 – j2100 = 90 – j30 , BA.

P = 90 Вт, Q= – 30 ВАр , 30 90 S ВА.

2) Второй способ:

= (10 -j20)(1 + j5) = 10 + j50 – j20 – j2100 = 90 + j30 , BA.

P = 90 Вт, Q = 30 ВАр, ВА.

Таким образом, как первый, так и второй способы дают одинаковые результаты расчета полной и активной мощности, тогда как реактивная мощность отличается только знаком.