Лабораторное занятие №8.

Лабораторная работа №8. Резонанс токов.

Цель работы: изучение электрических процессов, происходящих в цепи переменного тока, при параллельном соединении катушки и конденсатора.

1.Краткие теоретические сведения.

Резонанс токов. При рассмотрении параллельного соединения катушки и конденсатора был отмечен случай равенства активной и реактивной проводимостей B_L = Вc элементов, содержащих индуктивность и емкость.

В этом случае электрическая цепь находится в режиме резонанса токов, который характеризуется тем, что реактивная мощность цепи равна нулю, ток и напряжение совпадают по фазе (φ = 0).

Так же как и резонанс напряжений, резонанс токов возникает, когда частота источника энергии равна резонансной частоте ω_р , а B_L = Вс.

Режим электрической цепи при параллельном соединении участков с

индуктивностью и емкостью, характеризующийся равенством индуктивной и емкостной проводимостей, называют резонансом токов.

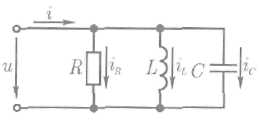
Сначала рассмотрим этот режим для схемы идеализированной цепи

а)

б) в)

(рис. 1.1.а, б, в). В этой схеме параллельно резистору R включены идеальные катушки L и конденсатор С, потери энергии в которых не учитываются.

Реактивные проводимости зависят от частоты вынужденных колебаний. Тогда, активная проводимость: G=1/R,

реактивные проводимости: B_L=1/ωL; B_C=ωC.

При резонансе токов:

B_L=B_C; ω=ω_P; .

Отсюда определяют резонансную частоту ω_P=1/

Выражение для резонансной частоты в данном случае такое же, какое было получено при рассмотрении резонанса напряжений и для частоты собственных колебаний в контуре без потерь.

Резонанс токов, так же как и резонанс напряжений, можно получить изменением параметров L и С или изменением частоты источника энергии.

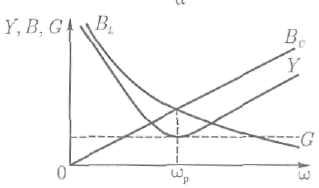
Резонансные кривые

На рис. 1.1 б показаны зависимости проводимостей от частоты. Полная проводимость цепи при резонансной частоте оказывается наименьшей, равной активной проводимости G. При изменении частоты в обе стороны от резонансной полная проводимость увеличивается.

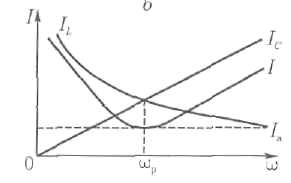
При резонансе токов отношение тока индуктивного или емкостного к току в неразветвленной части цепи равно отношению волновой проводимости Y_B=1/Z_B= к активной проводимости цепи G.

Добротность контура

При параллельном соединении элементов качество резонансной цепи считается тем выше, чем больше отношение Y/G, которое и в этом случае называется добротностью

Q=Y/G= .

Чем меньше потери энергии в цепи (этому соответствует большая величина R), тем больше добротность.

Параметры реальных катушек и конденсаторов (R, L, С) измеряются и задаются в справочниках применительно к их схемам замещения с последовательным соединением активных и реактивных элементов.

2.Порядок выполнения работы:

2.1.Соберите электрическую схему согласно рисунку:

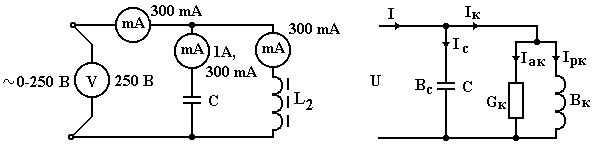
Показываем собранную схему преподавателю.

2 .2.Убедитесь, что ручка регулятора «U» находится в крайнем левом положении. Выключите питание и установите U_вх=90 В. Изменяя емкость батареи конденсаторов от 0 до 17 мкФ, снимите показания приборов, данные занесите в таблицу измерений 1.

2.3.Показания приборов выставить на «0». Отключить источник питания.

2.4. По данным измерений рассчитайте параметры электрической цепи при резонансе токов, результаты расчетов занесите в таблицу измерений 2.

2.5. Постройте в выбранном масштабе резонансные кривые.

3. Отчет о лабораторной работе должен включать:

• Принципиальную электрическую схему;

• Таблицу экспериментальных данных;

• Расчет параметров электрической цепи;

• Векторную диаграмму резонанса токов;

• Резонансные кривые, построенные в масштабе;

• Ответы на контрольные вопросы.

4. Контрольные вопросы

1. Что называется резонансом токов? Запишите условие резонанса токов.

2. Где и в каких устройствах используется явление резонанса токов?

3. Определите резонансную частоту через параметры колебательного контура.

4. Найдите добротность экспериментального контура.

5. Как влияет величина активного сопротивления катушки на вид резонансных кривых?

6. Почему по мере приближения к резонансу потребляемый контуром ток уменьшается?

7. Почему для повышения коэффициента мощности используется явление резонанса токов, а не резонанса напряжений?

8. Что называется входным сопротивлением контура?

9. Как зависит входное сопротивление контура от добротности катушки?

10. Каким из элементов контура (катушка, конденсатор) определяется в большей степени добротность контура?

11. Изобразите на векторной диаграмме годограф потребляемого тока при изменении емкости конденсатора.

12. Почему на повышенных частотах катушки индуктивностей изготовляют с ферритовыми сердечниками, а не с магнитопроводами из пластин электротехнической стали?

13. Почему входное сопротивление цепи, состоящей из параллельного соединения катушки и конденсатора, в момент резонанса является максимальным?

14. Какую величину называют «волновым сопротивлением контура»?

15. Какую величину называют затуханием контура?