Тема 4: Колебательный контур. Резонанс напряжений, резонанс токов». Лабораторное занятие № 6.

Лабораторная работа №7. Резонанс напряжения.

Цель работы: изучение электрических процессов, происходящих в цепи переменного тока при последовательном соединении катушки и конденсатора.

1.Краткие теоретические сведения.

Совпадение частоты вынужденных колебаний, сообщаемых извне физической системе, с частотой собственных колебаний системы называется резонансом. В электрической цепи резонанс возникает при совпадении частот источника переменного тока и собственных свободных колебаний электрической цепи.

Если в цепи переменного тока с последовательно соединенными конденсатором ёмкостью С и катушкой с сопротивлением R и индуктивностью L равны реактивные сопротивления X, то в цепи наступает резонанс напряжений, который характеризуется тем, что реактивная мощность цепи равна нулю, ток и напряжение совпадают по фазе.

Условием резонанса напряжений является равенство: .Частота свободных колебаний цепи равна: .(1)

Настроить контур в резонанс напряжений можно тремя способами: изменяя частоту ; изменяя значение L или подстраивая значение C.

Идеальный резонанс напряжений при R=0 эквивалентен короткому замыканию.

Явление резонанса можно наблюдать в любых колебательных системах, в том числе механических и электрических. Электрический резонанс возникает при определенных условиях в электрических цепях переменного тока, содержащих индуктивности и емкости.

Изучение электрического резонанса необходимо, так как это явление широко используется в технике электросвязи, а в установках сильного тока, где его возникновение специально не предусматривается, резонанс может оказаться опасным (могут возникнуть перенапряжения и пробой изоляции).

Колебательный контур с потерями энергии.

Незатухающие колебания в контуре получаются в предположении, что потери энергии отсутствуют, т.е. R = 0.

Если активное сопротивление контура не равно нулю, то запас энергии в контуре сокращается (энергия превращается в теплоту), амплитуды тока и напряжения с каждым периодом убывают.

Более детальное исследование колебательного контура показывает, что частота собственных колебаний зависит от активного сопротивления:

ω₀=

При R = 0 это выражение совпадает с (1).

При R > то, колебания в контуре не возникают. В этом случае процесс в контуре после подключения конденсатора к катушке является периодическим, напряжение на конденсаторе с максимальной величины постепенно падает до нуля, а ток сначала растет, а потом тоже падает до нуля, не меняя знака.

В связи с этим большой практический интерес представляют зависимости напряжений и токов на отдельных элементах цепи от частоты. Эти зависимости называют резонансными кривыми (рис. 1, в).

Реактивные сопротивления с изменением частоты меняются, как показано на рис. 1, б. При увеличении частоты I увеличивается пропорционально частоте, а Х_с уменьшается по закону обраной пропорциональности.

Соответственно полное сопротивление Z цепи при резонансной частоте ω_р оказывается наименьшим, равным активному сопротивлению R.

Такая зависимость полного сопротивления от частоты определяет характер изменения тока при постоянном напряжении в цепи (см. рис. 1, в). Увеличение частоты ведет к увеличению U_L, которое при частоте, несколько большей резонансной, достигает максимума, а затем уменьшается до величины напряжения источника разрыву цепи на зажимах катушки.

При частотах, меньших резонансной, реактивное сопротивление цепи имеет емкостный характер (отрицательно), поэтому и угол сдвига фаз в цепи отрицательный. Уменьшаясь с ростом частоты, он становится равным нулю при резонансе (I_p = 0), а затем меняет знак и увеличивается при дальнейшем увеличении частоты.

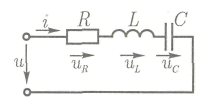
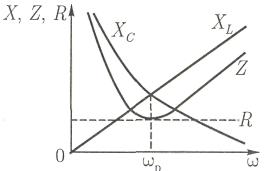
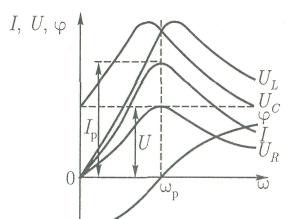
^{Рис.1.(а, б, в)}

Резонанс напряжения рассмотрим сначала на схеме идеализированной цепи (рис. 1.а), в которой последовательно с резистором R включены идеальные (без потерь) катушка L и конденсатор С.

Реактивные сопротивления X_L и Х_с (рис. 17.4, б) зависят от частоты вынужденных колебаний ω:

X_L=ωL, X_C=1/ωC,

Приравнивая реактивные сопротивления и учитывая, что ω = ω_р, по­лучим

_pL= .

Отсюда резонансная частота

_p= ; f_p= .

В данном случае выражение для резонансной частоты совпадает с формулой для частоты собственных колебаний в контуре без потерь.

Нужно отметить, что в неразветвленной цепи обмен энергией между катушкой и конденсатором совершается через источник энергии, который восполняет потери энергии в активных сопротивлениях.

Добротность контура. При резонансе напряжений отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи (напряжению источника), равно отношению волнового сопротивления к активному. Действительно, при резонансе сопротивления реактивных элементов

_pL= = = =Z_В.

Поэтому

U_L= U_C=I Z_В= Z_В; = = .

Из этого выражения следует, что при Zв> R напряжение на реактивных элементах больше напряжения источника.

Такое превышение может оказаться значительным, если реактивные сопротивления много больше активного и изоляция катушки или конденсатора может быть пробита. На практике подобный случай возможен, если на конце кабельной линии включается приемник, обладающий индуктивностью.

В радиотехнике качество резонансного контура считается тем выше, чем больше отношение Zв/R, называемое добротность к контура Q:

Q= = = = .

Чем меньше мощность потерь энергии в контуре, тем больше добротность контура.

Большему значению добротности соответствуют больший ток Iр при резонансе и более острая резонансная кривая.

2. Порядок выполнения работы:

2.1. Соберите электрическую схему согласно рисунку:

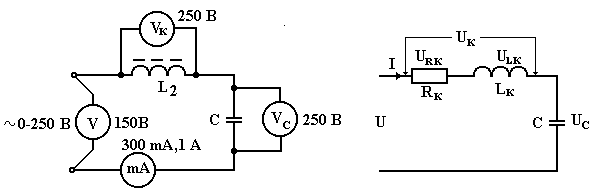
Показываем собранную схему преподавателю.

2.2.Установите переключатель блока питания “0-250 В” в положение “переменный ток ”, ручку регулятора “U” в крайнее левое положение. Нажмите кнопку включения питания, вращая ручку регулятора “U”, установите входное U равное 50 В.

2.3.Изменяя емкость конденсаторов батареи в пределах от “0” до “18” мкФ, снимите показания приборов. Данные занесите в таблицу 1

2.4.Показания приборов выставить на «0».

2.5. Отключить источник питания.

2.6. По данным измерений рассчитайте параметры электрической цепи, расчеты занесите в таблицы 1,2.

2.7. Постройте в выбранном масштабе резонансные кривые.

3.Отчет о лабораторной работе должен включать:

• Принципиальную электрическую схему;

• Таблицы экспериментальных данных;

• Расчеты параметров электрической цепи;

• Векторную диаграмму резонанса напряжений;

• Резонансные кривые, построенные в масштабе;

• Ответы на контрольные вопросы.

4. Контрольные вопросы.

1. Что называется резонансом напряжений? Запишите условие резонанса напряжений.

2. Приведите примеры использования явления резонанса напряжений в электротехнике.

3. Изобразите векторную диаграмму резонанса напряжений?

4. Определите добротность колебательного контура по экспериментальным данным?

5. Изменением каких параметров можно добиться резонанса напряжений?

6. Какая из резонансных кривых будет называться частотной характеристикой контура?

7. Объясните появление большего напряжения на реактивных элементах последовательного соединения катушки и конденсатора, чем напряжение сети? Возможно ли такое явление в цепи постоянного тока?