2

ФЕДЕРАЛЬНОЕ АГЕНСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ ПО РЫБОЛОВСТВУ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

КОЛЛЕДЖ

Сборник описаний

лабораторных работ по курсу

«ЭЛЕКТРОТЕХНИКА»

для студентов специальностей:140212.51 «Электроснабжение»

140613.51 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования»

Мурманск

2007

Тема 3: «Цепи с r, l, c. Соединения в цепи: последовательное и параллельное». Лабораторное занятие №6.

Лабораторная работа №3. Исследование работы цепи последовательного соединения R и L, R и C.

Цель работы: изучить особенности цепей переменного тока включающих в себя резистор, конденсатор и катушку индуктивности, научиться производить расчеты, строить и анализировать векторные, волновые и топологические диаграммы.

1.Краткие теоретические сведения.

Резистор- элемент электрической цепи, который в основном обладает активным сопротивлением и в котором происходит преобразование электрической энергии в тепловую энергию.

Катушка представляет собой индуктивный элемент электрической цепи, который обладает индуктивным сопротивлением переменному току.

Конденсатор является емкостным элементом электрической цепи и обладает емкостным сопротивлением протекание переменного тока. Индуктивное и емкостное сопротивления называются реактивными сопротивлениями. Катушка и конденсатор не преобразуют электрическую энергию в другие виды энергии, поэтому их сопротивления называются реактивными.

Резисторы, катушки и конденсаторы представляют собой реальные элементы электрических цепей. Если предполагается, что резистор обладает только активным сопротивлением, катушка только индуктивным, конденсатор только емкостным сопротивлением, такие элементы электрической цепи называются идеальными: идеальный резистор, идеальная катушка, идеальный конденсатор.

Однако при более строгих расчетах любой реальный элемент электрической цепи изображается на электрической, схеме комбинацией соединения идеальных элементов.

Под терминами резистор, катушка, конденсатор в разговорной речи часто понимается их идеальные аналоги.

Из теории электрических цепей переменного синусоидального тока известно, что ток, протекающий по идеальному резистору, совпадает по фазе с приложенным напряжением, ток, протекающий по идеальной катушке, по фазе колебания отстает на 90° от приложенного напряжения; ток, протекающий по идеальному конденсатору, опережает по фазе колебания на 90° приложенное напряжение.

При последовательном соединении R и L, R и С, ток, потребляемый электрической цепью, не совпадает по фазе с приложенным напряжением на угол, который определяется соотношением параметров активного и реактивного сопротивления.

Исследование схемы последовательного соединения катушки, резистора.

Реальная катушка c индуктивностью L не является идеальной, поэтому ее схема замещения включает последовательно включенные резистор R и идеальную катушку индуктивности L.

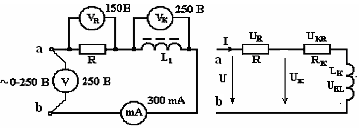
Заметим, что в эксперименте (метод измерения параметров катушки называется метод трех вольтметров) определяются значения напряжений: питания U на резисторе U_R, а также на клеммах реальной катушки U_L, в то время как активная U_RL и реактивная U_RL составляющие напряжения схемы замещения катушки рассчитываются по результатам эксперимента

Цепь с активным сопротивлением R и индуктивностью L.

Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток (рис.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки

Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенным активным сопротивлением R и индуктивным сопротивлением X (рис. 1).

Активное напряжение совпадет по фазе с током. Индуктивное напряжение опережает ток на угол 90°.

Реальная катушка отличается от идеальной тем, что переменный ток в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в теплоту в соответствии с законом Ленца - Джоуля.

Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле - реактивной мощностью Q. В реальной катушке имеют место оба процесса, т.е. ее активная и реактивная мощности отличны от нуля. Поэтому в схеме замещения реальная катушка должна быть представлена активным и реактивным элементами.

Деление реальной катушки на два элемента искусственно, так как конструктивно оба элемента неразделимы. Однако такой же схемой замещения можно представить реальную цепь из двух конструктивно не совмещенных элементов, один из которых характеризуется только активной мощностью Р (Q = 0), а другой - реактивной (индуктивной) мощностью Q (Р = 0).

В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.

Активное сопротивление определяется величиной мощности потерь R= , а индуктивность - конструкцией катушки.

Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи.

Z=

Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими значениями напряжения и тока формулой, подобной формуле, выражающей закон Ома.

U=I =IZ; I= .

Cos= ;Sinφ =

Рис. 1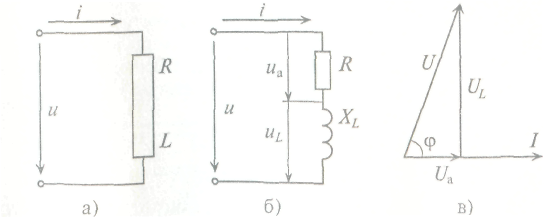

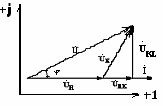
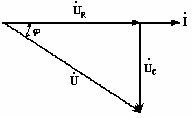
Построение векторной диаграммы на комплексной плоскости производится следующим образом. Произвольно принимается, что вектор Ů_R направлен по действительной оси +1. Туда же направлен и вектор тока İ, и вектор напряжения Ů_КR как активная составляющая вектора Ů_К. Поскольку резистор R_K (формально) следует за резистором R, то на топографической векторной диаграмме (в отличие от просто векторной) начало вектора Ů_КR связано с концом вектора Ů_КR, аналогично: начало вектора U_KL cвязано с концом вектора началом Ů_КR. Вектор Ů, начинающийся из точки а, как точки

наиболее высокого потенциала, своим концом упирается в окончание вектора Ů_К (точка b).

а) б) в)

Рис. 1.1. Принципиальная электрическая схема (а) последовательного соединения резистора и катушки, схема замещения (б), топологическая векторная диаграмма (качественная) напряжений и тока (в).

Следует учитывать, что:

 напряжение на резисторе R равно U_R = IR, т.е. R = U_R/I (вектор напряжения совпадает с вектором тока);

 из треугольника напряжений (рис.1.1, в) имеем (с учетом известной формулы треугольника): сos = (U² + U_R² U_K²)/(2U U_R);

 из треугольника напряжений (рис.1.1, в) получаем, что активная составляющая напряжения U_KR на катушке равна: U_KR = Uсos U_R;

 активная составляющая R_K сопротивления катушки: R_K = U_RK/I;

 реактивная составляющая напряжения U_KL = Usin;

 реактивное сопротивление катушки: X_L = U_L/I;

 полное сопротивление катушки: Z_K = (X_L² + R_K²);

 величина индуктивности L = X_L/ω= XL/2πf.

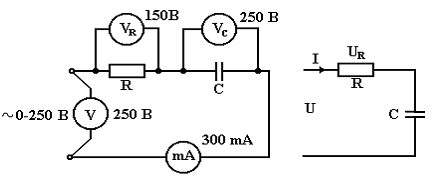
Исследование схемы последовательного соединения конденсатора и резистора.

Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток i=I_msinωt то он создает падение напряжения на активном сопротивлении u_a=U_msinωt и на емкостном сопротивлении u_c=U_msin(ωt-π/2). Векторная диаграмма для этой цепи изображена на рис. 1.2.б.

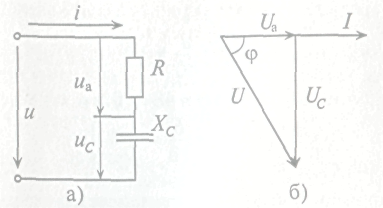
Рис. 1.2.

Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол φ < 90.

В конденсаторе с идеальным диэлектриком предполагается полное отсутствие тока проводимости и потерь энергии. Изменение напряжения между обкладками конденсатора сопровождается электрическим током смещения, величина которого зависит от емкости С.

Заряд конденсатора пропорционален напряжению между его об­кладками, поэтому изменение напряжения сопровождается изменением заряда dq = Cdu.

При этом во внешнем по отношению к конденсатору участке цепи происходит движение электронов (ток проводимости) через источник. Одновременно при увеличении напряжения совершается поляризация диэлектрика в конденсаторе и возникает ток смещения. При уменьшении напряжения диэлектрик деполяризуется.

Таким образом, ток в цепи с конденсатором пропорционален скорости изменения напряжения на его обкладках.

При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток). Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.

Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в теплоту, скорость которой выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.

Деление реального конденсатора на два элемента - это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой - реактивной (емкостной) мощностью Q (Р = 0).

Реальный конденсатор так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Хс сопротивлениями.

Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью С.

В данном случае считается, что конденсатор является идеальным и его схема замещения представлена на рис.1.3, б.

а) б) в)

Рис.1.3. Принципиальная электрическая схема (а) последовательного соединения резистора и конденсатора, схема замещения (б), топологическая векторная диаграмма (качественная) напряжений и тока (в)

С учетом топологической векторной диаграммы (рис.1.3, в) для данной схемы следует учитывать (вывести самостоятельно), что:

R = U_R/I_R = U_R/I;

X_C = U_С/I; С =1/2πfX_C;

Cos  = U_R/U.

2. Порядок выполнения работы:

2.1.Соберите электрическую схему в соответствии с выверенной монтажной схемой согласно рисунку:

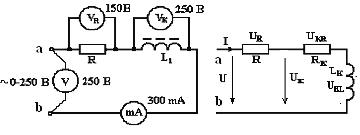
Показываем собранную схему преподавателю.

2 .2. Установите переключатель блока питания «0-250В” в положение “переменный ток“, ручку регулятора “U”в левое крайнее положение. Нажмите кнопку включения источника питания и, вращая ручку регулятора напряжения вправо. Устанавливаем входное “U” по прибору U (180…250 В) по указанию преподавателя.

2.3. Снимите показания приборов и занесите их в таблицу 1.

2.4. Выключите источник питания и вместо катушки подключите к ранее собранной электрической цепи конденсатор. Электрическая схема согласно рисунку:

Показываем собранную схему преподавателю.

2.5. Повторите опыт, занесите данные измерений в таблицу 2.

2.6. Показания приборов выставьте на «0». Отключите источник питания.

2.7. Приведите в порядок рабочее место.

2.8. По опытным данным рассчитайте параметры электрической цепи при последовательном соединении R и L, R и C. Постройте в выбранном масштабе векторные, топологические и волновые диаграммы тока и напряжения.

3.Отчет о лабораторной работе должен включать:

• Принципиальную электрическую схему, схему замещения;

• Таблицы экспериментальных данных;

• Расчеты параметров электрических цепей;

• Векторные и волновые диаграммы, выполненные в масштабе;

• Ответы на контрольные вопросы.

4. Контрольные вопросы.

1. Что называется действующим значением переменного тока? Запишите формулу определения действующего значения тока.

2. Дайте определения мгновенного, амплитудного, среднего значений переменного синусоидального тока.

3. Что означают понятия: фаза колебания, начальная фаза, частота, круговая частота переменного синусоидального тока?

4. Что такое комплекс действующего значения тока, напряжения, ЭДС?

5. Что означают понятия: активное, индуктивное, полное сопротивления катушки?

6. Что называют добротностью катушки?

7. Как определяется сдвиг по фазе колебаний напряжения и тока?

8. Что понимают под активной, реактивной, полной мощностью цепи переменного синусоидального тока?

9. В каких единицах измеряется активная, реактивная, полная мощность цепи переменного синусоидального тока?

10. Что такое треугольник сопротивлений катушки?

11. Как называется метод определения параметров катушки, используемый в лабораторной работе?

12. Что такое идеальная катушка, реальная катушка?

13. Запишите формулы расчета активной, реактивной и полной мощности реальной катушки.

14. Что называется векторной диаграммой катушки?

15. Изобразите векторные диаграммы идеальной и реальной катушек

16. Запишите законы Ома для действующих и комплексных значений тока и напряжения реальной (идеальной) катушки.

17. Запишите формулы перехода от мгновенных значений синусоидально изменяющихся величин к их комплексным значениям и наоборот.

18. Изобразите годограф вектора тока реальной катушки при изменении индуктивности катушки от нуля до бесконечности.