10.5. Деформации жёсткой пластинки при изгибе
10.5.1. Связь между усилиями и деформациями (σx , σу ху = ух)
нормальные напряжения σx и σу, действующие по граням элементов, эквивалентны изгибающим погонным моментам Мх и Му (приходящимся на единицу ширины грани).
касательные напряжения ху и ух, действующие по граням элементов, эквивалентны погонным крутящим моментам Кху и Кух (приходящимся на единицу ширины грани).
Положительные направления осей системы координат и моментов показаны на рис. 10.7.
По граням элемента, как и в сечениях балки при поперечном нагибе, действуют касательные напряжения х и y (см. рис.10.7) от поперечных сил Qx и Qy. При расчётах они ввиду малой величины обычно не определяются.
Тождественность эпюр напряжений для обычной балки и для элемента пластинки позволяет установить связь между напряжениями и моментами
Рис. 10.7 Внутренние силовые факторы и напряжения, действующие по граням пластины
(10.2)
Так как напряжения ху и ух определяются для одной в той же точки слоя пластинки, то согласно закону парности они равны, поэтому равны и крутящие моменты Кху = Кyх .
Моменты инерции, как и изгибающие и крутящие моменты, относятся к единице ширины и поэтому
Максимальные величины напряжений:
(10.3)
Деформации слоев пластинки вычисляются на основании закона Гука для плоского напряжённого состояния
(10.4)
Здесь g – модуль сдвига;
γхy – относительный сдвиг.
10.5.2. Связь между моментами и кривизнами изогнутой поверхности пластинки.
Нанесём на срединную плоскость пластинки прямые ВС и ЕД (рис. 10.8), проходящие через точку А и параллельные соответственно осям X и y .
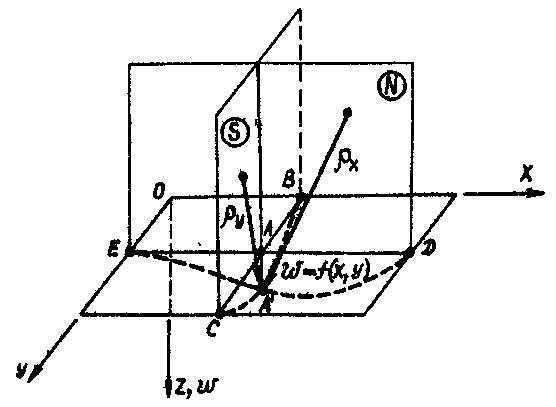
Рис.10.8. Криволинейная поверхность пластинки после деформации
После деформации изогнутая поверхность пластинки будет представлять собой криволинейную поверхность, которая описываются уравнением w = f(х,y), a точка A займет положение А'.
Приближённое значение кривизны линии ВАС и линии ЕАД по аналогии с кривизной изогнутой оси балки выражается соответственно как
Используем
также связь между удлинением волокна
изогнутой балки и её кривизной
.
Для слоев пластинки можно записать:
(10.5)
Здесь z - расстояние рассматриваемого слоя пластинки от нейтральной срединной поверхности.
В процессе деформации элементы пластинки не только изгибаются, но и закручиваются.
Определим относительный угол закручивания балки-полоски, шириной dх, выделенной из пластинки параллельно оси y (рисунок 10.9).
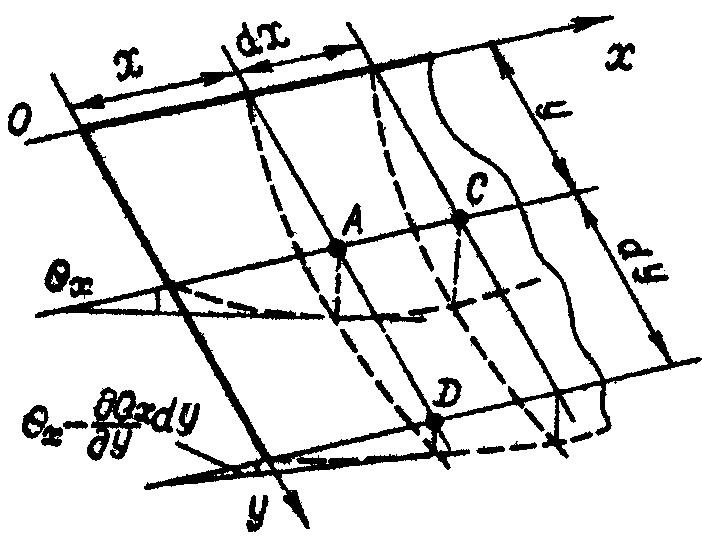
Рис. 10.9 Определение относительного угла закручивания балки-полоски
Угол наклона касательной θх к срединной поверхности в направлении оси x меняется при изменении координат х и у.
в
точке А
он
равен
,
а при приращении координаты у
на
величину dу
(точке d)
угол
наклона касательной будет равен
.
Приращение
угла на единице длины, то есть относительный
угол закручивания
равен
и называется кривизной
кручения
или просто кручением.
Аналогично можно определить кривизну кручения и при изменении угла θу в плоскости,. параллельной плоскости y0z , при увеличении координаты х.
П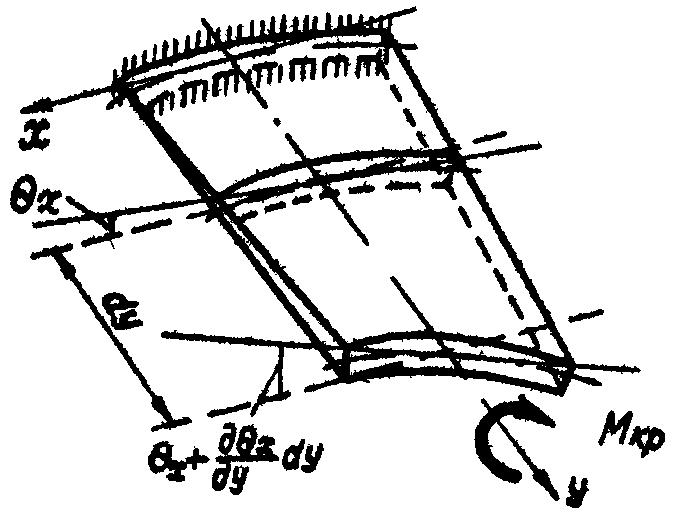
ри
рассмотрении кривизны кручения пластинки
удобно использовать
аналогию
с кручением тонкостенного стержня (рис.
10.10).
Установим зависимость между кручением и деформацией сдвига произвольного слоя, расположенного на расстоянии z от срединной плоскости.
рассмотрим элемент пластинки, который представлен срединной плоскостью абс и тремя нормалями к ней, восстановленными в концах взаимно перпендикулярных отрезков dx и dy (рис.10.11).
Рис. 10.10. Определение кривизны кручения
Рис.10.11. Деформация элемента пластинки при сдвиге
Нормаль аа' будем условно считать закреплённой, тогда вследствие кручения нормали bb' и сс повернутся вокруг прямых аb и ас соответственно на углы
и
.
Точка b' при этом переместится на расстояние zdx и займёт положение b. Этому расстоянию будет соответствовать угол γ = z. Аналогичный вывод будем иметь и по отношению к расстоянию сс и к углу γ.
Таким образом, полный угол сдвига у рассматриваемого слоя составит величину
.
Используя зависимость (10.4), получим:
. (10.6)
Из совместного решения уравнений (10.5) с учётом (10.1) будем иметь:
(10.7)
Выражение
же (10.6) при
приводится к виду
. (10.8)