35. Формирование электромагнитных колебаний в колебательном контуре.
Электромагнитные
колебания — это колебания электрических
и магнитных полей, которые сопровождаются
периодическим изменением заряда, тока
и напряжения. Простейшей системой, где
могут возникнуть и существовать
электромагнитные колебания, является
колебательный контур. Колебательный
контур — это система, состоящая из
катушки индуктивности и конденсатора
(рис. 41, а). Если конденсатор зарядить и
замкнуть на катушку, то по катушке
потечет ток (рис. 41, б). Когда конденсатор
разрядится, ток в цепи не прекратится
из-за самоиндукции в катушке. Индукционный
ток, в соответствии с правилом Ленца,
будет течь в ту же сторону и перезарядит
конденсатор (рис. 41, в). Ток в данном
направлении прекратится, и процесс
повторится в обратном направлении (рис.
41, г). Таким образом, в колебательном
контуре будут происходить электромагнитные
колебания из-за превращения энергии
электрического поля конденсатора
в энергию магнитного поля катушки с
током
, и наоборот.
Период электромагнитных колебаний в идеальном колебательном контуре (т. е. в таком контуре, где нет потерь энергии) зависит от индуктивности катушки и емкости конденсатора и находится по
формуле
Томсона
. Частота с периодом связана обратно
пропорциональной зависимостью
В реальном колебательном контуре свободные электромагнитные колебания будут затухающими из-за потерь энергии на нагревание проводов. Для практического применения важно получить незатухающие электромагнитные колебания, а для этого необходимо колебательный контур пополнять электроэнергией, чтобы скомпенсировать потери энергии. Для получения незатухающих электромагнитных колебаний применяют генератор незатухающих колебаний, который является примером автоколебательной системы.
36. Понятие электромагнитных волн, волновое уравнение для световой волны.
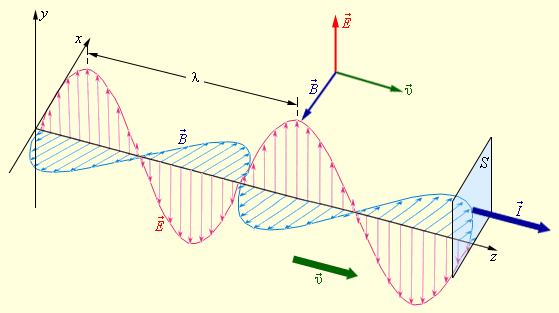
Электромагнитная волна - процесс распространения электромагнитного поля в пространстве.
Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.
Волновое уравнение
По своей физической природе световые волны являются волнами электромагнитными. Поэтому волновая оптика непосредственно основывается на уравнениях Максвелла.
Уравнения Максвелла связывают вектор напряженности электрического поля E и вектор электрической индукции D с вектором напряженности магнитного поля H и вектором индукции B. В отсутствие токов и свободных электрических зарядов они имеют вид:
где и - соответственно электрическая и магнитная постоянные, и - относительные соответственно диэлектрическая и магнитная проницаемости среды.
37. Связь параметров электрических и магнитных процессов в теории Максвелла
Существование электромагнитных волн было теоретически предсказано великим английским физиком Дж. Максвеллом в 1864 году. Максвелл проанализировал все известные к тому времени законы электродинамики и сделал попытку применить их к изменяющимся во времени электрическому и магнитному полям. Он обратил внимание на ассиметрию взаимосвязи между электрическими и магнитными явлениями. Максвелл ввел в физику понятие вихревого электрического поля и предложил новую трактовку закона электромагнитной индукции, открытой Фарадеем в 1831 г.:
Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты.
Максвелл высказал гипотезу о существовании и обратного процесса:
Изменяющееся во времени электрическое поле порождает в окружающем пространстве магнитное поле.
Рис. 2.6.1 и 2.6.2 иллюстрируют взаимное превращение электрического и магнитного полей.
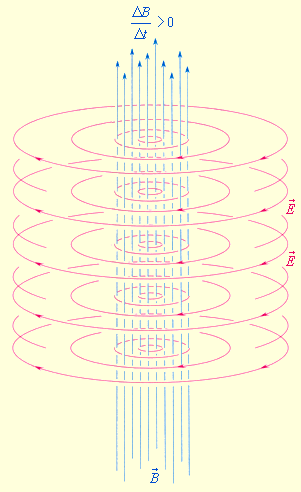
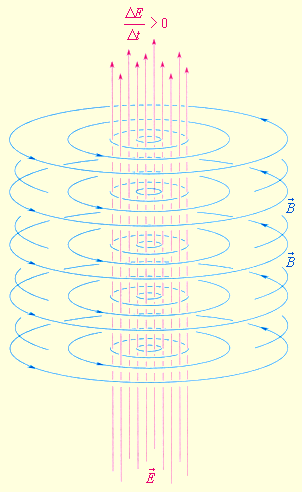
Эта гипотеза была лишь теоретическим предположением, не имеющим экспериментального подтверждения, однако на ее основе Максвеллу удалось записать непротиворечивую систему уравнений, описывающих взаимные превращения электрического и магнитного полей, т. е. систему уравнений электромагнитного поля (уравнений Максвелла). Из теории Максвелла вытекает ряд важных выводов:
1. Существуют электромагнитные волны, то есть распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы и перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны
