131

М инистерство образования и науки Украины

Национальный авиационный университет

Аэрокосмический институт

Кафедра конструкции летательных аппаратов

ЛЕКЦИЯ № 9 (3)

по дисциплине "Конструкция и прочность летательных аппаратов"

9. Определение нормальных и касательных напряжений.

Составитель проф. Радченко А.И.

Киев 2009

9. Определение нормальных и касательных напряжений.

Ниже излагается расчет нормальных напряжений в сечении кры­ла методом редукционных коэффициентов. Он был предложен и разработан в 1932 - 1935 гг. проф. В. Н. Беляевым.

9.1. Определение нормальных напряжений.

9.1.1. Основные допущения.

Современные методы определения нормальных напряжений в крыле самолета основаны на представлении крыла в виде тонкостенной балки. Аналогия крыла с балкой становится особенно понятной, если сопоставить их деформации. Как и для балки, деформации крыла большого удлинения характеризуются одним линейным (прогибом) и одним угловым (углом крутки) сме­щением. Как и в случае балки, нормальные напряжения в сечении крыла определяют при следующих до­пущениях (рис. 9.1):

1) плоские сечения п - п, нормальные к оси z крыла, поворачи­ваясь при деформации (n' - n'), остаются плос­кими;

2) в продольных сечениях панелей крыла нормальные напряжения σ_х = 0;

3) крыло рассматривается как безмоментная тонкостенная оболочка.

Первых два допущения обосновыва­ются наличием в крыле часто располож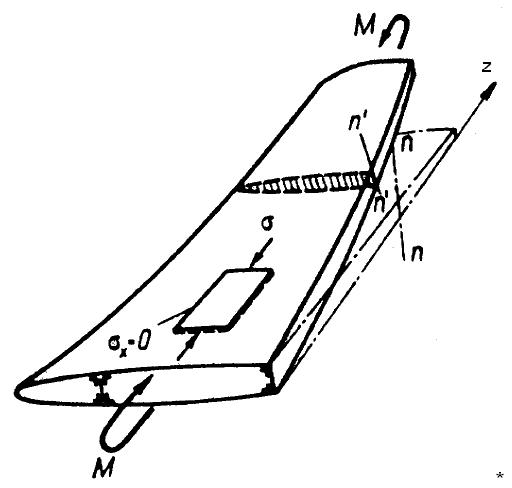 енных нервюр, которые, соединяя раз­личные элементы крыла, обеспечивают его работу, как единого це­лого.

Благодаря большой жесткости нервюр в своей плоскости кон­тур поперечного сечения крыла не деформируется при изгибе. По­этому можно считать, что сжатие (растяжение) элементов продоль­ного набора крыла не сопровождается поперечными деформациями этих элементов и напряжения σ_х = 0.

Возможность рассматривать

Рис. 9.1. Напряжения и деформации крыло как безмоментную оболочку

крыла обусловлена тем, что местная жесткость

при изгибе отдельных его элементов весьма мала по сравнению с жесткостью при изгибе всего сечения.

Ниже излагается расчет сечения крыла от изгибающего момента, действующего в плоскости, перпендикулярной к плоскости хорд.

9.1.1. Исходные данные

Исходные данные: изгибающий момент М в сечении крыла, геометрические характеристики сечения (рис. 9.2) и характе­ристики жесткости элементов продольного набора. Последние задаются в виде зависимостей напряжений σ от деформаций ε (рис. 9.3). Различные элементы крыла обычно имеют неодинаковые и к тому же нелинейные зависимости σ от ε. Причиной этого может быть различие в материалах, из которых выполнены элементы конструкции, работа отдельных элементов за пределом пропорцио­нальности п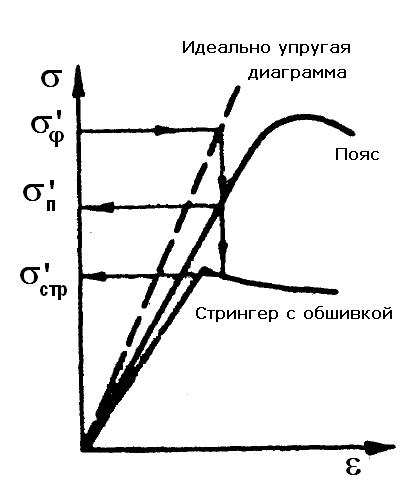 осле потери устойчивости.

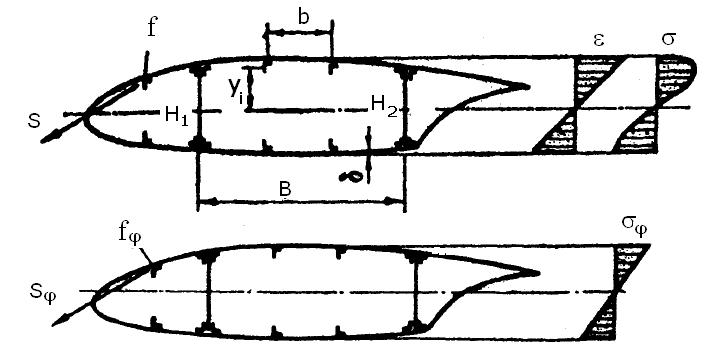
Рис. 9.2. Действительное (а) и редуцированное сечения (б) крыла. Рис. 9.3. Зависимости σ-ε для различных элементов крыла.