§3. Классификация задач оптимального управления
Большое разнообразие задач оптимального управления, встречающихся в различных сферах человеческой деятельности, порождает различные классы моделей (математических постановок) таких задач. Их можно группировать (классифицировать) по различным признакам.
С точки зрения условий протекания процесса управления отличают детерминированные и стохастические системы (см. рис. 1.3).
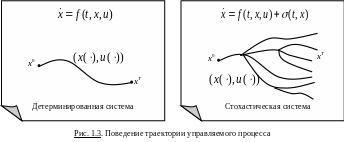
В детерминированных системах движение управляемого объекта при заданных начальных условиях вполне точно и однозначно определяется выбором положения "рулей" в каждый момент времени. При их изучении никакие случайности во внимание не принимаются.
В стохастических системах в процесс управления вмешиваются случайные факторы, действия которых могут быть оценены лишь с некоторой вероятностью (состояние погоды, поведение противодействующих сторон, сбой в работе механизмов управления и т.д.). Для учета действия случайных факторов в модели (1.1)-(1.5) вводятся соответствующие изменения: в уравнение движения добавляется "возмущающий" элемент, вместо траекторий и значений критерия качества рассматриваются их математические ожидания и т.д. Изучению всех этих вопросов посвящена самостоятельная теория оптимального управления стохастическими системами.
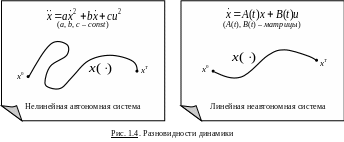
По характеру движения (по динамическим свойствам) различают (рис. 1.4):
нелинейные системы (f – нелинейная функция);
линейные системы (f – линейная функция);
неавтономные системы (f явно зависит от t);
автономные системы (f не зависит явно от t).
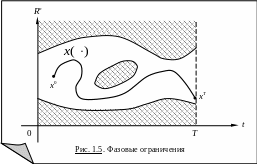
По характеру фазового пространства (в зависимости от наличия или отсутствия запрещенных состояний системы) различают задачи с фазовыми ограничениями и без таковых (рис. 1.5.).
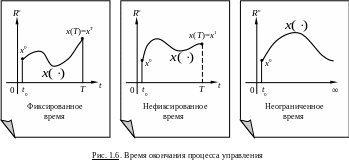
По протяженности во времени бывают задачи (см. рис. 1.6):
с фиксированным или нефиксированным временем окончания (
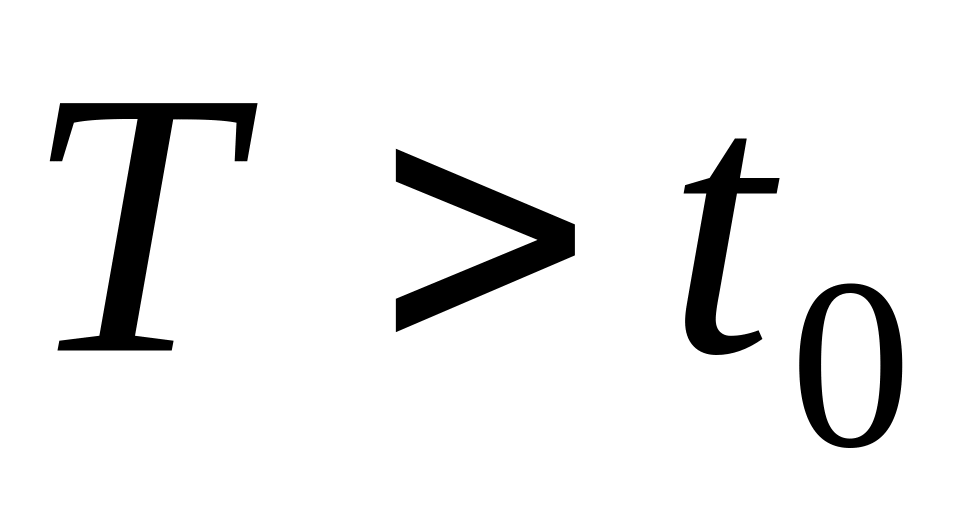);с неограниченной продолжительностью.
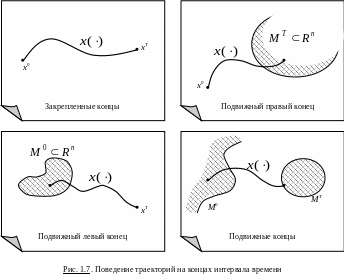
По характеру условий на концах траекторий различают задачи (см. рис. 1.7):
с закрепленными концами;
с подвижными левым или правым концами;
с подвижными концами.
По характеру оценки качества управления, т.е. по виду функционала качества бывают задача Больца, когда (см. (1.5))
;
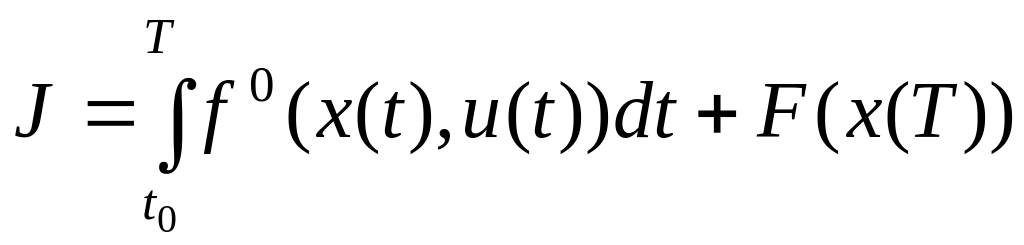задача Лагранжа, когда
;
задача Майера, когда
.
И, наконец, по характеру управления можно говорить о задачах программного или позиционного управления. Последнюю еще называют задачей синтеза оптимального управления. Подробному рассмотрению видов управлений посвящен следующий параграф.
§4. Классы допустимых управлений
Определение 1.1.
Любая функция
называется программным
управлением.
Программные
управления используют в тех практических
задачах, когда заранее принимается
решение (программа) о том, в какие моменты
времени
управление должно быть скорректировано.
В качестве примера такого управления можно привести процесс вывода искусственного спутника Земли на желаемую орбиту. Состояние спутника в каждый момент времени описывается высотой подъема, скоростью и массой, а в качестве управления выступает режим работы двигателя ракеты-носителя. Поскольку непосредственно и непрерывно управлять полетом не представляется целесообразным, заранее составляется программа полета, которая и выполняется автоматически во времени.
Другим примером может послужить работа станков с числовым программным управлением в том случае, когда обратная связь невозможна по технологическим причинам. Для них определяются оптимальные режимы (давление, температура, рабочие объемы и др.), чтобы общая эффективность работы была максимальной, а затем составляется программа, обеспечивающая работу станка во времени в соответствии с введенными начальными параметрами.
Программное управление, как функция одной переменной, является наиболее простым для формирования и потому сравнительно несложным для исследования с точки зрения оптимальности, существования и вычисления. В то же время оно имеет существенный недостаток – конструируется без учета текущих фазовых состояний системы.
Это наглядно можно продемонстрировать на примере отопительной системы, с температурой нагрева помещения в качестве фазовой переменной и расходом горючего в котельной в роли управления. Очевидно, что любая программа ее работы должна ориентироваться не только на время года, но и учитывать погодные условия: в случае потепления необходимо снизить расход топлива и уменьшить температуру, а при похолодании – увеличить подачу топлива.
Поэтому более практичными по сравнению с программными управлениями являются позиционные управления.
Определение 1.2.
Любая функция
(или
)
называется позиционным
управлением.
Задача нахождения позиционного
оптимального управления называется
задачей
синтеза.
Применение того или иного вида позиционного управления определяется исходя из содержания исследуемой задачи.
Естественно, что исследование задачи синтеза с точки зрения проблем управления сложнее, чем задачи программного управления.
Примером системы с позиционным управлением может служить движущийся автомобиль. Его состояние в каждый момент характеризуется пройденным расстоянием (или местоположением) и скоростью движения. Эти две величины меняются с течением времени, но не самопроизвольно, а сообразно воле водителя, который может по своему желанию управлять работой двигателя, увеличивая или уменьшая развиваемую этим двигателем силу, а также изменять направление движения, меняя угол поворота руля. При этом он может вовремя отреагировать на внештатную ситуацию и скорректировать процесс в зависимости от текущего положения и скорости (повернуть, начать торможение или ускориться).
В качестве другого
примера можно привести электрический
утюг с терморегулятором. Здесь фазовыми
координатами будут сила тока и температура
нагрева, а управляющим параметром –
положение регулятора. Чтобы избежать
порчи утюга и ткани, следует не допускать
перегрева и вовремя реагировать на
скачки напряжения в сети. Поэтому и
здесь целесообразным будет применение
позиционного управления. При этом в
математической постановке допускается
зависимость управления только от
текущего фазового состояния:
.
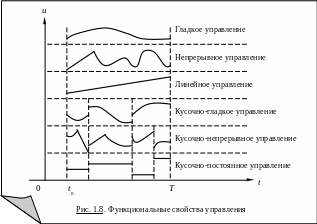
Класс допустимых управлений уточняется указанием их функциональных свойств по каждому аргументу, что также продиктовано содержанием рассматриваемой задачи. Такими свойствами управлений являются (рис. 1.8):
непрерывность, кусочная непрерывность, в частности, линейность, кусочное постоянство;
гладкость, кусочная гладкость;
измеримость.
Часто по разным аргументам управление имеет разные свойства. Например, позиционное управление может быть непрерывным по t и измеримым по x.
При исследовании практической задачи очень важно правильное определение адекватного содержанию задачи класса допустимых управлений. Например, исследование вопросов управления искусственным спутником Земли в классе гладких по t функций, кажущееся, на первый взгляд, заманчивым, скорее всего неверно, поскольку в этом классе управлений невозможно учитывать внештатные ситуации, требующие мгновенного переключения управления. Иначе говоря, в этой задаче среди гладких функций оптимального управления, скорее всего, нет, и нужно расширить класс допустимых управлений хотя бы до кусочно-гладких функций. Для точного ответа на этот вопрос перед математическим моделированием требуется доскональное изучение предметной области, дабы не получить псевдо-оптимального решения задачи.
Читателю предлагается самостоятельно проанализировать приведенные выше примеры с точки зрения определения для них подходящих функциональных свойств для допустимых управлений.