Раздел 1. Методологические основы теории оптимальных процессов

Раздел 1. Методологические основы теории оптимальных процессов

§1. Формализация задач оптимального управления

Теория оптимальных процессов – это наука, которая занимается математическими моделями управляемых объектов и систем с целью выработки оптимальных способов управления ими.

Управляемыми называются объекты или системы, на которые можно воздействовать извне при помощи каких-либо "рычагов" с целью изменения их состояния в желаемом направлении.

Рассмотрим некоторую управляемую систему (или объект), состояние которой в любой момент описывается n параметрами. Обозначим через x_i(t) значение i-го параметра в момент t, i = 1,…, n. Вектор x(t) = (x₁(t),…, x_n(t)) называется (фазовым) состоянием системы. Формально это есть точка n-мерного пространства Rⁿ, которое называется пространством состояний или фазовым пространством. Пусть объект снабжен m "рулями". Обозначим через u_j(t) значение j-го управляющего параметра в момент t (положение j-го руля в момент t). Вектор u(t) = (u₁(t),…, u_m(t)) называется управлением (в момент t), т.е. это есть вектор m-мерного пространства R^m.

Под воздействием управления u(t) изменяется состояние x(t), т.е. объект приходит в "движение". Процесс управления будем считать непрерывным, т.е. будем считать, что состояние объекта изменяется непрерывно во времени. Поэтому будем предполагать, что задан непрерывный отрезок времени [t₀,T]. Движение объекта будем рассматривать при непрерывном изменении времени t [t₀,T]. Для описания движения объекта применяется формула производной от функции времени x(t):

.

Для разных систем движение, т.е. значение , определяется по-разному.

Предположим, что известна функция f, описывающая скорость изменения состояния x(t) под воздействием управления u(t): f: Rⁿ ×R^m → Rⁿ или отображение

(x(t), u(t)) → f (x(t), u(t)).

Тогда мы можем написать:

t [t₀,T]. (1.1)

Это есть закон или уравнение движения (уравнение динамики) системы.

Под воздействием управления точка x(t), изменяясь во времени, описывает некоторую кривую в Rⁿ, которая называется траекторией движения. Для формального вычисления траектории надо интегрировать уравнение движения, а для этого нужно иметь начальные условия. Поэтому будем считать, что в начальный момент времени известно начальное состояние системы

. (1.2)

Система (1.1)-(1.2) составляет задачу Коши. Интегрируя ее, получаем описание траектории:

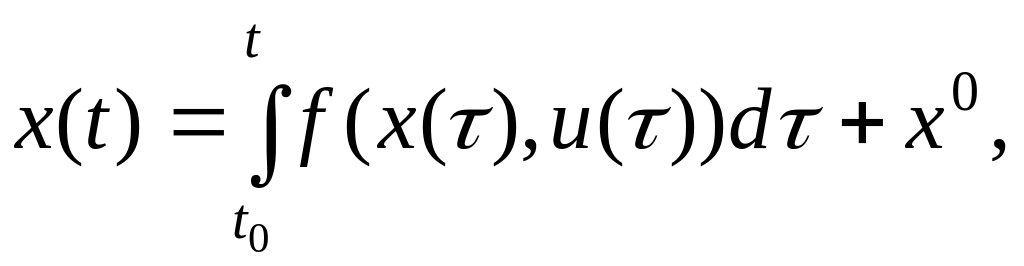t₀ ≤ t ≤ T.

Если траектория определена на всем отрезке t [t_0,T], ее будем обозначать так (рис. 1.1):

.

Точно так же для управления, определенного на всем отрезке времени [t_0,T], будем писать: , где u(t) – значение управления в момент времени t.

Для формализации реального факта ограниченности ресурсов управления будем считать заданным множество U  R^m такое, что в каждый момент времени t

u(t)  U  R^m. (1.3)

U называется множеством допустимых значений управляющих параметров. В самом простом случае U есть n-мерный параллелепипед:

или единичный круг:

.

Любая функция u, определенная на всем отрезке времени [t_0,T] и в каждый момент t [t₀,T] принимающая значение из заданного множества U, называется допустимым управлением: u: [t₀,T] → U.

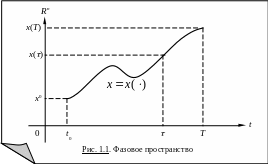
Таким образом, любой управляющий параметр u(t) – постоянный вектор (мгновенное значение управления в момент t), а управление – это функция на [t₀,T] (рис. 1.2).

Множество всех допустимых управлений обозначим через U. Подчеркнем: U – множество точек, U – множество функций. В зависимости от рассматриваемой конкретной задачи допустимые управления могут иметь различные функциональные свойства (непрерывность, кусочная непрерывность, гладкость, измеримость и т.д.).

Пусть задано фазовое состояние x^T Rⁿ, в которое требуется привести систему в конечный момент T (цель управления), т.е. должно выполняться условие

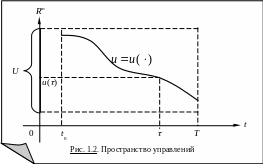
x(T) = x^T. (1.4)

В дальнейшем будем предполагать, что для любого допустимого управления существует и единственна соответствующая ему траектория системы (1.1)-(1.2).

С помощью соотношений (1.1)-(1.4) может быть сформулирована задача управления: требуется найти такое допустимое управление , которое приводит систему (в силу уравнения (1.1)) из заданного начального состояния x⁰ в предписанное конечное состояние x^T.

Оказывается, что задача управления почти всегда разрешима и часто существует множество допустимых управлений, решающих эту задачу. Поэтому имеет смысл ставить более сложную оптимизационную задачу – задачу о наилучшем (в том или ином смысле) решении задачи управления. Другими словами, из всех управлений, решающих задачу управления, нужно найти то, которое соответствует, например, кратчайшему расстоянию, быстрейшему достижению точки, наименьшему расходу ресурсов, наименьшему риску и т.д.

Для формализации этого вопроса задается функционал качества, определенный на множестве всех траекторий системы (1.1)-(1.2). Этот функционал в общем случае имеет вид

, (1.5)

где функция f  ⁰ оценивает мгновенный процесс (x(t), u(t)), а F – качество достижения конечной точки x(T). Первое слагаемое в (1.5) называется интегральной частью, а второе – терминальной. Функционал (1.5) каждой паре или соответствующей ей траектории ставит в соответствие число, оценивающее качество этой траектории.

Соотношения (1.1)-(1.5) образуют задачу оптимального управления, в которой требуется найти допустимое управление , переводящее систему из заданного начального состояния x⁰ в предписанное конечное состояние x^T так, чтобы вдоль соответствующей ему траектории функционал качества (1.5) принимал максимальное (минимальное) значение.

Другими словами, из числа всех допустимых управлений, решающих задачу управления, требуется найти то, которое максимизирует (минимизирует) функционал (1.5).

Управление, решающее эту задачу, называется оптимальным управлением, соответствующая ему траектория – оптимальной траекторией, а пара – оптимальным процессом.

Основными вопросами исследования в задачах оптимального управления являются:

– нахождение условий существования оптимальных управлений в различных классах допустимых управлений;

– нахождение необходимых и достаточных признаков оптимальности управлений;

– разработка методов вычисления оптимальных управлений.