4. Схемы створных измерений (полного створа, последовательных створов, частных створов, частей створа, последовательных створов по частям).

Программа общего створа (рис.1,а), когда нестворности всех точек определяются относительно общего створа между концевыми (опорными) пунктами створа.

Программа общего створа реализуется в двух вариантах:

1. в створе двух крайних пунктов последовательно определяют нестворности всех промежуточных точек непосредственным (сквозным) визированием;

2. в створе двух крайних пунктов определяют нестворности промежуточных пунктов, начиная с середины на себя; затем, меняя местами створный прибор и ориентируя визирную цель, также определяют нестворности точек, расположенных во второй части створа; для контроля средняя точка определяется дважды с обоих опорных пунктов створа.

Во втором варианте средняя точка определяется с такой же точностью, что и в первом. Нестворности остальных промежуточных точек получаются с более высокой точностью. Однако второй вариант имеет существенный недостаток.

Из-за отсут­ствия обратного хода в нем не исключаются систематические по­грешности (инструментальные, личные и т. п.).

По программе частных (пересекающихся) створов (рис.1,б) прибор ориентируют относительно всего створа при определении первой промежуточной точки, а нестворности остальных измеряют от створов предыдущей и последующей точек створа: например, частную нестворность второй точки оп­ределяют от створа 1—3, третьей – от створа 2—4 и так далее. Однако из-за влияния внешних условий и сложившейся строительно-монтажной обстановки визирование на конечную точку может оказаться нецелесообразным. В этом случае можно использовать оптический метод визирования по программе рав­ных частных створов. Для измерений по этой программе створ I—II разбивают на равные части и в створе I—2 определяют частную нестворность точки 1. Затем инструмент переносят в точку 1 и в створе 1—3 определяют частную нестворность, точки 2 и так далее до створа (п—1)—II. Величина нестворности 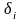i-й промежуточной точки является функцией измеренных частных нестворностей относительно каждого из частных створов, т. е. , и может быть получена из следующей системы уравнений:

; ;

; ,

где п — число определяемых пунктов створа; i — номер пункта, нестворность которого вычисляется;

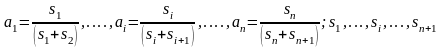– длины частных створов.

Если створ длиной L разделить на п+1 равных частей, то решение системы уравнений (8.7) для i-того пункта примет вид:

.

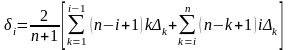Приняв точность измеренных частных нестворностей одинаковой, получим формулу для вычисления средней квадратической погрешности определения искомой нестворности

, (8.9)

где k — номер частного створа.

Из изложенного следует, что при одной и той же длине створа погрешность определения средней точки меньше, когда створ разделен на меньшее число частей.

Преимущества программы равных частных створов заклю­чаются в следующем:

• она позволяет выполнять измерения даже при неблагоприят­ных внешних условиях, когда просматривается лишь несколько точек створа;

• с большей точностью определяется взаимное положение смежных пунктов, что в ряде случаев является наиболее важ­ным, например, при установке оборудования ускорителей;

• практически полностью исключаются погрешности за перефокусировку для средних значений нестворностей, полученных из прямого и обратного ходов.

Программа последовательных створов (рис.1, в). Частную нестворность пункта 1 определяют относительно створа I—II, затем относительно частного створа 1 — II измеряют и так далее до последнего частного створа (п -1)— II, относительно которого определяют 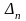точки п. Затем аналогично измерения производят в обратном направлении.

Искомые нестворности по измеренным частным нестворностям можно получить из решения следующих уравнений по правилу Крамера:

; ; ;

; .

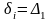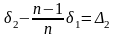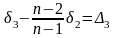Формула для вычисления искомых нестворностей по измеренным частным нестворностям может быть записана сокращенно в виде

.

В общем случае при неравномерном расположении промежуточных точек вдоль створа искомые нестворности вычисляют по следующим формулам: для прямого хода

; ;

;

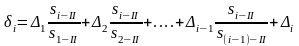для обратного хода: ; ;

,

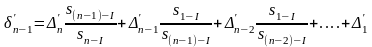где Si-II, Si-I—длины отдельных последовательных створов при измерениях в прямом и обратном направлениях соответственно; п — число определяемых промежуточных пунктов створа.

Обозначив n+1=2q и приняв i=q, получим формулу для вычисления нестворности 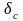средней точки по измеренным частным нестворностям

.

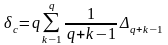Можно считать, что в рассматриваемой программе средняя точка является наиболее слабой по точности. Приняв точность измерения частных нестворностей одинаковой , получим формулы для расчета средних квадратических погрешностей искомых нестворностей любых и средней точек створа ; ;

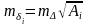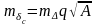где

Анализ формулы (8.15) показывает, что при q>5 средняя квадратическая погрешность в середине створа может быть подсчитана по приближенной формуле

.

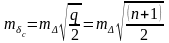Расчеты показывают, что чем длиннее створ, тем эффективнее применять эту программу при сохранении одной и той же длины шага. Отсюда можно сделать важный практический вывод: чем больше длина створа, тем меньше относительная погрешность 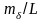створных измерений при одной и той же длине шага.

Программа последовательных створов по частям (рис.1,г). В определенных условиях целесообразно применять программу измерений, выгодно сочетающую преимущества программ последовательных створов и равных частных створов.

Пусть створ I—II разбит на три части с узло­выми пунктами I^’ и II' и промежуточными пунктами 1, 2, . . . 9. Сущность рассматриваемой программы заключается в следующем:

1) в створе I – II' определяется точка 1, затем в створе 1–II' определяется точка 2, в створе 2—II^’ – точка 3;

2)затем в створе I'—II определяется точка 5, в створе 5—II — точка 6 и так далее все точки (7,..., 12), т. е. ориентирование зрительной трубы производится на ²/з общей длины створа;

3) дополнительно определяется нестворность точки I' относительно полного створа I – II.

Приведение узловых точек I' и II' соответственно к створам I—II' и I'—II выполняется по формуле (8.11). Нестворности этих точек относительно общего створа I—II вычисляют по формуле (8.8). Анализ результатов измерений, выполненных по программе последовательных створов по частям, позволяет отметить следующее: чем меньше узловых точек I', II', тем ближе по точности эта программа к программе последовательных створов, и чем больше узловых точек, тем ближе к программе равных частных створов. Следует обратить внимание на значительную разницу величины 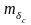, полученной по программе последовательных и равных частных створов. Это связано с закономерностями накопле­ния погрешностей измерений. Чтобы в определенной степени сгладить кривую роста погрешностей, при измерении по программе равных частных створов следует стремиться дополнительно измерить полную нестворность первой и последней (n-й) промежуточных точек. Эти два избыточных измерения позво­ляют подсчитать угловую и координатную невязки и произвести уравнивание результатов измерений. После уравнивания конеч­ные результаты оказываются более близкими к полученным по программе последовательных створов.

Таким образом, приведенный анализ основных программ створных измерений методами оптического визирования позво­ляет сделать следующие основные выводы:

• наиболее точные результаты обеспечивает программа последовательных створов коротким визирным лучом;

• если створ разбит на части, то оптимальной является программа последовательных створов по частям, когда в створе ми­нимальное число частей (три части), а все основные и проме­жуточные точки определяются по программе последовательных створов с ориентированием зрительной трубы на (²/з) L
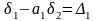