3.2 Завдання

3.2.1 Сигнал є періодичною послідовністю імпульсів прямокутної форми з амплітудою А, тривалістю і періодом повторення Т (рис. 3.1). Аналітичний опис функції має вигляд:

,

де x =  t;  =  / Т.

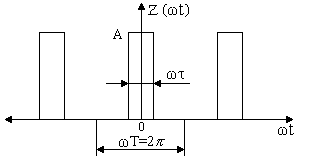
Рисунок 3.1 – Імпульси прямокутної форми

Обчисліть лінійчасті спектри при А = 1 та  = 0,05; 0,1. Число гармонік N прийняти рівним 20.

Побудуйте лінійчастий спектр періодичної послідовності прямокутних імпульсів , відклавши по осі абсцис (номери гармонік).

За результатами розрахунків зробіть висновки щодо:

• пелюсткового характеру огинаючої спектра послідовності прямокутних імпульсів;

• відсутності чи присутності в спектрі гармонік з номерами, кратними щілинності послідовності імпульсів ;

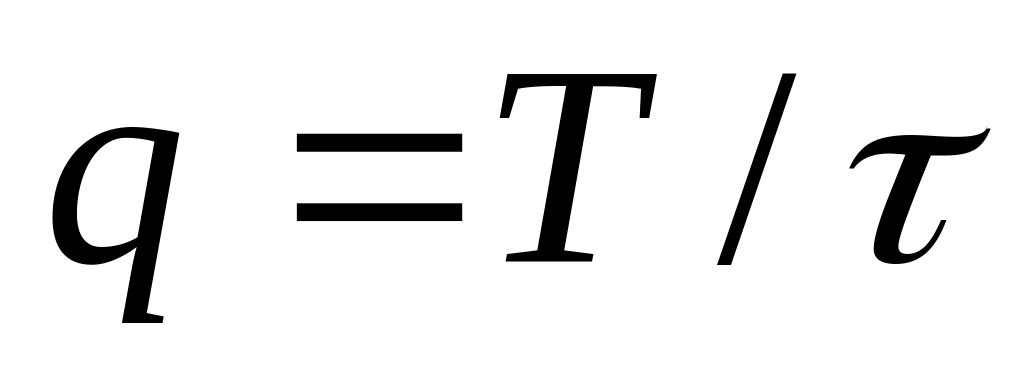• тенденції змінення рівня спектральних складових та ширини основного пелюстка при збільшенні періоду Т удвічі;

• наявності прямої чи зворотної залежності між тривалістю сигналу та шириною його спектра;

• відстані за частотою між сусідніми гармоніками (дорівнює вона чи ні частоті проходження імпульсів).

Зауваження: спектральні складові заданої функції можна обчислити також за формулою:

.

Вказівка: функція парна, тому синусні складові (формула 3.1) в розкладанні дорівнюють нулю.

3.2.2 Сигнал описується періодичною функцією, що складається з імпульсів косинусоїдальної форми. Функція на ділянці описується формулою:

,

де .

Задано нижній кут відсікання, який може виражатися в градусах (позначається як UG) і в радіанах (позначається як U), причому U=UG/180. При розрахунку прийняти, що UG = 60⁰, А = 1.

Побудуйте графік залежності в інтервалі зміни аргументу х від мінус π до плюс π.

Розрахуйте постійну складову a₀/2 і амплітуди гармонік a_n при n=115, а також їхні значення, виражені в децибелах відносно першої гармоніки сигналу:

.

Побудуйте амплітудно-частотний спектр періодичної функції , відклавши на осі абсцис відношення (інтервал зміни відношення прийняти рівним від 0 до 15).

Вказівки: 1) функція Ф( t) парна, тому синусні складові (формула 3.1) в розкладанні дорівнюють нулю;

2) період функції дорівнює ;

3) програма розрахунку спектра заданої функції наведена у Додатку А.

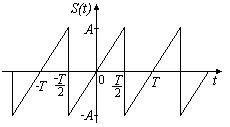3.2.3 Сигнал S(t) є періодичною послідовністю трикутних імпульсів (рис. 3.2).

Рисунок 3.2 – Пилкоподібний сигнал

В межах періоду він описується функцією:

.

Сигнал S(t) є парною функцією, тому в його спектрі присутні тільки косинусні складові:

.

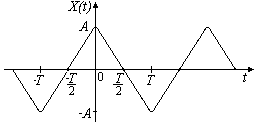Сигнал X(t) є періодичною послідовністю трикутних імпульсів (рис.3.3).

Рисунок 3.3 – Послідовність трикутних імпульсів

В межах періоду він описується функцією:

.

Сигнал X(t) є непарною функцією, тому в його спектрі присутні тільки синусні складові:

.

Побудуйте спектри сигналів S(t) та X(t). Порівняйте швидкості спадання спектрів вказаних сигналів. Зробіть висновок щодо залежності швидкості спадання спектра від ступеня гладкості сигналу.