Методические указания по 3, 4 лабароторным работам

МИНИСТЕРСТВО НАУКИ, ВЫСШЕЙ ШКОЛЫ И ТЕХНИЧЕСКОЙ ПОЛИТИКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Московский Государственный Институт Электроники и Математики

(технический университет)

Кафедра автоматики и управления

в технических системах

ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК РАЗОМКНУТОЙ И ЗАМКНУТОЙ САР, ЧАСТОТНЫХ ПОКАЗАТЕЛЕЙ КАЧЕСТВА И

ОЦЕНКА УСТОЙЧИВОСТИ САР

ЧАСТОТНЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ САР

Частотными характеристиками обыкновенной линейной САР (рис.1) называется Формулы и графики, характеризующие реакцию системы на гармоническое входное воздействие в установившемся режиме.

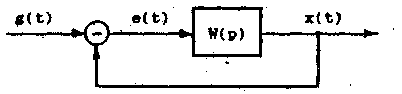
Рис. 1.

Гармоническое входное воздействие - это Функция времени, которая может быть представлена в виде линейных комбинаций Функций sin(wt) и cos(wt). Если на вход системы подать гармоническое воздействие

g(t)=x1(t)=X1m*cos(wt) , (1)

где Х1m - амплитуда воздействия; w - угловая частота воздействия, то на выходе системы в установившемся режиме будет также гармони­ческая функция той же частоты w, но в общем случае сдвинутая по фазе относительно входной величины на угол Ч, т.е.

x(t)=x2(t)=X2m*сos(wt+Ч) , (2)

где Х2m - амплитуда выходной величины; Ч - сдвиг фаз между выходной и входной величинами. Одной из важнейших характеристик разомкнутой САР является ее частотная передаточная функция (ЧПФ) W(jw). которая легко подучается из обычной передаточной функции разомкнутой системы W(p) подстановкой р=jw. Она представляет собой комплексное число, модуль А(w) которого равен отношению амплитуды выходной величины Х2м и амплитуде входной величины Х1м, а аргумент Ч(w) - сдвигу Фаз выходной величины по отношению к входной

A(w)=mod W(jw) = |W(jw)|=X2m/Xlm , (3)

Ч(w)=arg W(jw) (4)

ЧПФ W(jw) может быть представлена в виде:(5)

где U(w) и V(w) - вещественная и мнимая составляющие ЧПФ. Для нахождения зависимостей А(w), Ч(w), U(w), V(w) исполь­зуются следующие Формулы :

Для наглядного представления частотных свойств САР ис­пользуются следующие частотные характеристики . 1) Амплитудно-фазовая частотная характеристика (АФЧX) W(jw) -это кривая, описываемая концом вектора W(jw) на комплексной плоскости U-V (годограф вектора W(jw)) при изменении частоты входного воздействия w от -оо до + оо (рис.2). Длина вектора, проведенного из начала координат в точку АФЧК, соответствующую какой-либо выбранной частоте w*, равна модулю A(w*) ЧПФ.

Угол между этим вектором и положительным направлением вещест­венной оси равен аргументу или Фазе Ч(w*) ЧПФ. АФЧХ соответствует выражение (5).

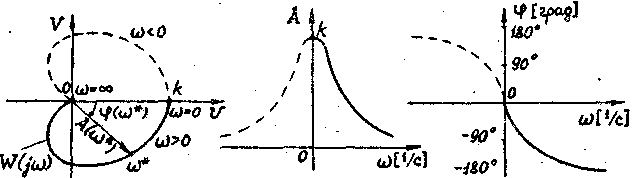
Рис. 2. Рис..3. Рис. 4.

2. амплитудная частотная характеристика (ЯЧХ) А(w) - это кривая изменения отношения амплитуд выходной и входной величин в зави­симости от частоты w (рис.3). Она показывает, как пропускает САР сигнал различной частоты. АЧХ соответствует выражение (8).

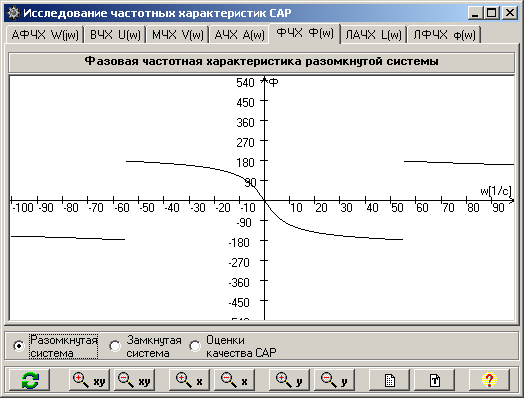
3. Фазовая частотная характеристика (ФЧХ)Ч(w) - это кривая изме­нения сдвига фаз выходной величины по отношению к входной в зависимости от частоты w (рис.4). Она показывает фазовые сдвиги, вно­симые САР на различных частотах. ФЧХ соответствует выражение (9).

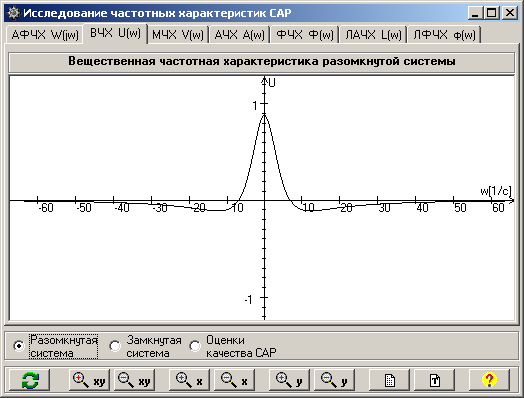
4. Вещественная частотная характеристика (ВЧК) U(w) - это кривая, которой соответствует вещественная составляющая ЧПФ (рис.5) и вы­ражение (6).

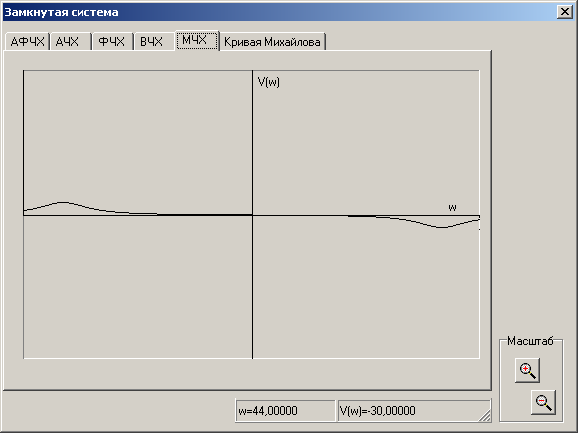
5. Мнимая частотная характеристика (МЧХ) V(w) - это кривая, которой соответствует мнимая составляющая ЧПФ (рис.6) и выражение (7).

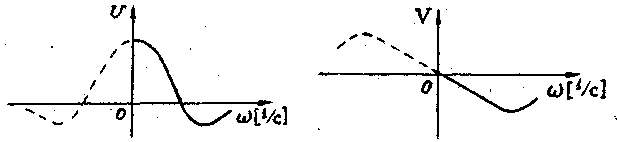
Рис. 5. Рис. 6.

Кривые АФЧХ, АЧХ, #ЧХ, ВЧХ, МЧХ обладают свойством симметрии, поэтому по результатам вычисления кривых для положительных част >т можно построить кривые для всего диапазона частот –оо<w< + оо , так как U(-w)=U(w), V(-w)=-V(w), А(-w)=А(w), Ч(-w)=-Ч(w).

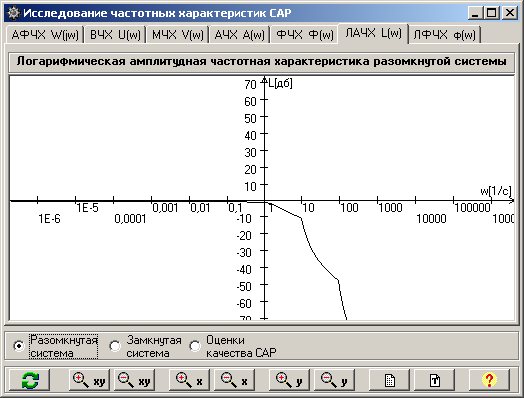
6) Логарифмическая амплитудная частотная характеристика (ЛАЧХ) L(w) - это кривая (рис.7), построенная в логарифмическом масштабе частот в соответствии с выражением

L(w)=20*lg[A(w)] (10)

Единицей измерения величины L(w), которая откладывается по оси ординат, является децибел. По оси абсцисс откладывается частота w [1/с] в логарифмическом масштабе. Равномерной единицей на оси абсцисс является декада – это любой отрезок, на котором значение частоты увеличивается в 10 раз.

Рис. 7.

Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза Wc. Она определяется из условия

L(w)=0 или A(w)=l (11)

Ось абсцисс (L(w)=0) соответствует значению A(w)=l, т.е. про­хождению амплитуды сигнала через САР без изменения. Верхняя полуплоскость ЛАЧХ соответствует значениям А(w)>1, т.е. усиле­нию амплитуды, а нижняя полуплоскость - значениям A(w)<l, т.е. ослаблению амплитуды. ЛАЧХ может быть приближенно построена в виде асимптотической ЛАЧХ, представляющей собой совокупность отрезков прямых линий (асимптот) с наклонами, кратными величи­не 20 дб/дек.

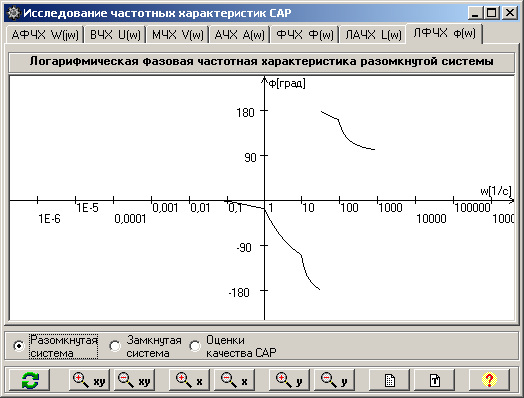
7) Логарифмическая Фазовая частотная характеристика (ЛФЧХ) - это кривая ФЧХ Ч(w), построенная в логарифмическом масштабе частот (рис.8). По оси ординат откладывается частота w [l/c] в логарифмическом масштабе, как при построении ЛАЧХ.

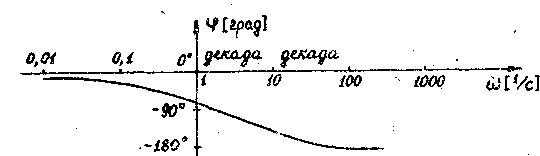
Рис. 8,

Для исследования замкнутой системы с передаточной Функцией Ф(Р) = W(р)/[1+W(p)] (12)

используются понятия, формулы и характеристики, аналогичные , тем, что рассмотрены выше для разомкнутой системы.

Частотными называются оценки качества, позволяющие по виду частотных характеристик разомкнутой и замкнутой САР количественно оценить запас устойчивости и быстродействие системы.

Величина запаса устойчивости показывает, насколько далеко находится САР от колебательной границы устойчивости, за которой в системе возникают незатухающие автоколебания. Под быстродействием САР понимается быстрота реагирования САР на появление управляющих и возмущающих воздействий.

К числу основных частотных оценок качества САР относятся :

1. запас устойчивости по амплитуде (или по модулю) h (в линейном масштабе) и l (в логарифмическом масштабе);

2. запас устойчивости по фазе Y;

3. показатель колебательности Ммах;

4. резонансная частота Wp; Б) частота среза Wc;

6) частота Wп, соответствующая полосе пропускания замкнутой системы.

З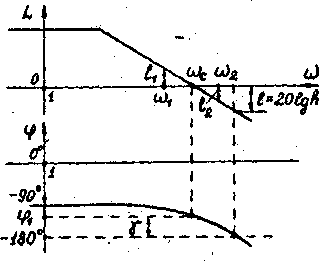апасом Устойчивости по амплитуде h называют минимальный от­резок действительной оси, характеризующий расстояние между крити­ческой точкой (-1,jO) и ближайшей к ней точкой пересечения кривой АФЧХ разомкнутой системы W(jw) с действительной осью (рис.9).

Запасом устойчивости по Фазе Y называют минимальный угол, образуемый радиусом, проходящим через точку пересечения кривой AФЧХ разомкнутой системы W(jw) с окружностью единичного радиуса с центром в начале координат, и отрицательной частью действительной оси (рис.9).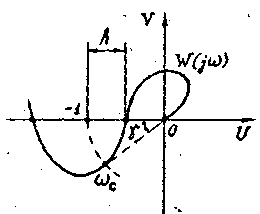

Рис. 9. Рис. 10.

На рис.10. показано, как по логарифмическим частотным характерис­тикам разомкнутой системы можно найти запас устойчивости по амп­литуде, выраженный в децибелах

l=20*lg(h) (13)

и запас устойчивости по фазе

у=180°+Ч1 (14)

где Ч1 - значение ФЧХ разомкнутой системы при частоте среза Wс, соответствующее модулю, равному единице

Лабораторная работа №3 – Исследование частотных характеристик САР

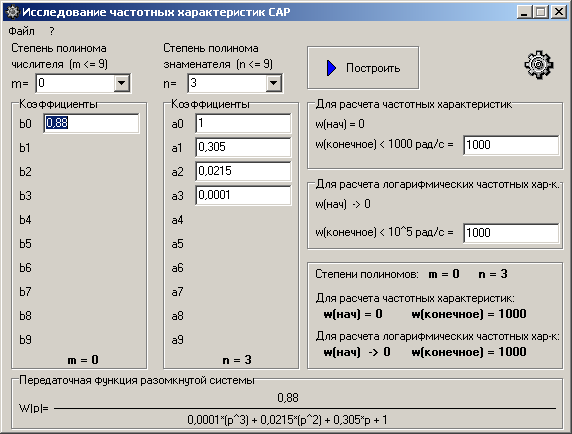
Быстродействие САР количественно характеризуется следующими оценками качества, определяемыми по АЧХ замкнутой системы при начальной ординате, равной единице (рис.12):

1) Wp - резонансная частота, соответствующая резонансному пику

АЧХ;

2) Wс- частота среза, соответствующая условию

A(Wc)=l (19)

3) Wп - частота, соответствующая полосе пропускания замкнутой

системы и определяемая из условия

A(Wп)=1/ V2=0,707 , (20)

где использовано обозначение A(w)=|Ф(jw)|.

Допустимые значения этих характерных частот, как и соответ­ствующая им допустимая длительность переходного процесса tпп, могут сильно меняться в зависимости от типа и назначения САР,

Понятие устойчивости САР связано со способностью системы возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

Оценка устойчивости САР производится по алгебраическим или частотным критериям устойчивости, описанным в [1,2,3]. К частотным критериям устойчивости относятся :

1. критерий устойчивости Михайлова ;

2. критерий устойчивости Найквиста ;

3. оценка устойчивости САР по ее ЛЧХ. Если в характеристический полином замкнутой САР(21)

где R(р), Q(p) - полиномы числителя и знаменателя передаточной Функции разомкнутой системы W(p)=R(p)/Q(p) , подставить значение p=jw, то получим характеристический комплекс (22)

г де его вещественная X(w) и мнимая Y(w) части определяются как (24,25)

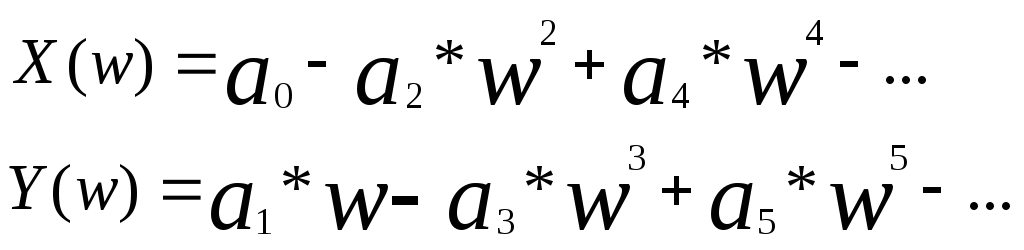
а функции D(w) и Ф(w) представляют собой модуль и аргумент (фазу) характеристического комплекса D(jw),

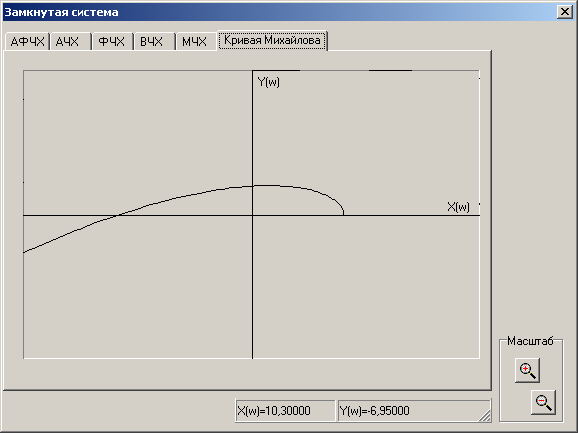
При изменении частоты w от 0 до  вектор D(jw) из комплексной плоскости X-Y опишет своим концом кривую (годограф вектора D(jw)), называемую кривой Михайлова (рис. 14).

Рис. 14.

Критерий устойчивости Михайлова формулируется таким образом :

- для устойчивости линейной САР n-го порядка необходимо и достаточно, чтобы кривая Михайлова при изменении частоты w от 0 до бесконечности проходила последовательно n квадрантов в направлении против часовой стрелки, окружая начало координат, причем ее конец должен уходить в бесконечность в том квадранте комплексной плоскости X-Y, номер которого равен степени характеристического уравнения n.

Критерий устойчивости Найквиста в общем случав формулируется следующим образом :

- для устойчивости замкнутой САР необходимо и достаточно, чтобы разность между числами положительных (сверху вниз) н отрицательных (снизу вверх) переходов AФЧХ разомкнутой системы W(jw) через ось абсцисс левее точки (-1,j0) при изменении частоты и от

Рис. 17.

0 до  была равна к/2, где k - число корней характеристического уравнения разомкнутой системы с положительной вещественной частью. При этом начальная точка характеристики на оси абсцисс левее точки (-1,j0) считается как половина перехода. Для систем, находящихся в разомкнутом состоянии на границе устойчивости, т.е. имеющих  ну­левых корней характеристического уравнения, число k считается рав­ным нулю, а АФЧX W(jw) берется с дополнением в бесконечности (рис. 15, 16, 17).

На основании критерия устойчивости Найквиста могут быть

сформулированы требования, которым должны удовлетворять логариф­мические частотные .характеристики разомкнутой системы для того, чтобы она была устойчива в замкнутом состоянии. Это связано с тем,

что в точках пересечения АФЧХ W(jw) отрезка (- оо ,-1) ЛАЧХ L(w)

положительна, а ЛФЧХ Ч(w) пересекает прямую (-180°) снизу вверх

(положительный перевод) или сверху вниз (отрицательный переход). Требования к ЛАЧХ и ЛФЧХ в общем случае формулируются следующим образом:

Рис. 18.

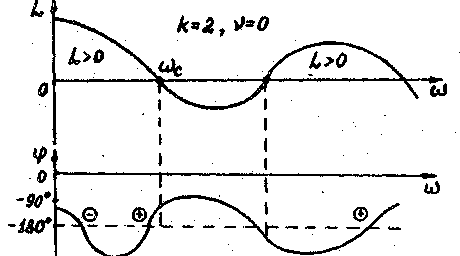- для устойчивости замкнутой САР необходимо и достаточно, чтобы разность между числами положительных и отрицательных пере­ходов ЛФЧХ Ч(w) разомкнутой системы через прямую

(-180°) при тех значениях частоты w, для которых ЛАЧХ L(w) разомкнутой системы положительна, была равна k/2, где k - число корней характеристи­ческого уравнения разомкнутой системы с положительной вещественной частью. При этом начало ЛФЧХ в бесконечно удаленной точке w=0 на прямой (-180°) считается за половину перехода. В случае астати­ческих систем (#0) при подсчете точек пересечения ЛФЧХ с прямой (-180°) надо иметь в виду, что если начало ЛФЧХ лежит ниже прямой (-180^е) (что соответствует АФЧХ на рис,16), то в число отрицатель­ных переходов надо включать бесконечно удаленную влево точку w=0.(рис 18)

Лабораторная работа №4 – Исследование частотных характеристик разомкнутой и замкнутой САР, оценка качества и устойчевости САР