28) Диаграммы фазового равновесия. Основные принципы в методе физико-химического анализа диаграмм состояния.

Однокомпонентной системой является любое простое вещество или химическое соединение, обладающее строго определенным составом в газообразном, жидком и твердом состояниях. Диаграмму состояния обычно строят на плоскости в координатах T-p . Фазовые поля (области существования) пара V, жидкости L и твердой фазы Sдивариантны, т.е. допускают одновременное изменение двух параметров состояния - Т и р.

 S, L и V - соответственно области существования твердой, жидкой и паровой фаз; 1, 2 и 3 - кривые кипения (испарения), плавления и возгонки (сублимации) соответственно, К - критическая точка; А - тройная точка. 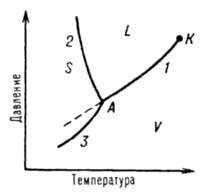Двухфазное равновесие между жидкостью и паром изображается кривой кипения (или испарения) 1, между жидкостью и кристаллами - кривой плавления 2, между кристаллами и паром - кривой возгонки (или сублимации) 3. Все двухфазные равновесия моновариантны, т.е. не нарушаются при произвольном изменении только одного из параметров, Т или р; при этом значение другого определяется из диаграммы состояния. Кривая кипения 1характеризует зависимость давления насыщенного пара вещества от температуры или зависимость температурыкипения вещества от внешнего давления. Со стороны повышенных T и р эта кривая заканчивается в критической точкеК, где исчезает различие в свойствах между жидкостью и ее паром (подробнее см. ст. Критическое состояние). Жидкость может находиться в переохлажденном состоянии (пунктирная линия на рис. 1). Аналогично криваяплавления характеризует зависимость температуры плавления от внешнего давления, кривая возгонки - температурную зависимость давления насыщенного пара над твердым веществом. На рис. 1 ход кривой плавления соответствует повышению температуры плавления с ростом давления, однако возможно и понижение температуры плавления с давлением. Все три кривые моновариантных фазовых равновесий сходятся втройной точке А, отвечающей параметрам состояния, при которых находятся в нонвариантном равновесии три фазы.Диаграмма состояния усложняется, если вещество в твердом состоянии может существовать в различных кристаллических модификациях. Каждой модификации отвечает свое фазовое поле. Линии моновариантных равновесий, разграничивающие эти поля, называют кривыми превращений.

29) Гетерогенное равновесие. Бинарные системы. Законы Рауля. Законы Коновалова.

30) Вид и анализ простой диаграммы кипения и диаграммы кипения с образованием азиотропной смеси.

31) Вид и анализ диаграмм состояния двухкомпонентных систем температура-состав для жидкостей и ограниченной растворимостью.

32) Вид и анализ диаграммы кипения для жидкостей с ограниченной растворимостью.

33) Основы фракционной перегонки

34) Теоретическое построение диаграмм плавкости. Уравнение Шредера и его анализ.

35)Сущность термического анализа и кривые охлаждения. Вид и анализ диаграммы плавкости двухкомпонентных систем без образования хим. соединения.

36)Вид и анализ даограмм плавкости двухкомпонентных систем с образованием устойчивых химических соединений.

37). Вид и анализ диаграмм плавкости двухкомпонентных систем с образованием неустойчивых химических соединений.

Билет№2

1)I начало термодинамики его формулировки:

в любой изолированной системе запас энергии остается постоянным;

разные формы энергии переходят друг в друга в строго эквивалентных количествах;

вечный двигатель первого рода невозможен; такой двигатель который производил бы работу, не затрачивая на это энергии.

внутренняя энергия является функцией состояния, т.е. её изменение не зависит от пути процесса, а зависит только от начального и конечного состояния системы.

аналитическое выражение: Q = DU +W ; для бесконечно малого изменения величин dQ = dU + dW.

1-ое начало термодинамики устанавливает соотнош. м/у теплотой Q, работой А и изменением внутр. энергии системы ΔU. Изменение внутр. энергии системы равно кол-ву сообщенной системе теплоты минус кол-во работы, совершенной системой против внешних сил.

- математическая запись 1-го начала термодинамики.

Изохорный процесс (V = const; ΔV = 0).

Поскольку работа расширения равна произведению давления и изменения объема, для изохорного процесса получаем:

; ; ;Следовательно при const=V вся теплота подведенная к системе расходуется на увеличение внутренней энергии или все изменение внутренней энергии обращается в теплоту.

Изобарный процесс (Р = const).

;

Подставляя полученные выражения в ; ; ; (I.7)

В уравнении (I.7) сгруппируем переменные с одинаковыми индексами. Получаем:

(I.8)

Введем новую функцию состояния системы – энтальпию H, тождественно равную сумме внутренней энергии и произведения давления на объем:

Тогда выражение (I.8) преобразуется к следующему виду: (I.9)

Т.о., тепловой эффект изобарного процесса равен изменению энтальпии системы.

Изотермический процес( T=const)

U=f(T) cледовательно dU=0, SQ=dU+pdV следует dQt=pdv=dWmax. Таким образом для изотермического процесса теплота подведенная к системе расходуется на совершение работы системой.

Адиабатический процес (Q=0) Процесс без теплообмена SQ=dU+pdV cлед 0=dU+pdV; -dU=pdV=SWmax. Работа преобретает св-ва функции состояния в адиабатических условиях совершает работу за счет убыли внутр энергии.

2) По свойствам веществ, участвующих в потенциалопределяющих процессах, принята след. классификация электродов: электроды 1-ого и 2-ого рода, газовые, окислительно-восстановительные и ионообменные. Электроды 1-ого рода: металлические в том числе и амальгамные, металлоидные. Газовые (относятся к электродам 1-ого рода): водородный, кислородный. Электроды 2-ого рода (состоят из 3-х фаз):каломельный,хлосеребряный.Окислительно-восстановительные электроды.Ионообменные электроды или ионоселективные: например, стеклянные электрод.Электродами второго рода являются электроды, в которых металл покрыт малорастворимой солью этого металла и находится в растворе, содержащем другую растворимую соль с тем же анионом. Электроды этого типа обратимы относительно аниона и зависимость их электродного потенциала от температуры и концентрации аниона может быть записана в следующем виде:

В случае окислительно-восстановительных электродов процессы получения и отдачи электронов атомами или ионами происходят не на поверхности электрода, а только в растворе электролита. Если опустить платиновый (или другой инертный) электрод в раствор, содержащий двух- и трехзарядные ионы железа и соединить этот электрод проводником с другим электродом, то возможно либо восстановление ионов Fe³⁺ до Fe²⁺ за счет электронов, полученных от платины, либо окисление ионов Fe²⁺ до Fe³⁺ с передачей электронов платине. Сама платина в электродном процессе не участвуют, являясь лишь переносчиком электронов. Такой электрод, состоящий из инертного проводника первого рода, помещенного в раствор электролита, содержащего один элемент в различных степенях окисления,  называется окислительно-восстановительным

Потенциал окислительно-восстановительного электрода также определяют относительно стандартного водородного электрода: Pt, H₂/ 2H⁺// Fe³⁺, Fe²⁺/ Pt.

Билет№4

1)Теплоемкостью называют количество теплоты, которое необходимо сообщить системе для её нагревания на 1 К в условиях отсутствия полезной работы. Различают удельную и молярную теплоемкости. Удельная- количество теплоты, необходимое для нагревания единицы массы вещества на 1К Молярная- количество теплоты, необходимое для нагревания одного моля вещества на 1К. Различают истинную и среднюю теплоемкости. Истинная - C = Q/dT Количество теплоты, переданное телу при постоянном объеме, равно приращению внутренней энергии тела . Количество теплоты, переданное телу припостоянном давлении, равно приращению энтальпии тела . Отсюда для истинной молярной теплоемкости при постоянном объеме и давлении получаем выражение:

Средняя-.

Все теплоемкости опред. Либо при постоянном давлении либо при постоянном объеме.

Все теплоемкости обладают свойствами складываемости. Теплоемкость тела будит складываться из его частей.

Зависимость теплоемкости от температуры записывается формулами: Сp=a + bt+ct^2+c”t^-2 –если присутствуют оба типа вещества Сp=a+bt+ct^2 – для орг.соединений и воды Сp=a+bt+c”t^-2 – для не орг.соединений.

2)В общем виде правило фаз Гиббса:

С=ЧислоТД параметров – число ур-й связ. параметры

Пусть наша система состоит из Ф фаз, каждая из которых содержит К компонентов. Независимыми ТД параметрами являются t и p. Дополнительными ТД параметрами явл. составы составы каждой из фаз. Для того что бы полностью описать составы системы нужно занать К-1 состав.

. Т.о. для полного описания состава всей гетерогенной системы, необходимо знать (к-1)ф состава , т.е. число ТД параметров будет равно:

Число ТДП =Ф(к-1)+pt/2

Для вывода числа ур-ий связывающие ТД параметры воспользуемся условиями фаз.равновесия т.к t и p фиксированы для всей системы, то основными уравнениями свзязывающими ТД , будут уравнения для хим. потенциалов. Если система содержит Ф фаз , то для описания потребуется ф-1, т.к. система содержит x компонентов, то общее число уравнений (ф-1). Правило фаз гиббса можно записать в виде:

С=ф(к-1)+2-к(ф-1)=фк-ф+2-кф+к

С=к-ф+2

С – число ТД степеней свободы

К-чило компонентов

Ф-число фаз

Св-ва конден.систем прак-ки не зависят от Р,поэтому числов внеш. факторов умен-ся на ед.,а по правилу фаз опр-ся так называемая условная вариантность системы:с=K-Ф+1.

Билет№5

1) Рассмотрим зависимость теплоты процесса при постоянном давлении от температуры. Возьмем частную производную по температуре от теплоты процесса Н при постоянном давлении или от теплоты процесса U при постоянном объеме:

Отсюда получаем

Где - изменение молярной теплоемкости в результате протекания процесса при p=const или V=const.

Уравнение (3) называют уравнениями Киргоффа; из них следует, что температурный коэффициент процесса равен изменению теплоемкости в результате протекания этого процесса.

Из уравнения (3) следует, что если изменение теплоемкости во время процесса положительно, то и тепловой эффект с ростом температуры становится более положительным :

При

и наоборот

при

При

Для вычисления теплового эффекта процесса при , если известен тепловой эффект процесса при , уравнение Киргофа (3) нужно проинтегрировать (10).

Аналогичное выражение получается для теплового эффекта процесса при постоянном объеме.

2)На границе раздела электроно- и ионопроводящих фаз, составляющих электрод, возникает разность потенциалов вследствие перехода заряженных частиц из одной фазы в другую. Эта разность потенциалов представляет собой так называемый электродный потенциал. Например, в случае электродов, состоящих из металла и раствора его соли (Cu2 + / Cu, Zn2 + / Zn), через межфазную границу переходят ионы металла и электроны, а электродная реакция

Me + ze- = Ме

является потенциалопределяющей. Если реакция равновесна, то есть протекает с одинаковой скоростью в прямом и обратном направлениях, то на электроде реализуется равновесный потенциал. Водороднай шкала:

Наиболее часто в качестве электрода сравнения (эталона) принято использовать водородный электрод. Поэтому измеряют напряжение гальванического элемента, составленного из исследуемого и стандартного водородного электрода, стандартный электродный потенциал которого принимают равным нулю. Схему такого элемента записывают следующим образом: слева - водородный электрод, справа - измеряемый электрод. Например, схема гальванического элемента для измерения потенциала цинкового электрода имеет вид: H₂, Pt | H⁺|| Zn²⁺| Zn, а схема элемента для измерения потенциала медного электрода: H₂, Pt | H⁺|| Cu²⁺| Cu, Напряжение гальванического элемента равна разности потенциалов правого и левого электродов: А так как потенциал левого электрода условно принимают равным нулю, то напряжение измеряемого элемента будет равна потенциалу правого электрода, т.е. стандартному электродному потенциалу. Для водородно-цинкового элемента напряжение равно: т.е. водородный электрод заряжен менее отрицательно, чем цинковый. Таким образом, во внешней цепи электроны перемещаются от цинкового электрода к водородному. Для медно-водородного электрода: т.е. медный электрод заряжен более положительно, чем водородный. Таким образом, во внешней цепи электроны перемещаются от водородного электрода к медному. Тогда стандартное напряжение для элемента Даниэля-Якоби равно:

Билет№7

1)Фомулировки: 1)Тепло может переходить от более нагретого тела к менее нагретому. 2)Тело имеющую наименьшую температуру, не может быть источником тепла. 3)Невозможно создать вечный двигатель 2-ого рода, то есть такую машину, которая переводила бы все подведенное к ней тепло в работу.

Второе начало термодинамики носит статистический характер и применимо только к системам из большого числа частиц. Второе начало термодинамики, так же как и первое начало, является постулатом. . . Процессы, которые совершаются в системе без вмешательства со стороны окружающей среды, называются самопроизвольными. Процессы, которые без «вмешательства извне» сами собой совершаться не могут, называются несамопроизвольными. Необратимыми процессами называются такие процессы, после протекания которых систему и окружающую среду одновременно нельзя вернуть в прежнее состояние. Обратимыми процессами называются такие процессы, после которых можно вернуть и систему, и окражующую среду в прежнее состояние.

Общая математическая формула 2ого закона:

и . S- ‘энтропия, служит мерой той части энергии, которая не может быть превращена в работу, при переодическом действии машин.

Основной задачей термодинамики является предсказание возможности протекания процесса. Поэтому введено понятие критерия направленности, такой велечины посмотрев на которую можно точно сказать будет ли процес самопроизвольным. Для этого объединим матем.фомулировки 1ого и 2ого законов.

SQ=dU+ ; dS cледует TdS =dU+

TdS dU+ или TdS dU+pdV+

Для изолированной системы:

U=const cледует dU=0

V=const cледует pdV=0

= 0; dS . В изолир.системе могут протекать только самопроизвольные процессы, поэтому все сам.произвол. процессы должны протекать с ростом энтропии. Если самопроизв.процес подошел к концу, тоесть наступило равновесие, рост энтропии прекращяется и ее изменение становится равным 0.

2)E1-2=E1-2=E2-2 – идеальные растворы

= +RTlnPi

= +RTlnXi

+RTlnXi

=

=

Pi= *Xi – Закон Рауля.

Растворы, компоненты которых различаются по физическим и химическим свойствам, подчиняются закону Рауля лишь в области очень малых концентраций; при больших концентрациях наблюдаются отклонения от закона Рауля. Случай, когда истинные парциальные давления паров над смесью больше, чем вычисленные по закону Рауля, называютположительными отклонениями. Противоположный случай, когда парциальные давления паров компонентов оказываются меньше вычисленных — отрицательные отклонения.

Причиной отклонений от закона Рауля является то обстоятельство, что однородные частицы взаимодействуют друг с другом иначе, чем разнородные (сильнее в случае положительных и слабее в случае отрицательных отклонений).

Реальные растворы с положительными отклонениями от закона Рауля образуются из чистых компонентов с поглощением теплоты (ΔН_раств > 0); объём раствора оказывается больше, чем сумма исходных объёмов компонентов (ΔV > 0). Растворы с отрицательными отклонениями от закона Рауля образуются с выделением теплоты (ΔН_раств < 0); объём раствора в этом случае будет меньше, чем сумма исходных объёмов компонентов (ΔV < 0).

Билет№9

1)Величина S называется энтропией и служит мерой той части энергии , которая не может быть превращена в работу. В тоже время энтропия является функцией состояния , поэтому Sобр.= необр.= .

С другой стороны энтропия служит мерой упорядоченности системы, это определение вытекает из трактования энтальпии которое предложил Больцман: S=klnW.

При протекании любова процесса энтропия меняется, т.к. меняются состояния характеризующие систему, следовательно и параметры характериз. систему. Наиболее часто рассматривают два вида процесса:

1)фазовый переход. Тв---ж; Тв—газ; жид --- газ.

Так как изменение энтропии в любом процессе одинаково для обратимого и не обратимого протекания, в теорет.записи можно использовать знак равно.

dS= . Теплота необходимая для фазового перехода наз.теплотой фазового перехода. tr

tr = . Следовательно любые фазовые переходы являются самопроизвольными в отличие от обратных.

2)Нагревание. Чаще всего нагревание рассматривают для конденсированных и газообразн. систем , работа расширения принимается равной 0, т.к. W=p .

V=const. В этом случае ln . Аналагично для изохорного нагревания. Сложнее с газообразными системами, т.к.учитывается работа расширения, в этом случае объем меняется столь значительно, что принебречь его изменением не возможно.

Уравнения для расчета энтропии для различных систем:

Изотермический процесс (Т=const): ΔS= (V=const) ΔS= (P=const)

Изобарный процесс (P=const): ΔS= ; ΔC_p=const; ΔS=nC_pln

Изохорный процесс (V=const): ΔS= ; ΔC_v=const; ΔS=nC_vln