Контрольная работа по математике (для студентов озо: I курс, Профессиональное обучение (ивт)) Демонстрационный вариант
Задача
1.
Найдите
.
Решение:
Находим тригонометрическую форму
комплексного числа z
= 1 + i:
x
= Re(z)
= 1, y
= Im(z)
= 1 > 0, |z|
=
,
=
.
Таким
образом, 1 +
i
=
– тригонометрическая форма комплексного
числа z
= 1 + i
.
Извлекаем
корень:
(k
= 0, 1, 2).
Итак,
Ответ:
z0
=
,
z1
=
,
z2
=
.
Задача 2. Решите методом Гаусса систему линейных уравнений
Решение: 1) Составляем расширенную матрицу системы:
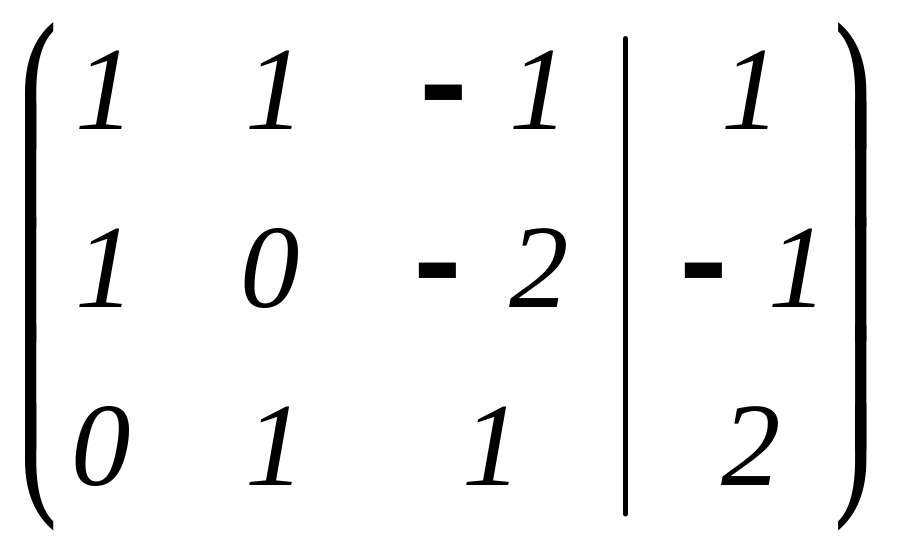
2) Приводим эту матрицу к каноническому ступенчатому виду:
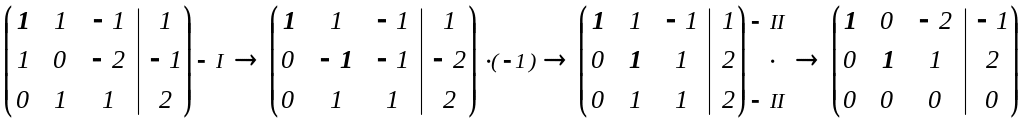
3) Составляем равносильную каноническую систему:
,
4) Находим общее решение:
5) Система совместна (решения есть), но не определена (решение не единственно)
Ответ:
Задача 2. Решите методом Гаусса систему линейных уравнений
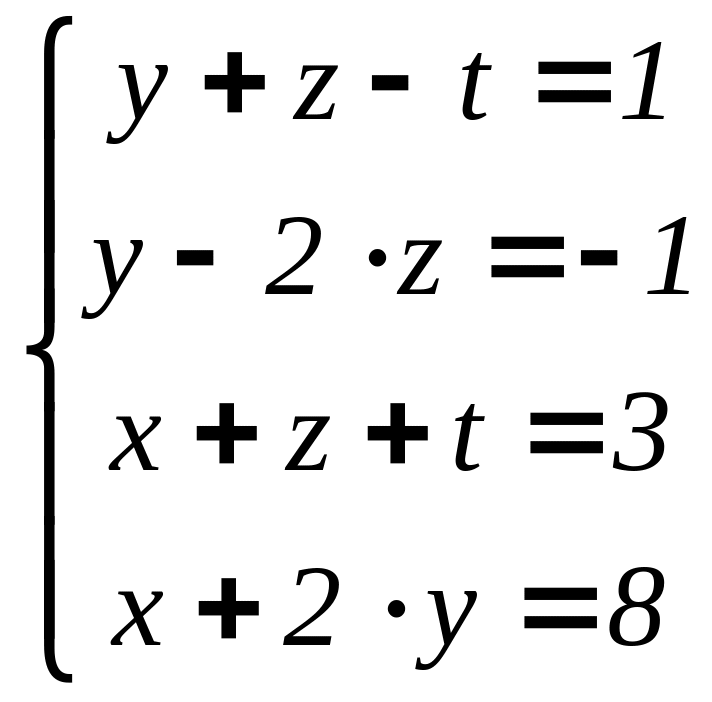
Решение: 1) Составляем расширенную матрицу системы:
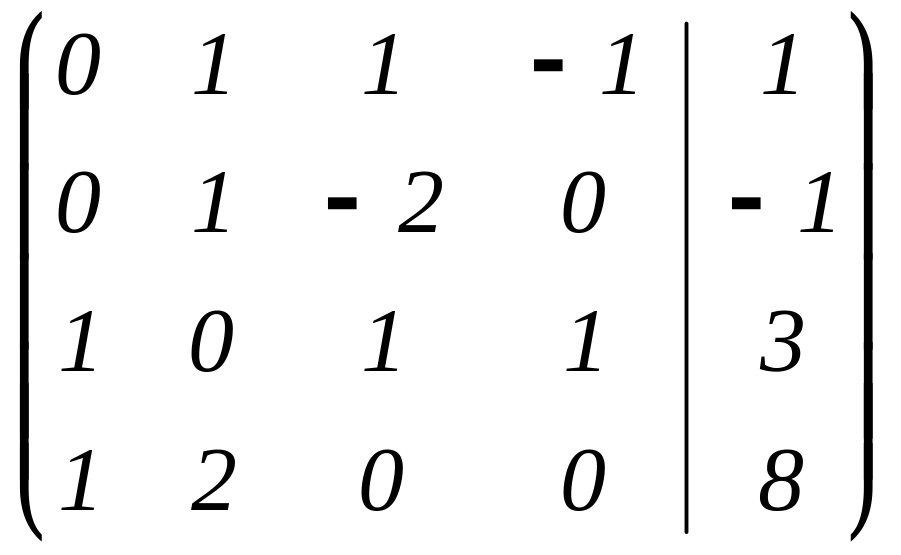
2) Приводим эту матрицу к каноническому ступенчатому виду:
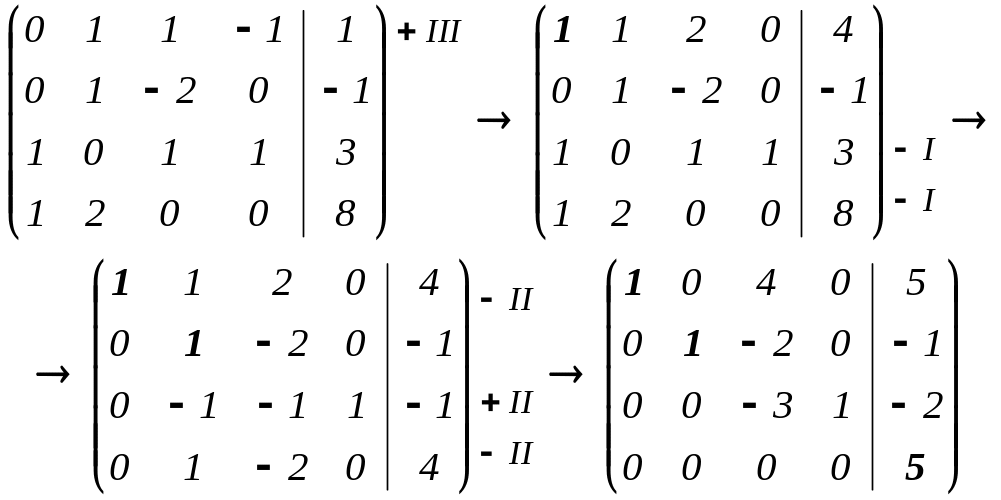
5) Система несовместна (не имеет решений), т.к. главный элемент находится в правой её части.
Ответ: система несовместна.
Задача 3. Двумя способами решите матричное уравнение:
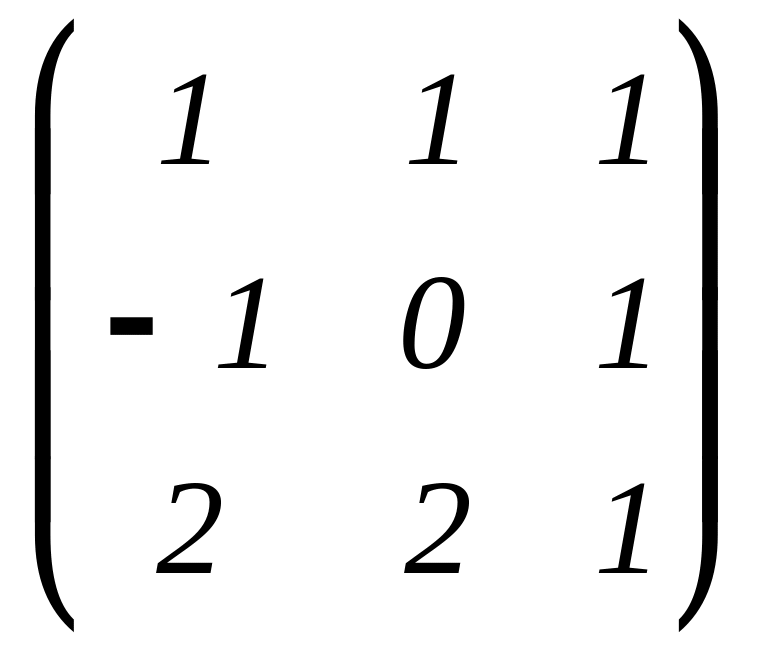X
=
.
Решение: I. Элементарные преобразования строк.
1) Составляем расширенную матрицу
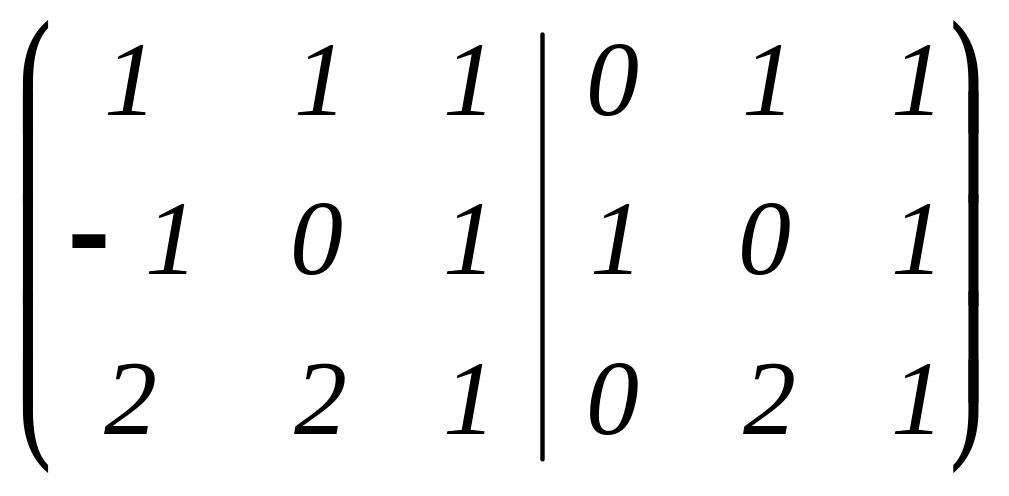
2) Приводим эту матрицу к каноническому виду:
Ответ:
X
=
.
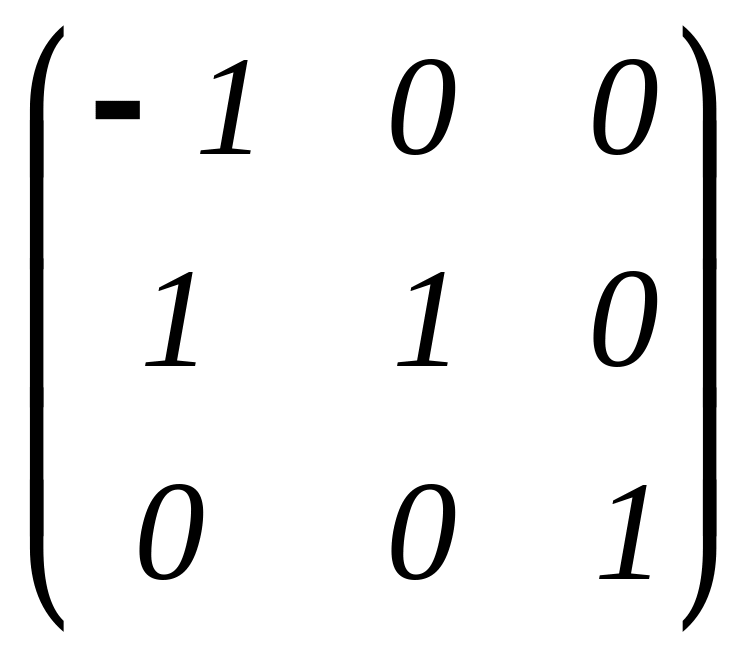3)
Проверка:
.
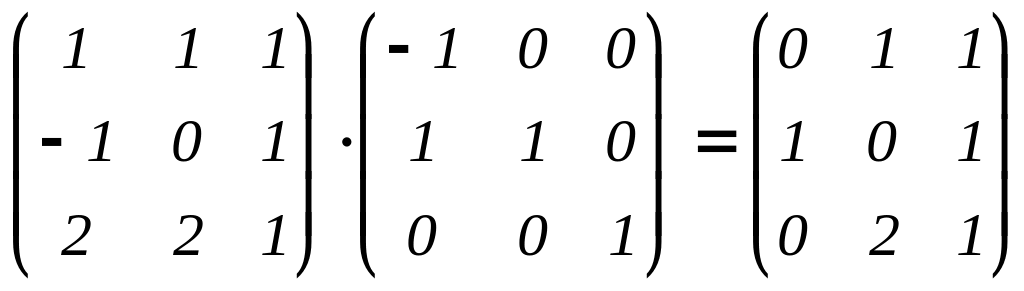II. С помощью обратной матрицы.
1)
Находим определитель матрицы A
=
:
=
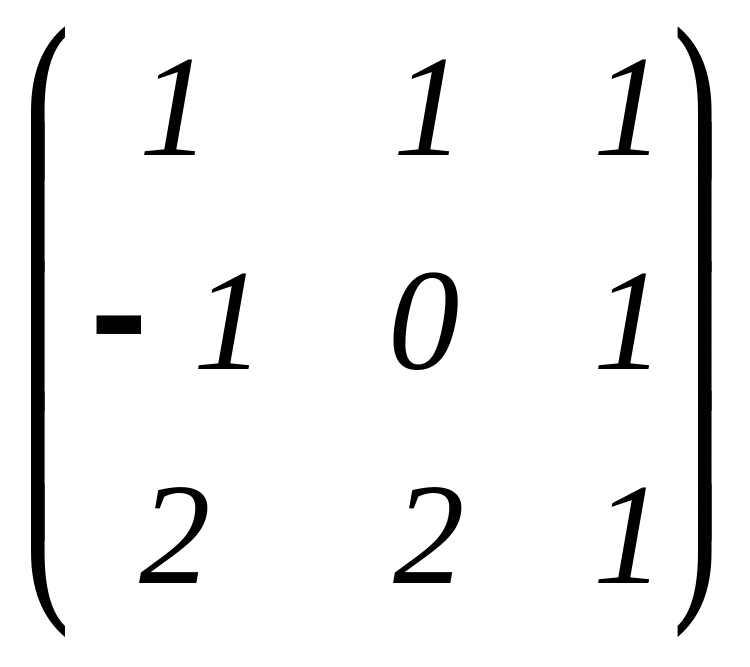(101
+ 112
+ (–1)21)
– (102
+ (–1)11
+ 112)
= –1
0
Значит, обратная матрица существует.
2) Находим все алгебраические дополнения к элементам исходной матрицы:
А11
= +
= –2, А12
= –
= 3, А13
= +
= –2,
А21
= –
= 1, А22
= +
= –1, А23
= –
= 0,
А31
= +
= 1, А32
= –
= –2, А33
= +
= 1.
3)
Составляем обратную матрицу: А
–1 =
(Аij)
t
4) Находим решение уравнения X = A–1B:
X
=
Ответ: X = .
Задача 4. Для параллелепипеда ABCDA1B1C1D1 с вершинами A(–1; 1; 0), B(0; –1; 0), C(1; 0; –1), B1(–2; –1; –2) найдите: а) его объём V, б) площадь SABCD грани ABCD, в) каноническое уравнение прямой l = (B1A1), г) угол ((ABB1), (ABD)) между гранями (ABB1) и (ABD).
Решение:
а)
Поскольку
(–1;
2; 0),
(–2;
0; –2),
(1;
1; –1), то
V
= |
|
=
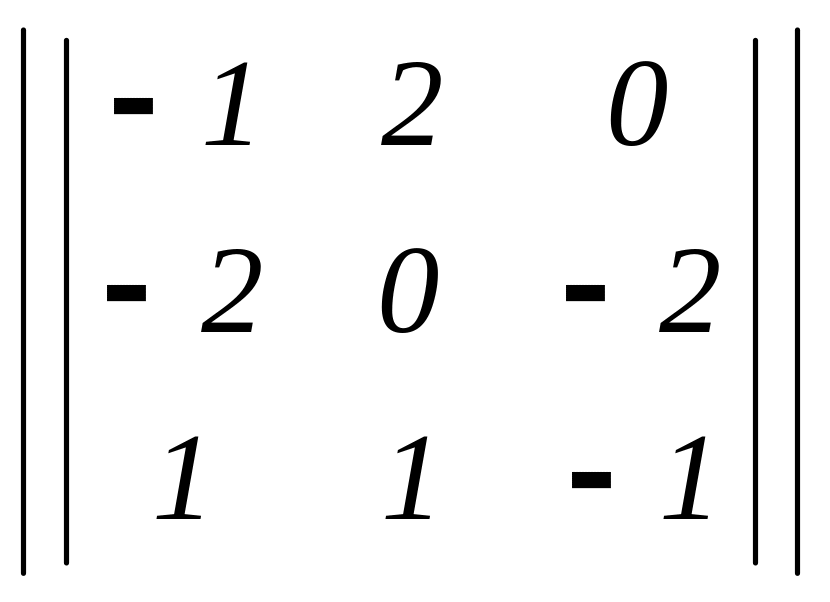= |(0 – 4 + 0) – (0 –2 – 4)| = 2.
б)
Поскольку
(–1;
2; 0),
(1;
1; –1), то
SABCD
= |
|
=
=
= |i
– j
+ k
|
= |–2i
– j
– 3k|
=
=
=
.
в)
Найдём координаты точки A1
, используя свойство параллелепипеда
,
т.е. x
– (–1) = –2, y
– 1 = 0, z
– 0 = –2 или
A1(–3;
1; –2).
Направляющий
вектор прямой (AA1)
равен
(–2;
0; –2). Поэтому
каноническое
уравнение (AA1):
.
г) Запишем общие уравнения плоскостей (ABD) = (ABC) и (ABB1). Их направляющие векторы: (–1; 2; 0), (1; 1; –1) и (–1; 2; 0), (–2; 0; –2) соответственно. Поэтому
(ABD):
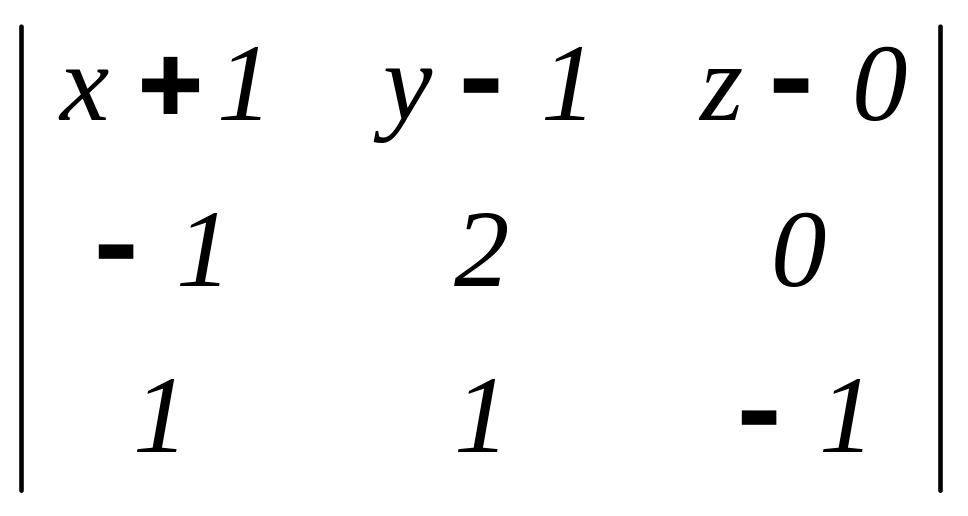= 0
(x + 1)(–2)
– (y – 1)1
+ z(–3)=
0
2x + y + 3z + 1 = 0.
(ABB1):
= 0
(x + 1)(–4)
– (y – 1)2
+ z4
= 0
4x + 2y – 4z + 2 = 0.
Таким образом, перпендикулярные к этим плоскостям векторы таковы: N(2; 1; 3) (ABD), M(4; 2; –4) (ABB1). Поэтому
((ABB1),
(ABD)) = arc cos
= arc cos
=
=
arc cos
= arc cos
.
Ответ:
а)
V
= 2,
б)
SABCD
=
, в)
канон
(AA1):
, г)
((ABB1),
(ABD)) = arc cos
.
Задача
5.
Найдите
производную y(x):
а)
, б)
y
= ln(tg
),
в)
y
= arc
cos(e
x
– 3),
г)
x3
+ e2y
– y2
= 1.
Решение: Используем правила дифференцирования и таблицу производных.
а) .
y
= ((x4
– 1)1
/ 5)
+ ((x5
+ 1)1
/ 4)
=
=
.
б) y = ln(tg ).
в) y = arc cos(e x – 3).
г) x3 + e2y – y2 = 1.
Это
неявная функция
F(x,
y)
= 0, где F(x,
y)
= x3
+ e2y
– y2
– 1. Поэтому
y(x)
=
.
Имеем
Fx
=
= 3x2,
Fy
=
= 2e2y
– 2y,
и y(x)
=
.
Задача
6.
Исследуйте
функцию и постройте график: y
=
.
Решение: Действуем согласно схеме исследования функции y = f(x).