Содержание
Лабораторная работа № 1 2
Программный вывод: 4
Лабораторная работа № 2 5
Программный вывод: 7
7
Лабораторная работа № 3 9
Программный вывод: 11
Лабораторная работа № 4 13
Программный вывод: 15
Лабораторная работа № 5 17
Программный вывод: 19
Лабораторная работа № 6 20
Код программы: метод Зейделя 24
Лабораторная работа № 7 25
Оценка погрешности приближения F(eps). 26
Контрольная работа № 2 28
Лабораторная работа № 1
Тема: Решение нелинейных уравнений. Метод половинного деления.
Задание:
1. Отделить корни уравнения
графически и программно.
Уточнить корни уравнения методом половинного деления с точностью
.
Решение задачи.
Отделим корни уравнения на отрезке
графическим методом. Для этого табулируем
функцию
на данном отрезке.
Имеем
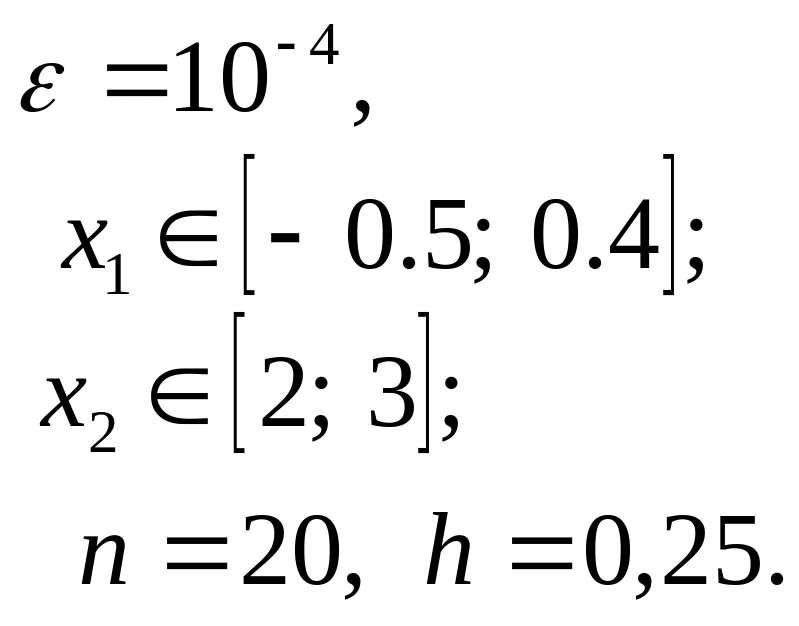
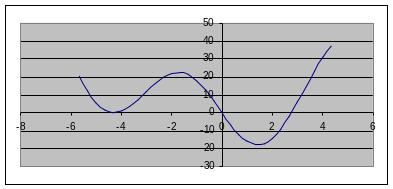
Выделим отрезок
,
содержащий изолированный корень, для
уточнения которого применим метод
половинного деления по схеме
,
,
,
где
,
.
При условии остановки деления отрезка
пополам
,
составим таблицу
a |
b |
(a+b)/2 |
f(a) |
f(b) |
f((a+b)/2) |
корень |
погрешн |
усл ост |
-0,5 |
0,4 |
-0,05 |
9,838510772 |
-7,628366846 |
1,002083 |
|
0,05 |
нет |
-0,05 |
0,4 |
0,175 |
1,002083385 |
-7,628366846 |
-3,45154 |
|
0,175 |
нет |
-0,05 |
0,175 |
0,0625 |
1,002083385 |
-3,451537752 |
-1,24528 |
|
0,0625 |
нет |
-0,05 |
0,0625 |
0,00625 |
1,002083385 |
-1,245280107 |
-0,12496 |
|
0,00625 |
нет |
-0,05 |
0,00625 |
-0,021875 |
1,002083385 |
-0,124960124 |
0,437944 |
|
0,021875 |
нет |
-0,021875 |
0,00625 |
-0,0078125 |
0,437943625 |
-0,124960124 |
0,156309 |
|
0,007812 |
нет |
-0,0078125 |
0,00625 |
-0,00078125 |
0,156309446 |
-0,124960124 |
0,015626 |
|
0,000781 |
нет |
-0,00078125 |
0,00625 |
0,00273438 |
0,015625609 |
-0,124960124 |
-0,05468 |
|
0,002734 |
нет |
-0,00078125 |
0,002734375 |
0,00097656 |
0,015625609 |
-0,054679955 |
-0,01953 |
|
0,000977 |
нет |
-0,00078125 |
0,000976563 |
9,7656E-05 |
0,015625609 |
-0,019530293 |
-0,00195 |
9,766E-05 |
9,77E-05 |
да |
-0,00078125 |
9,76563E-05 |
-0,0003418 |
0,015625609 |
-0,001953115 |
0,006836 |
|
0,000342 |
нет |
-0,0003418 |
9,76563E-05 |
-0,00012207 |
0,006836054 |
-0,001953115 |
0,002441 |
|
0,000122 |
нет |
-0,00012207 |
9,76563E-05 |
-1,2207E-05 |
0,002441421 |
-0,001953115 |
0,000244 |
-1,221E-05 |
1,22E-05 |
да |
-1,2207E-05 |
9,76563E-05 |
4,2725E-05 |
0,000244141 |
-0,001953115 |
-0,00085 |
4,272E-05 |
4,27E-05 |
да |
-1,2207E-05 |
4,27246E-05 |
1,5259E-05 |
0,000244141 |
-0,00085449 |
-0,00031 |
1,526E-05 |
1,53E-05 |
да |
-1,2207E-05 |
1,52588E-05 |
1,5259E-06 |
0,000244141 |
-0,000305176 |
-3,1E-05 |
1,526E-06 |
1,53E-06 |
да |
Приближенное
решение
,
погрешность
,
число итераций
.
Следовательно, приближенное значение
корня равно
.
Запишем приближенное значение корня
только верными значащими цифрами в
узком смысле: имеем
,
,
.
Округлим
до
.
Получим
,
,
.
Найдем число верных
знаков для
.
Имеем
,
,
.
Так как
,
то получим приближенное значение корня
с числом верных знаков
.
Ответ:
.
Выделим отрезок
,
содержащий изолированный корень, для
уточнения которого применим метод
половинного деления по схеме
,
,
,
где
,
.
При условии остановки деления отрезка
пополам
,
составим таблицу
a |
b |
(a+b)/2 |
f(a) |
f(b) |
f((a+b)/2) |
корень |
погрешность |
усл ост |
2 |
3 |
2,5 |
-14,18595 |
6,1776 |
-5,7194429 |
|
5,7194 |
нет |
2,5 |
3 |
2,75 |
-5,719443 |
6,1776 |
-0,0707198 |
|
0,0707 |
нет |
2,75 |
3 |
2,875 |
-0,07072 |
6,1776 |
2,99670513 |
|
2,9967 |
нет |
2,75 |
2,875 |
2,813 |
-0,07072 |
2,996705 |
1,44646611 |
|
1,4465 |
нет |
2,75 |
2,8125 |
2,781 |
-0,07072 |
1,446466 |
0,68345354 |
|
0,6835 |
нет |
2,75 |
2,78125 |
2,766 |
-0,07072 |
0,683454 |
0,30522631 |
|
0,3052 |
нет |
2,75 |
2,765625 |
2,758 |
-0,07072 |
0,305226 |
0,11696367 |
|
0,117 |
нет |
2,75 |
2,757813 |
2,754 |
-0,07072 |
0,116964 |
0,02304897 |
|
0,023 |
нет |
2,75 |
2,753906 |
2,752 |
-0,07072 |
0,023049 |
-0,0238537 |
|
0,0239 |
нет |
2,751953 |
2,753906 |
2,753 |
-0,023854 |
0,023049 |
-0,000407 |
|
0,0004 |
нет |
2,75293 |
2,753906 |
2,753 |
-0,000407 |
0,023049 |
0,01131987 |
|
0,0113 |
нет |
2,75293 |
2,753418 |
2,753 |
-0,000407 |
0,01132 |
0,00545617 |
|
0,0055 |
нет |
2,75293 |
2,753174 |
2,753 |
-0,000407 |
0,005456 |
0,00252454 |
|
0,0025 |
нет |
2,75293 |
2,753052 |
2,753 |
-0,000407 |
0,002525 |
0,00105877 |
|
0,0011 |
нет |
2,75293 |
2,752991 |
2,753 |
-0,000407 |
0,001059 |
0,00032591 |
|
0,0003 |
нет |
2,75293 |
2,75296 |
2,753 |
-0,000407 |
0,000326 |
-4,052E-05 |
2,752944946 |
4E-05 |
да |
2,752945 |
2,75296 |
2,753 |
-4,05E-05 |
0,000326 |
0,00014269 |
|
0,0001 |
нет |
2,752945 |
2,752953 |
2,753 |
-4,05E-05 |
0,000143 |
5,1083E-05 |
2,752948761 |
5E-05 |
да |
2,752945 |
2,752949 |
2,753 |
-4,05E-05 |
5,11E-05 |
5,2788E-06 |
2,752946854 |
5E-06 |
да |
Приближенное
решение
,
погрешность
,
число итераций
.
Следовательно, приближенное значение
корня равно
.
Запишем приближенное значение корня
только верными значащими цифрами в
узком смысле: имеем
,
,
.
Округлим
до
.
Получим
,
,
.
Найдем число верных
знаков для
.
Имеем
,
,
.
Так как
,
то получим приближенное значение корня
с числом верных знаков
.
Ответ:
.