Центр тяжести

На отдельные частицы, из которых состоит твердое тело, действуют силы тяжести практически параллельно (при расстоянии между частицами в 31 м угол между вертикалями сил их тяжести составляет одну угловую секунду).

Равнодействующая сил тяжести всех частиц тела называется силой тяжести этого тела.

Как бы не изменялось положение тела в пространстве, силы тяжести его отдельных частиц останутся вертикальными и практически параллельными одна другой. Из основного свойства равнодействующей системы параллельных сил известно, что она всегда проходит через одну и ту же точку – центр данной системы параллельных сил. Отсюда понятие центра тяжести:

Центр тяжести – неизменно связанная с телом точка, через которую проходит линия действия силы тяжести данного тела при любом положении тела в пространстве.

Координаты центра тяжести любого твердого тела можно определить по формулам:

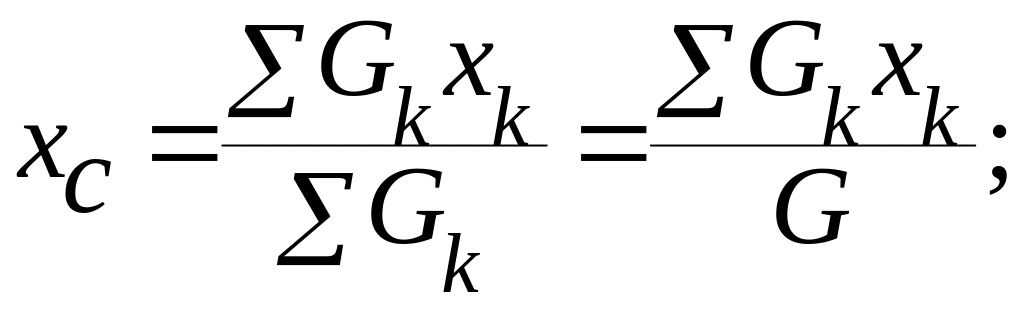
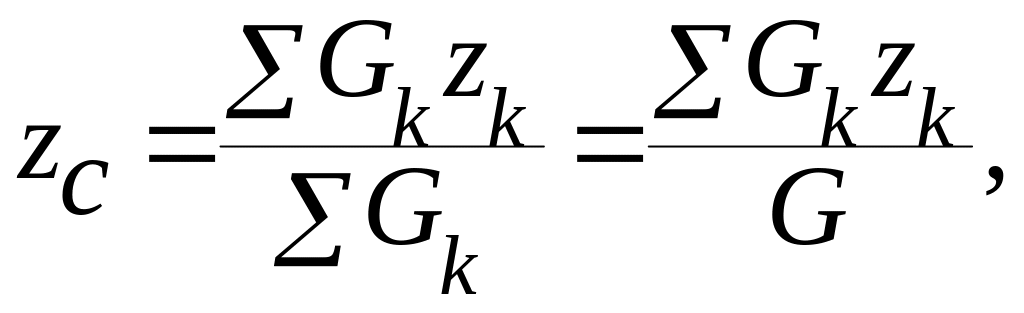
где G_k – сила тяжести произвольной частицы тела;

x_k, y_k, z_k – координаты этой частицы;

G – сила тяжести всего тела

Для плоских фигур координата центра тяжести z_k из уравнений исключается. Координаты центра тяжести для любой плоской фигуры просто определяются с помощью понятия «статический момент». Статический момент площади всей фигуры:

Статический момент имеет размерность: мм³, см³, м³.

Из этих уравнений легко определить координаты центра тяжести плоской фигуры:

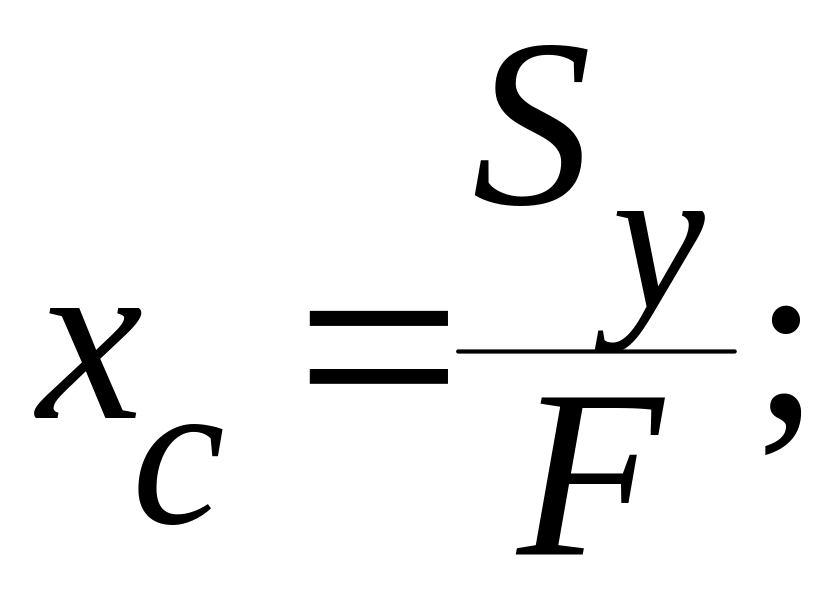
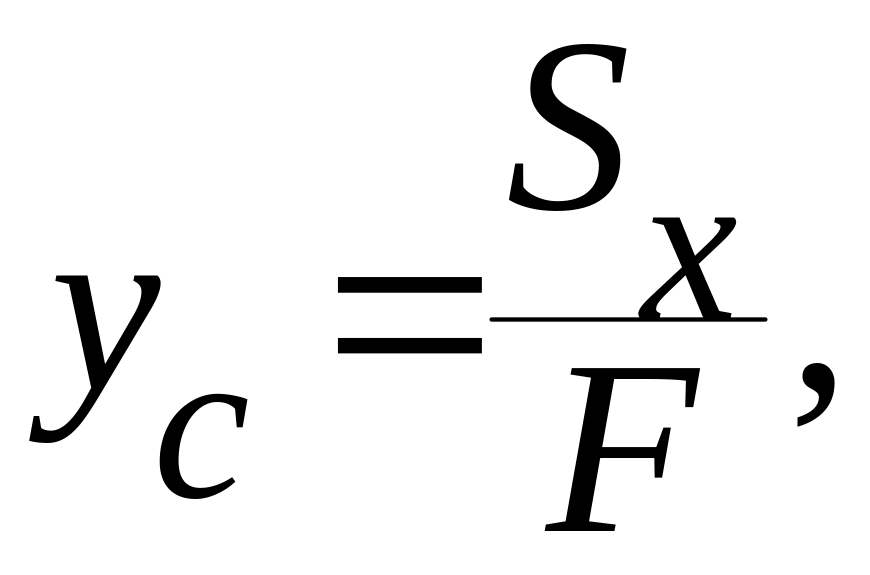
где F – площадь всей фигуры.

Пример 6. Определение центра тяжести плоского сечения

Определить статические моменты относительно координатных осей и положение центра тяжести сечения, составленного из равнобокого уголка № 10, швеллера № 24 и полосы 190 10

(рисунок 20).

И з таблиц сортамента прокатной стали [1] выпишем данные:

1) для равнобокого уголка № 10 ширина полки В = 100 мм, толщина полки S = 10 мм, площадь поперечного сечения F = 19,2 см², расстояние центра тяжести от наружных краев стенок x₀ = y₀ = 2,83 см;

2) для швеллера № 24 высота стенки Н = 240 мм, ширина полки В = 90 мм, толщина стенок S = 5,6 мм, площадь сечения F = 30,6 см², расстояние центра тяжести от наружного края вертикальной стенки х₀ = 2,42 см, горизонтальная ось швеллера является осью симметрии,

следовательно, его центр тяжести лежит на этой оси;

3 ) полоса имеет прямоугольное сечение, ее площадь F = 19 см², центр тяжести лежит на пересечении осей симметрии.

Рисунок 20 – Сложное сечение (размеры указаны в см)

Пронумеруем отдельные части сечения: уголок 1, швеллер 2, полоса 3. Выберем оси координат, определим относительно этих осей координаты центров тяжести частей фигуры и вычислим их статические моменты. Определим суммарную площадь всего сечения и суммарные статические моменты сечения. Результаты удобно свести в таблицу 11.

Таблица 11 – Определение статических моментов

Часть сечения	Площадь Fk, см2	Координата центров тяжести, см		Статический момент, см3
		xk	yk	Syk	Sxk
1	19,2	7,17	3,83	137,66	73,54
2	30,6	12,42	13,00	380,05	397,80
3	19,0	9,50	0,50	18,50	9,50
Суммарная величина	= 68,8	–	–	Sy = = 698,21	Sx = = 480,84

Вычислим суммарную площадь сечения плоской фигуры:

см².

Определим статические моменты сечения относительно координатных осей

Относительно оси y:

см³;

см³;

см³.

Относительно оси х:

см³;

см³;

см³.

Суммарные статические моменты:

см³;

см³.

Результаты внесем в таблицу 11.

Координаты центра тяжести сечения:

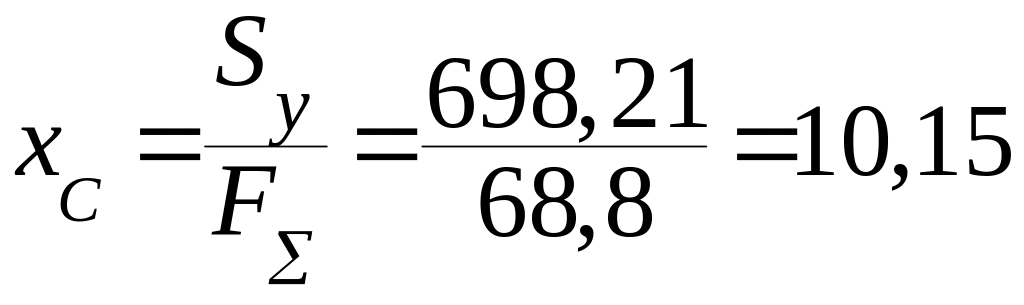см;

см.

Нанесем центр тяжести С сечения на чертеж.

Задание 6

Определить положение центра тяжести плоской фигуры, составленной из пластин и стандартных профилей, применяющихся в авиастроении.

1 Координаты центра тяжести следует определять через статические моменты плоских фигур. Результаты расчетов удобно свести в таблицу, как показано в примере 6.

2 Центры тяжести простых геометрических фигур лежат в их геометрических центрах; для фигур, имеющих оси симметрии, центр тяжести лежит на этих осях. Для несимметричных прокатных профилей координаты x₀ и y₀ центра тяжести указаны в таблицах 12 и 13.

3 Для каждой схемы в соответствии с вариантом задания следует вычертить три заданных профиля в масштабе М 1:1 (можно на миллиметровой бумаге) без зазоров, так как указанные профили соединяются сваркой. Схемы заданий приведены в таблице 14, варианты схем заданий – в таблице 15.

4 Провести оси координат, определить площади фигур (или выписать их из таблицы 13). Определить координаты центров тяжести плоских сечений относительно осей координат. Все результаты внести в таблицу, аналогичную таблице 11.

5 Вычислить статические моменты плоских сечений и результаты вычислений внести в таблицу, аналогичную таблице 11.

6 Определить координаты центра тяжести всей плоской фигуры по формулам:

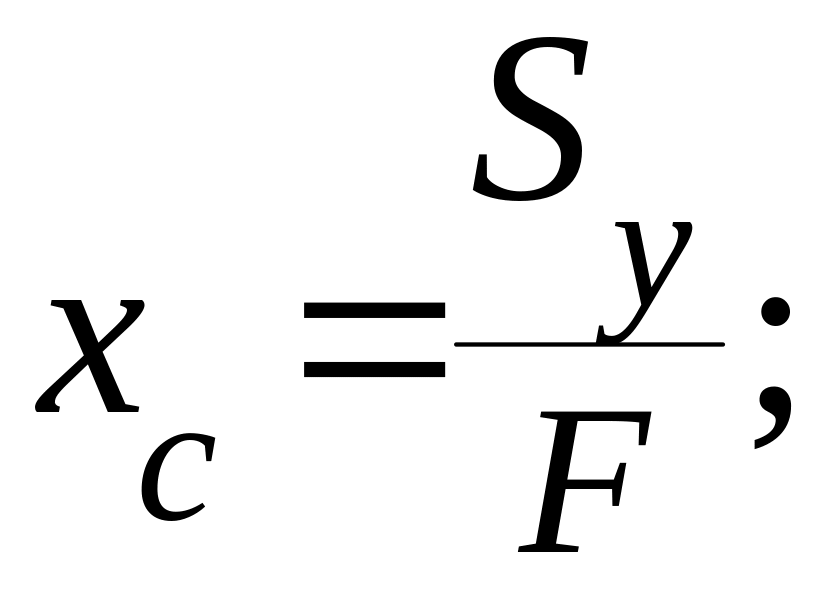
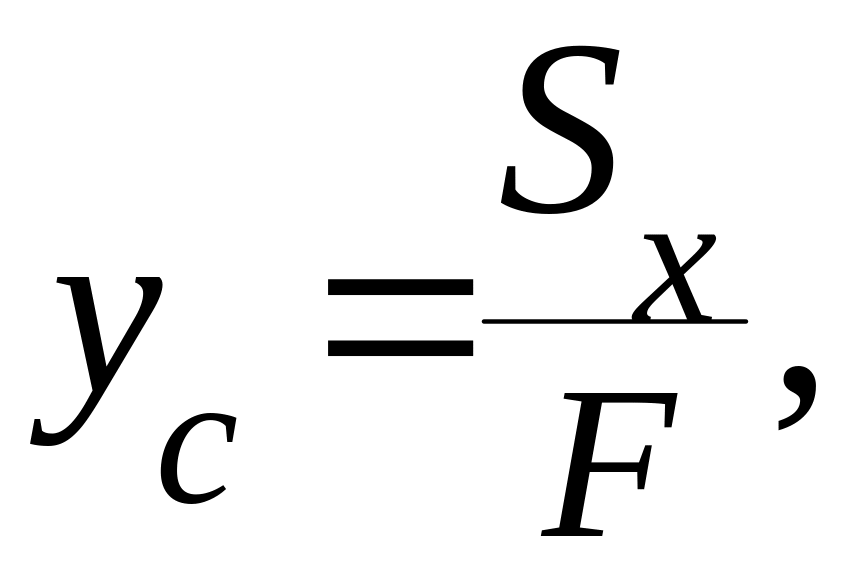
нанести центр тяжести на чертеж плоской фигуры. При вычислениях следует обратить внимание на единицы измерений, так как в таблице 13 площади сечений стандартных профилей приведены в см².

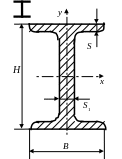
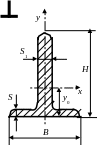
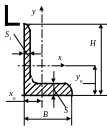
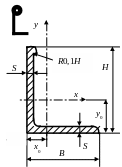
Таблица 12 – Координаты центров тяжести авиационных профилей

Таблица 13 – Геометрические параметры стандартных авиационных профилей

Наименование профиля	Номер профи-ля	Площадь сечения, см2	Размер, мм
			H	B	S	S1	x0	y0
Двутавр	6	5,15	50	50	2.5	4	-	-
Тавр разностенный	4	2,35	35	40	2.5	4	-	10,8
Угольник разностенный неравнобокий	26	4,43	65	40	5	4	10,0	20,0
Бульбоугольник	5	1,16	30	20	2	-	4,57	12,5
Зет-нормальный	12	5,18	50	35	5	4	-	-

Таблица 14 – Схемы к заданию 6

С Д Ж 70х4 В А Б Е 25х4 Г 45х4 45х4 хемы 1…10

Д Ж 50х4 Г 50х6 А Б 50х4 В Е 74х4 Схемы 11…20

Д Ж 30х4 С Е 30х4 № 5 А В Б 40х4 Г 60х4 хемы 21…30

К схемам в таблице 14, в которой размеры листов указаны в мм, по таблице 15 выбираем варианты заданий в соответствии с буквенными шифрами. В каждом из заданий имеются только три профиля. Например, для шифра АБД схемы 1 выбраны профили А – зет-нормальный, лист Б – 45 × 4 мм и угольник Д разностенный неравнобокий. Для схемы 2 варианта 2 выбран шифр АБГ – профили А – зет- нормальный, лист Б – 45 × 4 мм и лист Г – 45 × 4 мм.

Таблица 15 – Варианты к заданию 6

Номер схемы	Шифр по вариантам
	1	2	3	4	5	6	7	8	9	10
1…10	АБД	АБГ	АБВ	АГД	АВГ	АБЕ	БВЕ	АВЕ	АВЖ	БВЖ

Продолжение таблицы 15

Номер схемы	Шифр по вариантам
	11	12	13	14	15	16	17	18	19	20
11…20	АБВ	АБГ	АГД	АБЕ	БВЕ	АГЕ	АВЕ	АГЖ	ГДЖ	АБЖ

Окончание таблицы 15

Номер схемы	Шифр по вариантам
	21	22	23	24	25	26	27	28	29	30
21…30	АБВ	АБД	АГД	АГЕ	ГДЕ	АБЖ	БВЖ	АДЖ	АБГ	АГЖ