Плоская система произвольных сил

В большинстве задач теоретической механики имеют дело с несвободными телами, которые тем или иным способом соединены с другими телами, ограничивающими свободу перемещения несвободных тел. Тела, ограничивающие свободу перемещения рассматриваемого тела, называются связями. Если данное тело под действием приложенных к нему силовых факторов будет давить на связь, то и связь будет действовать на тело, препятствуя его движению с силой, которая называется реакцией связи (или реакцией). По четвертой аксиоме статики реакция равна по модулю давлению на связь и направлена в сторону, противоположную этой силе. К несвободному телу применяют уравнения равновесия, если в число действующих сил включить и силы реакций связей (по шестой аксиоме статики). Схемы подобного рода используются при расчетах конструкций воздушных судов и их двигателей.

Существующее многообразие опор механических конструкций сводится к трем основным типам (рисунок 9).

Рисунок 9 – Основные типы опор:

а – шарнирно-подвижная; б – шарнирно-неподвижная; в – защемление

В шарнирно-подвижной опоре, где связь не препятствует горизонтальному перемещению, возникает только нормальная реакция R_A (рисунок 9, а). В шарнирно-неподвижной опоре, препятствующей и горизонтальному, и вертикальному перемещениям, реакция связи неизвестна ни по модулю, ни по направлению. В этом случае применяют разложение неизвестной реакции на горизонтальную X_A и вертикальную Y_A составляющие (рисунок 9, б). Составляющие реакции неизвестны только по модулю. После их определения по уравнениям равновесия можно найти полную реакцию R_A по третьей аксиоме статики и ее направление по уравнениям направляющих косинусов. При разложении реакции на составляющие можно не обращать внимания на правильность выбора их направлений. Если в действительности составляющая будет направлена в противоположную сторону, то при вычислениях для нее будет получено отрицательное значение. В защемлении, препятствующем любому перемещению и вращению, кроме неизвестной в общем случае по модулю и направлению реакции, возникает реактивный момент m_R (рисунок 9, в), направление вращательного действия которого определяется полученным при вычислениях положительным или отрицательным значением.

Вертикальная сосредоточенная сила F вызывает в опорах только вертикальные реакции; наклонная сила F₁ в шарнирно-неподвижной опоре и в защемлении вызовет наклонные реакции (рисунок 10, а). Для их определения следует применять разложение сил и реакций на составляющие по горизонтальной и вертикальной осям.

Распределенная нагрузка интенсивностью p сводится к

равнодействующей сосредоточенной силе (для случая равномерно распределенной нагрузки); линия действия равнодействующей P будет проходить через центр тяжести той фигуры, которую образует на чертеже распределенная нагрузка (рисунок 10, б) – в указанном случае это прямоугольник.

Действие вращающего момента М полностью определяется его модулем и направлением (знаком момента) и учитывается только в уравнениях моментов (рисунок 10, в).

Р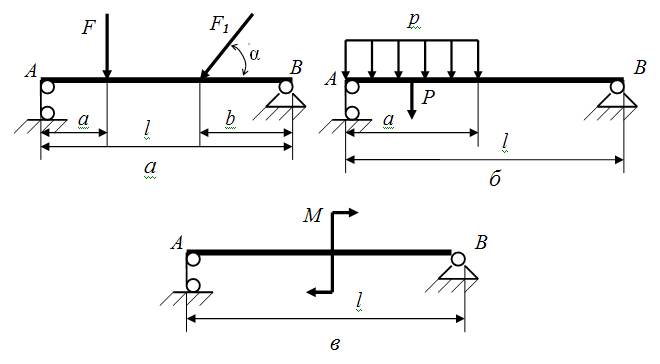 исунок 10 – Силовые факторы в конструкциях:

а – сосредоточенные силы; б – равномерно распределенная нагрузка;

в – вращающий момент

Пример 4. Определение реакций опор

Двухконсольная балка AD нагружена сосредоточенной силой F = 4 кН, равномерно распределенными нагрузками p₁ = 1 кН/м и p₂ = 2 кН/м, моментом М = 2 кН_·м. Угол

= 60° (рисунок 11, а). Определить реакции опор.

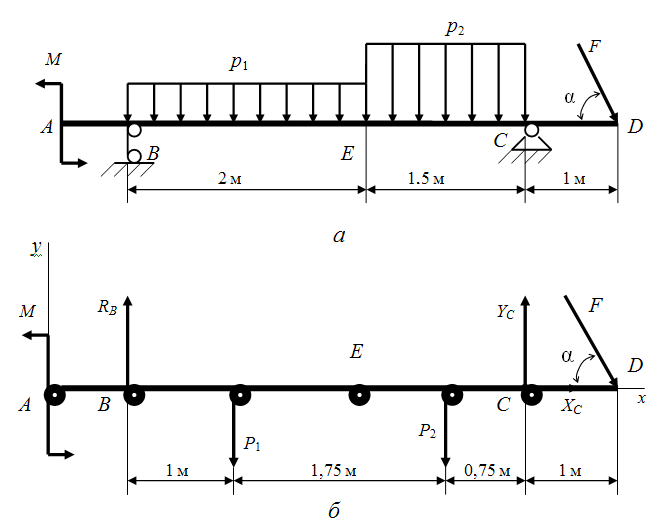
Рисунок 11 – Двухконсольная балка:

а – схема балки; б – схема действия сил

Заменим равномерно распределенные нагрузки равнодействующими сосредоточенными силами:

Р₁ = 1 кН/м _· 2 м = 2 кН; Р₂ = 2 кН/м _· 1,5 м = 3 кН.

Рассмотрим равновесие балки, на которую действуют активные нагрузки P_1, P₂, F, M. Отбросим связи, заменив их действие в шарнирно-подвижной опоре В одной вертикальной реакцией R_B, а в шарнирно-неподвижной опоре С двумя составляющими реакции X_C и Y_C (рисунок 11, б). При трех неизвестных задача статически определима.

Выберем положительные направления осей x и y. Составим уравнения равновесия:

(11)

(12)

(13)

Из уравнения (11)

Из уравнения (12)

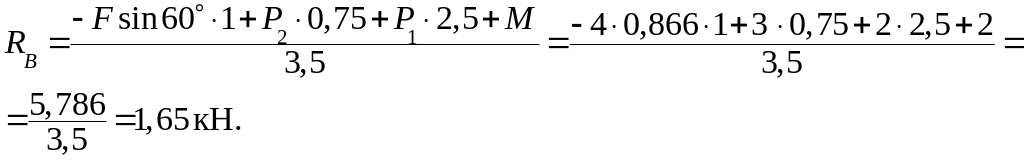
Из уравнения (13)

кН.

Следовательно, составляющая реакции Х_С направлена в противоположную сторону.

Модуль реакции в опоре С:

кН.

Направление реакции R_C :

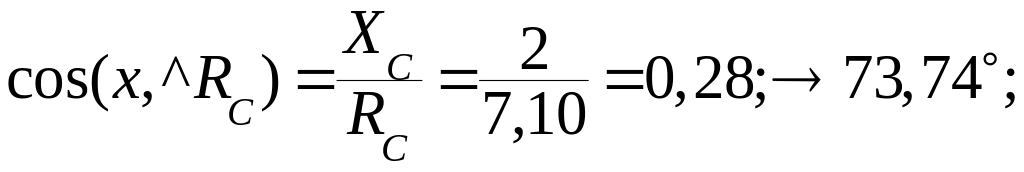
Учитывая направление составляющей реакции Х_С, определим:

- угол между осью x и R_C : 180 – 73.74 = 106,26°;

- угол между осью y и R_C равен 16,26°, в результате 106,26° – 16,26° = 90° (рисунок 12).

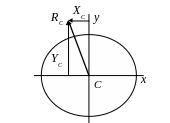
Рисунок 12 – Направление реакции в опоре С

Задание 4

Аналитически на основании уравнений равновесия определить реакции в опорах балочных конструкций, нагруженных различными активными силами. Предварительно упростить системы сил, определив равнодействующую равномерно распределенной нагрузки и точку приложения линии ее действия. Выяснить типы опор и возможные направления их реакций. Конструктивные схемы балок приведены в таблице 6, численные данные к заданию приведены в таблице 7.

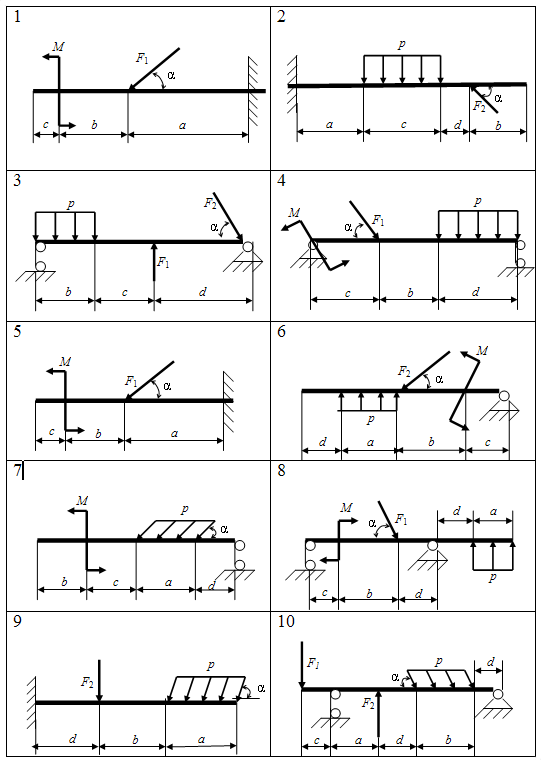
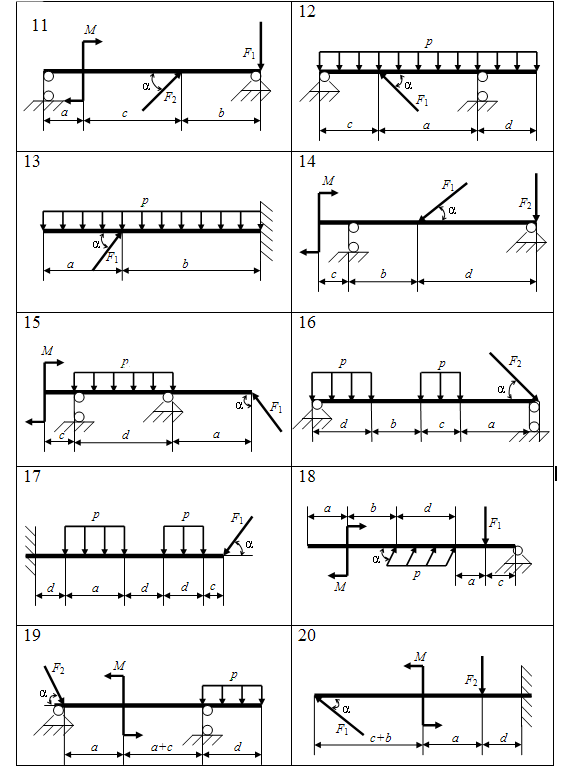
Таблица 6 – Схемы балок

П

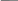
родолжение таблицы 6

О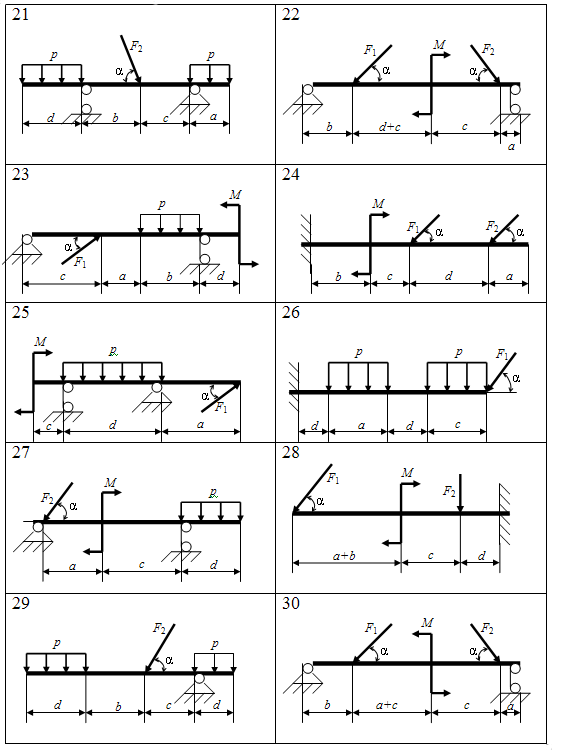 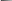кончание таблицы 6

Таблица 7 –Исходные данные для задания 4

Номер схемы	F1, кН	F2, кН	p, кН/м	M, кН·м	a, м	b, м	c, м	d, м	, град.
1	6	-	-	4	2	3	5	-	40
2	-	12	6	-	3	2	4	2	65
3	14	7	4	-	-	4	3	4	35
4	10	-	6	15	-	5	2	3	50
5	8	-	-	12	6	4	3	-	60
6	-	10	5	6	4	5	2	3	15
7	-	-	12	8	2	4	3	1	45
8	7	-	3	7	1	3	2	4	55
9	-	14	2	-	3	4	-	3	20
10	9	6	7	5	4	3	2	4	35
11	5	8	-	6	3	2	4	-	30
12	7	-	8	-	4	-	3	2	25
13	11	-	5	-	5	7	-	-	45
14	12	5	-	9	-	3	2	4	10
15	4	-	3	10	2	-	3	4	70
16	-	11	9	-	3	4	2	2	75
17	15	-	6	-	5	-	3	2	20
18	16	-	7	14	2	4	3	2	35
19	-	6	5	7	5	-	2	3	30
20	12	6	-	8	2	4	3	1	50
21	-	12	8	-	2	3	4	2	65
22	10	14	-	11	3	5	4	2	70
23	16	-	11	14	1	3	5	2	25
24	9	12	-	6	2	4	3	1	45
25	16	-	9	15	4	-	5	3	75
26	17	-	4	-	3	-	2	4	80
27	-	18	12	6	5	-	2	3	20
28	8	12	-	10	2	5	3	2	35
29	-	16	10	-	-	2	4	3	55
30	8	14	-	8	3	5	4	-	60