ДЕПАРТАМЕНТ ПО АВИАЦИИ

МИНИСТЕРСТВА ТРАНСПОРТА И КОММУНИКАЦИЙ

РЕСПУБЛИКИ БЕЛАРУСЬ

Минский государственный высший авиационный колледж

А. Н. ШИНКЕВИЧ

Теоретическая механика

С Т А Т И К А

Методическое пособие

к практическим занятиям

Минск

2012

УДК 531 (075. 8)

ББК 22. 21

Ш 62

Р е ц е н з е н т

А. Н. ОРДА

заведующий кафедрой «Теоретическая механика, теория механизмов и машин» Белорусского государственного аграрного технического университета, доктор технических наук, профессор

Одобрено и рекомендовано к изданию

Научно-методическим советом МГВАК

(протокол от 27 января 2012 года № 4)

Ш 62 Шинкевич, А. Н.

Теоретическая механика. Статика: методическое пособие к практическим

занятиям / А. Н. Шинкевич. – Минск: МГВАК, 2012. – 60 с.

Методическое пособие составлено в соответствии с типовой программой дисциплины «Теоретическая механика». В нем представлены краткие теоретические сведения, примеры решения задач и задания для самостоятельных и контрольных работ по разделу «Статика».

Предназначено для курсантов (студентов) специальностей «Техническая эксплуатация воздушных судов и двигателей» и «Техническая эксплуатация средств наземного обеспечения полетов».

© Мгвак, 2012

В В Е Д Е Н И Е

Теоретическая механика – наука, которая занимается изучением законов о механическом движении (перемещении) или равновесии физических тел.

Специалист гражданской авиации должен умело и рационально использовать современную быстроразвивающуюся технику. Наряду с практическими навыками управления и обслуживания воздушных судов он должен обладать широким техническим кругозором, в том числе знанием основ теоретической механики, которая не только позволяет объяснять явления окружающего мира, но и служит научным фундаментом для многих технических дисциплин.

Учебная дисциплина «Теоретическая механика» – основа общетехнической подготовки инженеров. Главная задача теоретической механики – подготовка современного специалиста, обладающего знаниями, умениями и навыками в области расчета и рационального проектирования элементов конструкции с обеспечением их надежности и работоспособности.

Курс «Теоретическая механика» состоит из трех тематических разделов: «Статика», «Кинематика», «Динамика».

В настоящем методическом пособии рассматриваются методы решения задач первого раздела теоретической механики – статики, изучающей вопросы равновесия материальных тел под действием различных систем сил.

Плоская система сходящихся сил

Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.

Для определения равнодействующей системы сходящихся сил часто используют графический метод – геометрическое сложение векторов, составляющих систему сил.

Вторым методом решения задач на сходящуюся систему сил является составление уравнений равновесия проекций сил на координатные оси x и y двухкоординатной системы.

Пример 1. Сходящиеся силы в полете воздушного судна

Самолет при наборе высоты, горизонтальном полете или снижении движется прямолинейно и равномерно под углом к горизонту. Вес самолета – G. Сила тяги двигателей F_g составляет угол с направлением полета (рисунок 1).

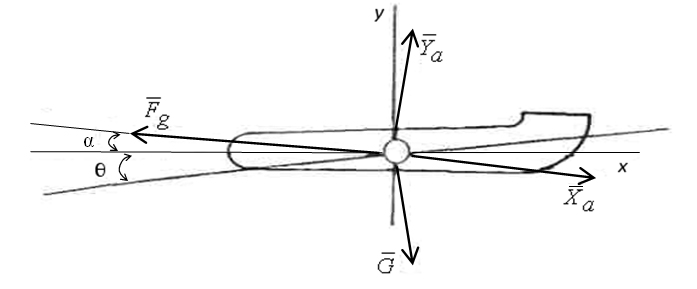
Рисунок 1 – Сходящиеся силы, приложенные к самолету

Определить графически равнодействующую аэродинамических сил и и аналитически с помощью уравнений равновесия системы сходящихся сил , , , (как равнодействующую сил и ).

Для схемы, указанной на рисунке 1, исходные данные: G = 500 кН; = 150 кН; = 0^⁰; = 6^⁰. Выполним упрощенный рисунок самолета в соответствии с исходными данными. Так как угол к горизонту = 0^⁰, то направление веса G совпадает с вертикальной осью y (рисунок 2).

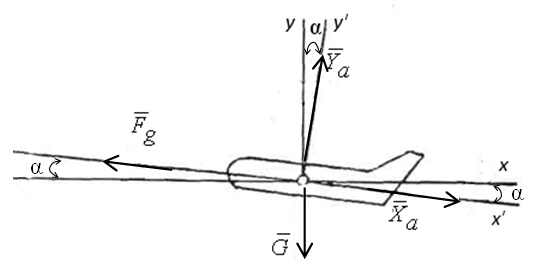
Рисунок 2 – Пример сходящихся сил для самолета

Графический метод решения

Проведем вектор с масштабным коэффициентом сил (например, = 10 кН/мм), от его конца проведем вектор в том же масштабе и в соответствии с направлением этого вектора. В условиях равновесия проведем замыкающий вектор (рисунок 3).

Направление вектора составляет примерно 75° к линии горизонта, а его модуль нужно определить измерением вектора с

учетом масштабного коэффициента сил :

R = 53 мм _· = 53 _· 10 = 530 кН.

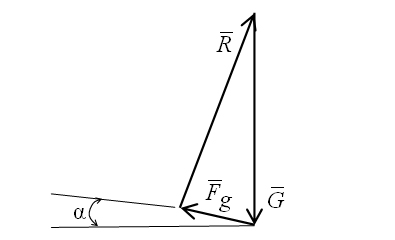
Рисунок 3 – Графическое решение примера 1

Аналитический метод решения

Для аналитического решения составим уравнения равновесия, предварительно проведя новые координатные оси x' и y', совпадающие по направлениям с векторами , , (см. рисунок 2):

(1)

(2)

Из уравнения (1) определим значение силы лобового сопротивления:

кН.

Из уравнения (2) определим значение подъёмной силы:

кН.

Равнодействующая аэродинамических сил

кН.

Несовпадение результатов графического и аналитического

решений составляет 1,27 %, что вполне приемлемо.

Задание 1

По условию примера 1 и в соответствии с рисунком 1 построить схему действия сил на самолет аналогично рисунку 2. Определить равнодействующую R графическим методом (см. рисунок 3), а также равнодействующую R, силу лобового сопротивления X_a и подъемную силу Y_a аналитическим методом. Сравнить результаты решений. Варианты исходных данных приведены в таблице 1 (отрицательные значения углов откладываются в направлении, противоположном указанному на рисунке 1).

Таблица 1 – Исходные данные для задания 1

Номер варианта	, град.	, град.	, кН	, кН	Номер варианта	, град.	, град.	, кН	, кН
1	6	2	53	13	16	10	2	430	100
2	5	3	200	44	17	-3	-1	1100	300
3	8	4	150	36	18	-5	-3	950	270
4	6	8	220	48	19	10	5	460	120
5	5	3	210	47	20	-3	-4	1300	340
6	8	2	60	15	21	-5	-2	900	220
7	6	4	60	15	22	10	-1	1000	290
8	5	2	350	90	23	10	6	450	115
9	8	2	160	38	24	-3	8	880	260
10	6	6	400	125	25	-5	-5	1150	310
11	5	5	560	140	26	10	-2	480	130
12	8	8	610	155	27	-3	-1	1200	320
13	6	-2	45	10	28	-5	8	1300	360
14	5	2	220	50	29	10	3	400	120
15	8	-1	170	40	30	-3	2	55	14

Пример 2. Расчет стержневой системы

Для шарнирно-стержневой конструкции ABC, нагруженной в шарнире B, определить усилия в стержнях 1 и 2 (рисунок 4).

Рисунок 4 – Шарнирно-стержневая система

Исходные данные: ; ; F₁ =100 кН; F₂ =75 кН.

Решаем задачу двумя методами.

Графический метод решения

Определим масштабный коэффициент сил применительно к силе F₁:

= 1 кН/мм.

Построим многоугольник сил, первоначально направляя усилия в стержнях 1 и 2 (S₁ и S₂) от узла В. В условиях равновесия многоугольник сил должен быть замкнут. Сила F₂ направлена вдоль гибкого троса, переброшенного через блок. Отметим точку В, из которой проведем вертикально вниз вектор длиной 100 мм. В соответствии с направлением действия вектора построим его длиной

Векторы и известны только по направлению. Проведем их, замыкая в условиях равновесия многоугольник сил. Следует внимательно определять углы, под которыми векторы сил располагаются друг к другу (рисунок 5).

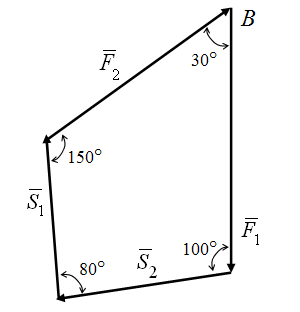
Рисунок 5 – Графическое решение примера

Измерим линейкой неизвестные усилия S₁ и S₂ и через масштабный коэффициент сил вычислим искомые усилия:

· 1 кН;

кН.

Заметим, что линейные измерения с помощью обычной миллиметровой линейки производятся с точностью не выше 0,5 мм.

Аналитический метод решения

П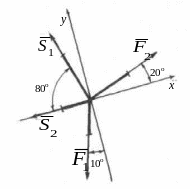 риняв точку В за начало координат, выберем положение осей x и y. Логично провести одну из осей координат так, чтобы она совпадала с линией действия неизвестной силы, тогда последняя будет проецироваться на ось в натуральную величину. Совместим ось x с осью стержня 2 (рисунок 6).

0

Рисунок 6 – Аналитический расчет примера 2

Ось y перпендикулярна оси x. Найдем углы наклона сил к координатным осям. Составим уравнения равновесия для плоской системы сходящихся сил:

(3)

(4)

Из уравнения (4)

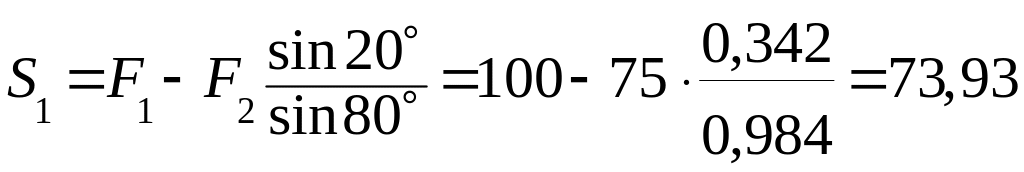кН.

Из уравнения (3)

кН.

Разница усилий в графическом и аналитическом решениях составляет доли процента (0,1 и 0,4 % соответственно).

Задание 2

По схеме рисунка 4 и численным данным таблицы 2 графически и аналитически определить усилия в стержнях.

Таблица 2 – Исходные данные для задания 2

Номер варианта	, град.	, град.	F1, кН	F2, кН	Номер варианта	, град.	, град.	F1, кН	F2, кН
1	50	40	100	90	16	80	70	100	60
2	40	30	140	80	17	80	60	80	70
3	50	20	120	100	18	70	50	90	80
4	60	10	100	90	19	60	40	100	90
5	70	10	90	80	20	50	30	120	100
6	80	20	80	70	21	40	20	110	100
7	80	30	100	70	22	50	20	140	100
8	70	40	110	80	23	50	30	140	90
9	60	50	120	90	24	60	30	100	80
10	50	30	140	100	25	70	40	100	70
11	40	30	120	100	26	80	60	110	60
12	40	20	140	90	27	80	45	120	100
13	50	40	120	80	28	70	30	120	90
14	60	50	120	70	29	60	30	100	80
15	70	60	110	60	30	50	30	90	70